结对项目

1.Github项目地址：https://github.com/he0ry/couple

项目合作者：黄华3118005050李洋3118005057

2. PSP2.1表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60	90
· Estimate	· 估计这个任务需要多少时间	60	90
Development	开发	2200	2230
· Analysis	· 需求分析 (包括学习新技术)	300	300
· Design Spec	· 生成设计文档	60	60
· Design Review	· 设计复审 (和同事审核设计文档)	30	60
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	30
· Design	· 具体设计	120	120
· Coding	· 具体编码	1000	1000
· Code Review	· 代码复审	180	180
· Test	· 测试（自我测试，修改代码，提交修改）	480	480
Reporting	报告	70	70
· Test Report	· 测试报告	45	45
· Size Measurement	· 计算工作量	15	15
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	10	10
合计		2330	2390

 

4.设计实现过程

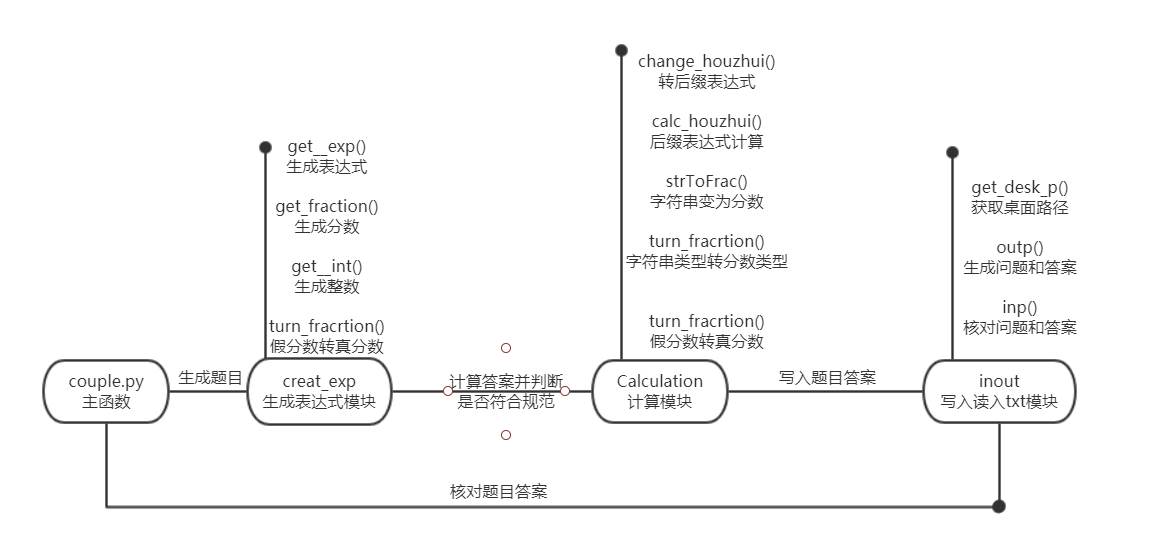
5.代码说明

生成表达式模块：随机生成分数和整数，随机插入括号，并将假分数转真分数，最后生成str表达式。

from fractions import Fraction
import random
# 生成表达式
def get__exp(subject__num,area):
    expression = ''
    bracket = 0
    operator_num = random.randint(1, 3)  # 生成运算符数
    if operator_num != 1:  #操作数大于1
        bracket = random.choice([1,2])  #随机选择是否插入括号
        if bracket == 1:
            #在第几个数插入括号
            breaket__num1 = random.randint(0,operator_num - 1)
            if breaket__num1 == 0:
                breaket__num2 = random.randint(breaket__num1 + 1,operator_num - 1)
            else:
                breaket__num2 = random.randint(breaket__num1 + 1,operator_num)
    for i in range(2*operator_num+1):
        if i % 2 == 0:
            if random.randint(1,4) == 1:
                num = str(get_fraction(area))  #生成分数
            else:
                num = str(get__int(area))  #生成整数
            if bracket == 1:  
                if i == breaket__num1 * 2:  #插入左括号
                    num = '( ' + num 
                elif i == breaket__num2 * 2:
                    num = num + ' )'   #插入右括号
                    bracket = 0
            expression += ' ' + num   #表达式加入数或括号
        else:
            op = str(random.choice(['+','-','×','÷']))  # 随机选择运算符 (+ - × /)
            expression += ' ' + op   #表达式加入运算符
    return expression 

# 生成分数
def get_fraction(area):   
    while True:
        mum = random.randint(1, area)
        son = random.randint(1, mum*area)
        n = Fraction(son,mum)
        if '/' in str(n):
            if n > 1:
                return turn_fracrtion(n)
            return n

# 生成整数
def get__int(area):
    return random.randint(1,area)

 # 假分数转真分数
def turn_fracrtion(results): 
    return str(int(results)) + "'" + str(results - int(results))

计算模块：将str表达式转为中缀表达式再转为后缀表达式进行计算

from fractions import Fraction

def get__result(exp):
    return calc_houzhui(change_houzhui(exp))

# 转为后缀表达式
def change_houzhui(exp):
    result = []  # 结果列表
    stack = []  # 栈
    exp_list = exp.split(' ')
    for item in exp_list:
        if item.isnumeric() or '/' in item or '\'' in item:  # 如果当前字符为数字那么直接放入结果列表
            result.append(item)
        else:  # 如果当前字符为一切其他操作符
            if len(stack) == 0:  # 如果栈空，直接入栈
                stack.append(item)
            elif item in '×÷(':  # 如果当前字符为×÷（，直接入栈
                stack.append(item)
            elif item == ')':  # 如果右括号则全部弹出（碰到左括号停止）
                t = stack.pop()
                while t != '(':
                    result.append(t)
                    t = stack.pop()
            # 如果当前字符为加减且栈顶为乘除，则开始弹出
            elif item in '+-' and stack[-1] in '×÷':
                if stack.count('(') == 0:  # 如果没有左括号，弹出所有
                    while stack:
                        result.append(stack.pop())
                else:  # 如果有左括号，弹到左括号为止
                    t = stack.pop()
                    while t != '(':
                        result.append(t)
                        t = stack.pop()
                    stack.append('(')
                stack.append(item)  # 弹出操作完成后将‘+-’入栈
            else:
                stack.append(item)  # 其余情况直接入栈（如当前字符为+，栈顶为+-）
    # 表达式遍历完了，但是栈中还有操作符不满足弹出条件，把栈中的东西全部弹出
    while stack:
        result.append(stack.pop())
    # 返回中缀表达式数字与符号分离列表
    return result

#后缀表达式计算
def calc_houzhui(exp_list):
    num = []
    base_opt = ['+', '-', '×', '÷']
    for i in exp_list:
        if i.isnumeric():
            num.append(int(j))
        elif '/' in j or '\'' in j:
            num.append(strToFrac(j))
        if i in base_opt:
            num2 = num.pop()
            num1 = num.pop()
            if i == "+":
                num.append(num1 + num2)
            elif i == "-":
                num.append(num1 - num2)
                if num[-1] < 0:
                    return -1
            elif i == "×":
                num.append(num1 * num2)
            else:  
                if num2 == 0:
                    return -1 
                else:
                    num.append(Fraction(num1,num2))
    if num[0] > 1 and '/' in str(num[0]):
        return turn_fracrtion(num[0])
    return num[0]

#字符串变为分数
def strToFrac(string):
    #如果是带分数
    if '\'' in string:
        withFrac = string.split('\'')
        INT = int(withFrac[0])  #整数部分
        son = int((withFrac[1].split('/'))[0])  #分子部分
        mum =int((withFrac[1].split('/'))[1])  #分母部分
        return Fraction((INT*mum+son),mum)
    #如果是普通真分数
    elif '/' in string:
        son = int((string.split('/'))[0])
        mum = int((string.split('/'))[1])
        return Fraction(son,mum)
    #如果是整数
    else :
        return Fraction(int(string),1) 

 # 假分数转真分数
def turn_fracrtion(results): 
    return str(int(results)) + "'" + str(results - int(results))

读写模块：将表达式及答案写入txt，并有读取答案比对答案获取得分情况功能

import os
import Calculation
import Create__exp
import datetime

#获取桌面路径
def get_desk_p():
    return os.path.join(os.path.expanduser('~'),"Desktop")

#生成问题和答案
def outp(subject__num,area):
    #生成的时间
    now = datetime.datetime.now()  
    file__time = now.time().__format__('%H.%M.%S')
    expfile = r''+get_desk_p() + r'\exercise' + file__time + '.txt'  #问题路径
    ansfile = r''+get_desk_p() + r'\answer' + file__time + '.txt'   #答案路径
    user_ansfile = r''+get_desk_p()+ r'\useranswer' + file__time + '.txt'  #用户答案路径
    with open(r''+expfile,'w') as f1, \
        open(r''+ansfile,'w') as f2:
        a = 0
        while(a < subject__num):
            expression = Create__exp.get__exp(subject__num,area)  #生成表达式
            result = Calculation.get__result(expression)  #计算答案
            if result == -1:
                continue
            f1.write(str(a+1) + '.' + expression + ' = ' + '\n')  #写入问题
            f2.write(str(a+1) + '.' + str(result) + '\n')   #写入答案
            a += 1 
    f = open(r''+ user_ansfile,'w')
    f.close()
    print('你的题目已生成\n在桌面' + r'\exercise' + file__time + '.txt')
    print('你的答案已生成\n在桌面' + r'\answer' + file__time + '.txt')
    print('请到桌面' + r'\useranswer' + file__time + '.txt' + '答题')

# 核对答案
def inp(user_answerspath,Answerspath):
    right__num = wrong__num = 0  
    right__sign = []
    wrong__sign = []
    tag = 1  #记录题号变量
    #核对答案的时间
    now = datetime.datetime.now() 
    file__time = now.time().__format__('%H.%M.%S')
    gradepath = r''+get_desk_p() + r'\grade' + file__time + '.txt'  #得分情况路径
    with open(r''+ user_answerspath,'r') as f1,\
        open(r''+ Answerspath,'r') as f2:
        for line1,line2 in zip(f1.readlines(),f2.readlines()):
            if line1.split() == line2.split():
                right__num += 1
                right__sign.append(tag)
            else:
                wrong__num += 1
                wrong__sign.append(tag)
            tag += 1
    #写入得分情况
    with open(r''+gradepath,'w') as f:
        f.write('正确数目' + str(right__num))
        f.write(str(right__sign))
        f.write('\n错误数目' + str(wrong__num))
        f.write(str(wrong__sign))
    print('你的得分情况已经放到桌面' + r'\grade' + file__time + '.txt')

6.测试运行

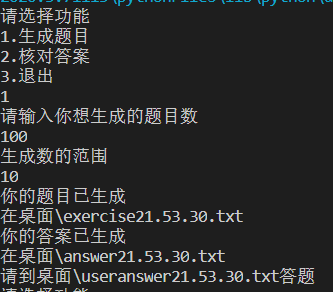
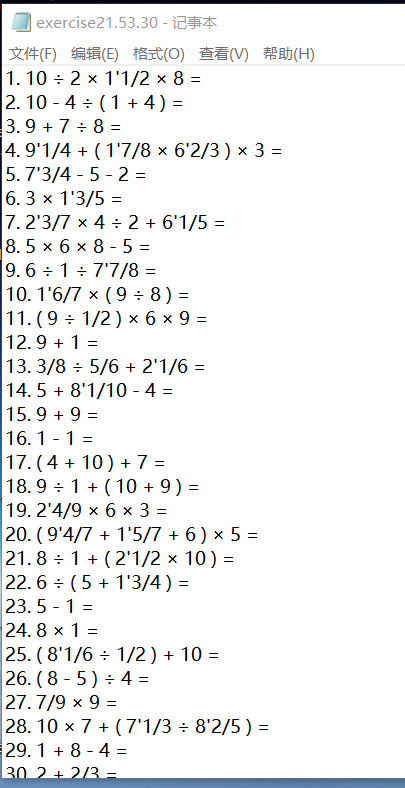
2、选择功能2核对答案并活得得分情况

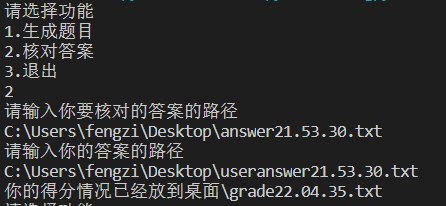
7.项目小结：

在开发初期计划分三个模块，生成表达式、计算、写入读取，到开发中期的时候上网查资料的时候发现可以用二叉树来生成表达式，计算并查重这种高效的方法，可以使计算效率大大提高，但重头再来的代价太大，通过这次项目我们意识到自己解决问题的能力与方法有待提高，优秀的算法与数据结构可以使程序运行效率大大提高。

此次项目采用结对编程，我们认为最大的好处在于解决问题的效率可以大大提高，因为两个人思考解决方案与上网查资料都比一个人更快，而且两个人干活更有活力不容易累。