excrt

“为什么先讲excrt？因为excrt和crt没有任何关系。”

好吧实际上确实如此

中国剩余定理可求解如下的方程组

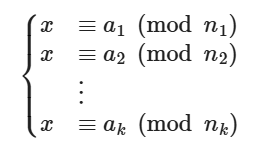
但如果n之间不互质它就失效了

此时就需要可爱的excrt来求解啦

至于大体过程。。我懒得写了

这是从oi-wiki上偷的 我感觉写的已经比较清楚了 奈何我实在太菜 所以中间有个地方还瞪了挺久 代码实现也没有

不然我也懒得写博客

一点补充

对于前面的两个方程组的解的转化 oi-wiki跳的实在有点快

设特解为x0 则通解为x0-klcm(m1,m2) 注意到等价于x≡x0(mod lcm(m1,m2))

详细证明可以去看这里 不过我是懒得大晚上看这么详细的证明的

多个方程合并流程

每次我们取出两个方程 将他们按上述原理合成一个方程 这样不断合并直到只剩一个方程 再求解就好了

点击查看代码

int excrt() {
	int x,y;
	int b=yu[1],M=mo[1];//b表示合并前i-1方程的特解（余数） M为lcm(前i-1的模数) 
	for(int i=2;i<=n;i++) {
		int d=exgcd(mod,mo[i],x,y);//最大公约数 
		int s=((yu[i]-b)%mo[i]+mo[i])%mo[i];//等式右边 
		if(s%d!=0) {   //裴蜀定理判无解 
			cout<<-1;
			return 0;
		}
		x=qm(x,s/d,mo[i]);  //防止爆longlong 用int128也可以 
		b+=x*M; //更新b 
		M=(m[i]/d)*M; //更新M 
		b=(b%M+M)%M; //取模 
	}
	return (b%M+M)%M;
}