图的存储
- 图的定义:
图 G 是由两个集合顶点集 V(G) 和边集 E(G) 组成的,记作G=( V(G),E(G) ),简称G=(V,E)。V是顶点的有穷非空集合,E是两个顶点之间的关系——边的有穷集合。
有时对图的边或弧赋予相关的数值,这种与图的边或弧相关的数值叫做权。
这些权可以表示从一个顶点到另一个顶点的距离。可以表示从一个顶点到另一个顶点的耗费。
- 顶点的度
顶点的度:即与该顶点相关联的边的条数。在有向图中,指向该顶点的边的条数称之为入度,而从该顶点指出来的边的条数称之为该顶点的出度,而该顶点的度数为入度和出度之和。
- 连通
在无向图中:
如果从顶点v到顶点v'有路径,则称v和v'之间是连通的。如果图G中的任意连个顶点都是连通的,那么称这个图为连通图。
对于无向图,在非连通图中连通分量是指该图中最大连通子图。
在有向图中:
如果从顶点v到顶点v'有路径,并且从v'到v之间也有路径,则说明v和v'之间是连通的。如果一个有向图中,任意选取两个顶点,都是连通的,则称这个图为强连通图。
对于有向图,在非连通图中强连通分量是指该图中最大连强通子图。
- 图的存储结构
- 邻接矩阵:
邻接矩阵存放 n 个顶点信息和 n2 条边或弧信息。其每一个元素 aij 定义为:
非带权图
带权图(Wij表示权重)
例有向图 G:
(习惯性的会给图中每一个节点标号,标号从1开始。)其邻接矩阵为:
有向图的邻接矩阵不是对称矩阵。
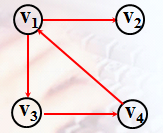
无向图:
其邻接矩阵为:
无向图的邻接矩阵是对称矩阵。
邻接矩阵的优点:
1. 容易判断任意两个顶点之间是否有边或弧。
2. 容易求取各个顶点的度。
- 邻接表和逆邻接表
对图中每一个顶点建立一个单链表,指示与该顶点关联的边或出弧。
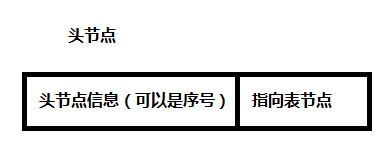
头节点存储结构(存储顶点信息):
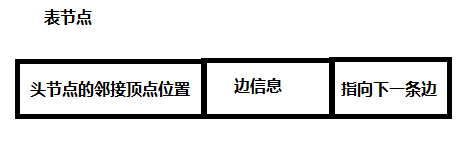
表节点存储结构(存储边信息):
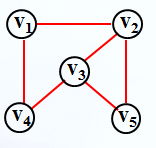
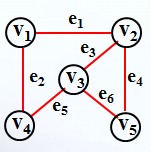
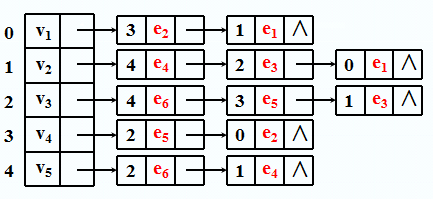
对于无向图:
对应邻接表:
一般所有的头节点会定义成一个数组。
所需存储空间:n + 2e。
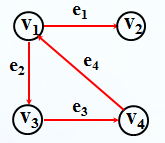
而对于有向图:
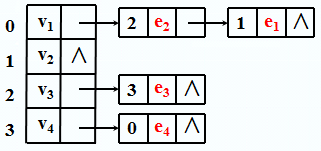
对应邻接表(存储所有顶点的入度信息):
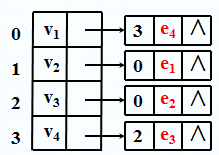
对应逆邻接表(存储所有顶点的出度信息):
存储空间:2n+2e。
邻接表和邻接矩阵的比较:
比较省存储空间的是邻接表,求两个顶点是否连通更方便的是邻接矩阵(邻接矩阵直接查找aij是否为0或者无穷大,而邻接表要做一个线性查找)。
- 十字链表
针对有向图,为了更好的存储信息和节省空间,采取十字链表的方法。
十字链表头节点存储结构:
十字链表表节点存储结构:
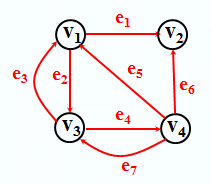
例如:
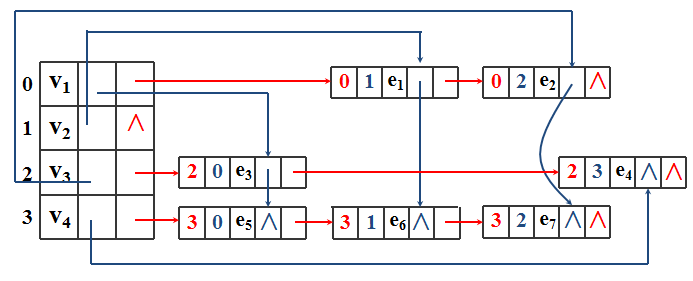
对应的十字链表:





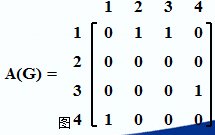




 浙公网安备 33010602011771号
浙公网安备 33010602011771号