【每周例题】力扣 C++ 组合

组合

题目

力扣 组合

 题目解析

1.我们可以根据题目分析可知，题目所要求我们做的是：从1到n进行遍历，找出k个数组成小组合，再将小组合拼接在一起成为大组合输出。

2.所以，根据题目，我们可以采用两个数组，一个一维数组temp，负责存储k个数，组为小组合，一个二维数组res，存储小组合，变为大组合。

下面为图解：

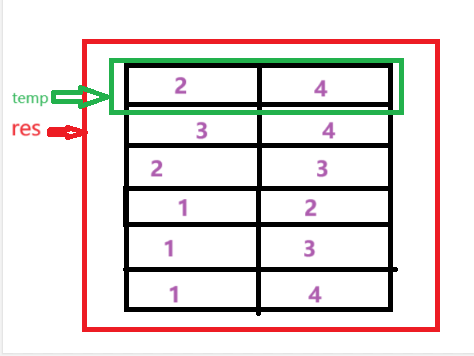
 3.这道题动用了回溯法（有递归即会出现回溯），想要了解的可以点击下面的链接：

回溯法

4.这题可以动用容器，我们可以把容器看为一个动态扩展的数组，想要了解容器的可以点击下面链接：

容器

代码：

#include<iostream>
#include<vector>
using namespace std;

class Solution 
{
    vector<vector<int>> res;//二维数组
    vector<int> temp;//一位数组 保存临时组合
public:
    void recursion(int i, int n, int k)//从i遍历到n，寻找长度为k的数组
    {
        if (temp.size() == k)
        {
            res.push_back(temp);//将当前组合添加到res
        }
        else if (i <= n)
        {
            temp.push_back(i);//在容器后添加一个元素
            recursion(i + 1, n, k);
            temp.pop_back();//删除添加的尾元素
            recursion(i + 1, n, k);
        }
    }

    vector<vector<int>> combine(int n, int k)
    {
        recursion(1, n, k);
        return res;
    }
};

代码调试解析：

想要理解上面的代码，可以运行下面的代码，必要时可以打断点进行调试：

#include <iostream>  
#include <vector>  

using namespace std;

class Solution {
public:
    vector<vector<int>> combine(int n, int k) {
        recursion(1, n, k);
        return res;
    }

private:
    vector<vector<int>> res; // 存储所有组合的结果  
    vector<int> temp; // 存储当前组合  

    void recursion(int i, int n, int k) {
        // 打印当前递归的状态  
        cout << "递归调用: i = " << i << ", n = " << n << ", k = " << k << ", 当前组合: ";
        for (int num : temp) {
            cout << num << " ";
        }
        cout << endl;

        // 如果当前组合的长度等于k，则将其添加到结果中  
        if (temp.size() == k) {
            res.push_back(temp);
            // 打印找到的组合  
            cout << "找到一个组合: ";
            for (int num : temp) {
                cout << num << " ";
            }
            cout << endl;
            return; // 返回，避免进一步递归  
        }

        // 如果还有数字可以加入组合，则继续递归  
        if (i <= n) {
            // 尝试将当前数字i加入组合  
            temp.push_back(i);
            // 递归调用，尝试加入下一个数字  
            recursion(i + 1, n, k);
            // 移除当前数字i，尝试不加入它的情况  
            temp.pop_back();

            // 如果当前数字i不加入组合，则直接尝试下一个数字  
            // 注意：这里的递归调用不应该再次尝试加入当前数字i，因为我们已经尝试过  
            // 所以这里的调用应该与上一个调用使用相同的i值  
            recursion(i + 1, n, k);
        }
    }
};

int main() {
    Solution solution;
    int n = 4;
    int k = 2;
    vector<vector<int>> combinations = solution.combine(n, k);

    // 打印所有组合  
    cout << "所有组合:" << endl;
    for (const auto& combination : combinations) {
        for (int num : combination) {
            cout << num << " ";
        }
        cout << endl;
    }

    return 0;
}