【暑假题目】10230708 矩阵旋转

矩阵旋转

题目

请使用C++，原地90℃旋转一个M*N的矩阵，不允许增加任何内存空间（空间复杂度为O(1)）

题目分析

题目可以注意以下几点：

（1）90度旋转矩阵

（2）矩阵为M*N矩阵，即M,N可能相等，也可能不相等

（3）不允许增加内存空间，空间复杂度为O(1)

思路分析及其代码实现

思路

我们可以先从M、N相等的矩阵开始入手寻找规律

 

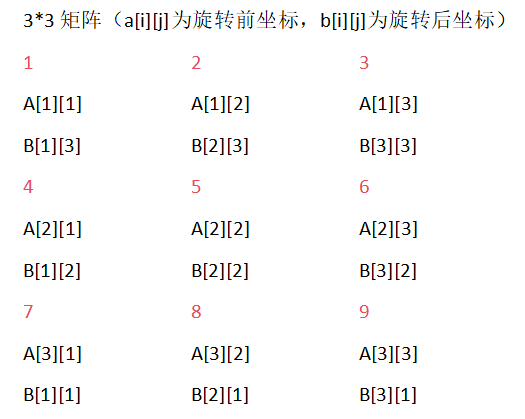
 由以上矩阵做观察，我们发现对于方阵我们有三种方法进行旋转：

（1）将方阵分为好几个圈，从最外圈开始旋转，此时可以通过双重for循环进行矩阵的坐标旋转，第一层for循环控制列数，第二重for循环控制行数

（2）我们首先以对角线为界，进行第一次翻转，然后以中轴线为界进行第二次翻转（该方法对奇数方阵使用比较好）

（3）将方阵转化为转置矩阵，然后再进行左右翻转。

接下来我们观察M，N不相等的矩阵继续寻找规律

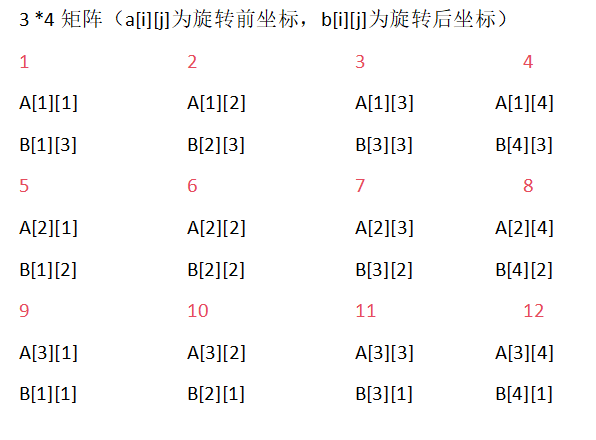
我们发现，对于M,N不相等的矩阵，上面的第一种和第二种方法执行起来都比方阵要麻烦，而第三种不如直接观察坐标的规律直接输出简便

 代码一

直接观察坐标后输出旋转后的矩阵

//首先。我们默认矩阵中的数字，用户是从左到右，从上到下进行赋值
#include<iostream>
using namespace std;
int main()
{
	int m, n;//矩阵规格
	int a[1000][1000];
	int i, j;
	cout << "请输入你所需要旋转90度的原矩阵规格(M*N)" << endl;
	cin >> m >> n;
	cout << "请按照从左到右，从上到下的顺序输入矩阵中的数" << endl;
	for (i = 0; i < m; i++)
	{
		for (j = 0; j < n; j++)
		{
			cin >> a[i][j];//输入数字
		}
	}
	cout << "以下显示的是旋转前的矩阵" << endl;
	for (i = 0; i < m; i++)
	{
		for (j = 0; j < n; j++)
		{
			cout << a[i][j] << ' ';
		}
		cout << endl;
	}
	cout << "以下显示的是旋转后的矩阵" << endl;
	for (j = 0; j < n; j++)
	{
		for (i = m - 1; i >= 0; i--)
		{
			cout << a[i][j] << ' ';
		}
		cout << endl;
	}
	return 0;
}

　结果一

   

 代码二

以方阵为例，使用方法二

//首先。我们默认矩阵中的数字，用户是从左到右，从上到下进行赋值
#include<iostream>
using namespace std;
int main()
{
	int m;//矩阵规格
	int a[1000][1000];
	int i, j;
	cout << "请输入你所需要旋转90度的原矩阵规格(M*M)" << endl;
	cin >> m;
	cout << "请按照从左到右，从上到下的顺序输入矩阵中的数" << endl;
	for (i = 0; i < m; i++)
	{
		for (j = 0; j < m; j++)
		{
			cin >> a[i][j];//输入数字
		}
	}
	cout << "以下显示的是旋转前的矩阵" << endl;
	for (i = 0; i < m; i++)
	{
		for (j = 0; j < m; j++)
		{
			cout << a[i][j] << ' ';
		}
		cout << endl;
	}
	cout << "以下显示的是旋转后的矩阵" << endl;
	//水平翻转
	for (i = 0; i < m / 2; i++)
	{
		for (j = 0; j < m; j++)
		{
			swap(a[i][j], a[m - i - 1][j]);//交换函数
		}
	}
	//对角线翻转
	for (i = 0; i < m; i++)
	{
		for (j = 0; j < i; j++)
		{
			swap(a[i][j], a[j][i]);
		}
	}
	for (i = 0; i < m; i++)
	{
		for (j = 0; j < m; j++)
		{
			cout << a[i][j] << " ";
		}
		cout << endl;
	}
	return 0;
}

结果二

 寻找更简单的解法ing