算法笔记（6）

题目1(lc204)

给定整数 n ，返回所有小于非负整数 n 的质数的数量。

示例 1：
输入：n = 10
输出：4
解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

示例 2：
输入：n = 0
输出：0

示例 3：
输入：n = 1
输出：0

思路

准备一个长度为n的bool类型数组，表示下标对应数字是否是不质数，设为true就代表不是。如果x不是素数，那么2*x、3*x、4*x......都不是质数。基于这种原理把bool类型数组中对应自己的位置设置为true。

代码

int countPrimes(int n) 
{
    if (n < 3)
    {
        return 0;
    }
    vector<bool> isNotPrime(n);
    int count = n / 2;
    for (int i = 3; i * i < n; i += 2)
    {
        if (isNotPrime[i])
        {
            continue;
        }
        for (int j = i * i; j < n; j += 2 * i)
        {
            if (!isNotPrime[j])
            {
                --count;
                isNotPrime[j] = true;
            }
        }
    }
    return count;
}

题目2(lc190)

颠倒给定的 32 位无符号整数的二进制位。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在示例 2 中，输入表示有符号整数 -3，输出表示有符号整数 -1073741825。

示例 1：
输入：n = 00000010100101000001111010011100
输出：964176192 (00111001011110000010100101000000)
解释：输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

示例 2：
输入：n = 11111111111111111111111111111101
输出：3221225471 (10111111111111111111111111111111)
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

思路

先交换前16位和后16位，前16位交换它的前8位和后8位，后16位也交换它的前8位和后8位。8位的交换它的前4位和后4位。4位的交换它的前2位和后2位。2位的交换它的前1位和后1位。实现逆序

代码

uint32_t reverseBits(uint32_t n) 
{
	n = (n >> 16) | (n << 16);
	n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8);
	n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4);
	n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2);
	n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1);
	return n;
}

题目3(lc172)

给定一个整数 n ，返回 n! 结果中尾随零的数量。

提示 n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1

示例 1：
输入：n = 3
输出：0
解释：3! = 6 ，不含尾随 0

示例 2：
输入：n = 5
输出：1
解释：5! = 120 ，有一个尾随 0

示例 3：
输入：n = 0
输出：0

思路

有多少个5因子和2因子配对。因为2的因子肯定比5多，所以只需要考虑有多少个5因子即可。
首先每5个数中有1个5因子，即 n = n/5
然后由于上一步的过滤，25里面还有一个5因子，即n = n/5
然后由于上一步的过滤，125里面又有一个5因子，即n = n/5
......
在n = 0之前把每一步的n累加即可

代码

int trailingZeroes(int n) 
{
    int ans = 0;
    while (n > 0)
    {
        n /= 5;
        ans += n;
    }
    return ans;
}

题目4(lc152)

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位整数。

子数组是数组的连续子序列。

示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

思路

动态规划，准备两个dp
max[i]含义：以i结尾的的情况下最大的乘积为多少。
min[i]含义：以i结尾的的情况下最小的乘积为多少。

max[i]有三种情况：

只取当前位置的值，即max[i] = arr[i]
前面最好的乘积乘现在位置，即max[i] = arr[i] * max[i - 1]
由于数组中有负数，负数乘以负数可以得到正数，所以还有一种可能性是当前位置的值乘以i-1结尾乘积最小的结果。即max[i] = arr[i] * min[i - 1]

max[i]的值在三种情况取最大值

min[i]有三种情况：

只取当前位置的值，即min[i] = arr[i]
前面最小的乘积乘现在位置，即min[i] = arr[i] * min[i - 1]
还有一种可能性是当前位置的值乘以i-1结尾乘积最大的结果(例如当前位置是负数，max[i - 1]为正数情况)。即min[i] = arr[i] * max[i - 1]

min[i]的值在三种情况取最小值

在更新的过程中抓取max[i]的最大值即可。

代码

int maxProduct(vector<int>& nums) 
{
    int ans = nums[0];
    int Max = nums[0];
    int Min = nums[0];
    for (int i = 1; i < nums.size(); i++)
    {
        int curMax = max(nums[i], max(Max * nums[i], Min * nums[i]));
        int curMin = min(nums[i], min(Min * nums[i], Max * nums[i]));
        ans = max(ans, curMax);
        Max = curMax;
        Min = curMin;
    }
    return ans;
}

题目5(lc73)

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

示例 1：

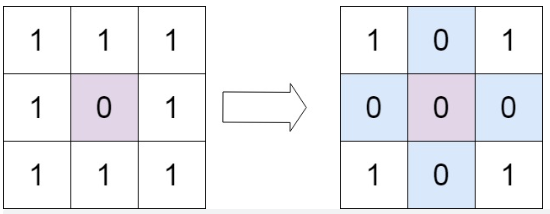
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

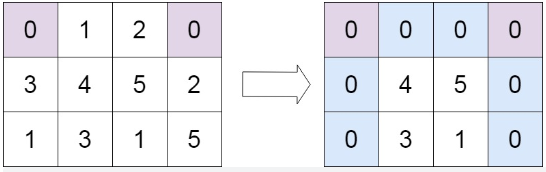
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

思路

利用矩阵的第0行和第0列储存信息来表示当前行和当前列是否在变换后全变成0，如果碰到dp[i][j] == 0，就把dp[i][0]和dp[0][j]置为0，代表i行和j列在变换后会全变成0，但是这样会产生歧义，如果dp[i][0]或dp[0][j]原来就是0，那么第0列或第0行也要全变成0，这样会造成信息的覆盖，所以我们准备两个变量，代表是否将第0列或第0行全变成0，如果dp[i][0]或dp[0][j]在修改之前就是0，那么在对应的变量标记上即可。再剩一点空间的做法是将dp[0][0]的位置作为其中一个变量，只准备一个变量。

代码

void setZeroes(vector<vector<int>>& matrix) 
{
    bool row = false;
    bool col = false;
    for (int i = 0; i < matrix.size(); i++)
    {
        for (int j = 0; j < matrix[0].size(); j++)
        {
            if (matrix[i][j] == 0)
            {
                matrix[i][0] = 0;
                matrix[0][j] = 0;
                if (i == 0)
                {
                    col = true;
                }
                if (j == 0)
                {
                    row = true;
                }
            }
        }
    }

    for (int i = 1; i < matrix.size(); i++)  //先变除去第0行第0列的，最后变第0行第0列
    {
        for (int j = 1; j < matrix[0].size(); j++)
        {
            if (matrix[i][0] == 0 || matrix[0][j] == 0)
            {
                matrix[i][j] = 0;
            }
        }
    }
    if (row)  //如果row被标记为true，第0列最后全变为0，下面同理
    {
        for (int i = 0; i < matrix.size(); i++)
        {
            matrix[i][0] = 0;
        }
    }
    if (col)
    {
        for (int i = 0; i < matrix[0].size(); i++)
        {
            matrix[0][i] = 0;
        }
    }
}

题目6(lc69)

给你一个非负整数 x ，计算并返回 x 的算术平方根。

由于返回类型是整数，结果只保留整数部分，小数部分将被舍去。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：
输入：x = 4
输出：2

示例 2：
输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

0 <= x <= 231 - 1

思路

二分法：
mid * mid > x 时证明太大了r = mid - 1，
mid * mid < x 时证明太小了或者就是正确答案，将ans暂时设置为mid，l = mid + 1，进下一次循环
mid * mid == x 时证明找到了正确答案，将ans设置为mid，然后直接break

代码

int mySqrt(int x) 
{
    long long l = 1;
    long long r = x;
    long long mid;    //不用long long当mid * mid时会溢出
    int ans = 0;
    while(l <= r)
    {
        mid = l + (r - l) / 2;
        if(mid * mid == x)
        {
            ans = mid;
            break;
        }
        else if(mid * mid > x)
        {
            r = mid - 1;
        }
        else
        {
            ans = mid;
            l = mid + 1;
        }
    }
    return ans;
}

题目7(lc36)

请你判断一个 9 x 9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 '.' 表示。

示例 1：

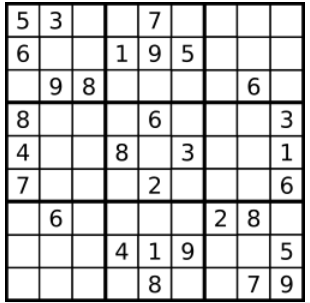
输入：board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

思路

准备三个bool类型矩阵，分别对应每一行的1~9出现与否、每一列的1~9出现与否、每一个3*3宫内的1~9出现与否，碰到对应数字就把对应位置置为true，每次置之前要判断是否是false，如果是已经被置为true，代表同样的数字出现两次，返回false。如果遍历完矩阵还没返回就返回true。
注意一点是3*3宫内与数独矩阵下标的对应。从左上角开始到右下角，是第0号宫 ~ 第8号宫，对应bool类型矩阵的0 ~ 8行。在数独矩阵中下标为i, j的位置对应bool类型矩阵中宫的编号为：3 * (i/3) + (j/3)。注意3 * (i/3)不能把3约去，因为(i/3)是整数除法。

代码

bool isValidSudoku(vector<vector<char>>& board) 
{
    vector<vector<bool>> row(9, vector<bool>(10));
    vector<vector<bool>> col(9, vector<bool>(10));
    vector<vector<bool>> bucket(9, vector<bool>(10));
    for (int i = 0; i < 9; i++)
    {
        for (int j = 0; j < 9; j++)
        {
            if (board[i][j] != '.')
            {
                int bid = 3 * (i / 3) + (j / 3);
                int num = board[i][j] - '0';
                if (row[i][num] || col[j][num] || bucket[bid][num])
                {
                    return false;
                }
                row[i][num] = true;
                col[j][num] = true;
                bucket[bid][num] = true;
            }
            
        }
    }
    return true;
}

题目8(lc37)

编写一个程序，通过填充空格来解决数独问题。

数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用 '.' 表示。

示例 1：

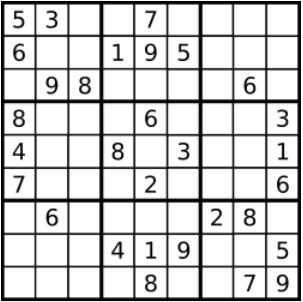
输入：board = [["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]]

输出：[["5","3","4","6","7","8","9","1","2"],
["6","7","2","1","9","5","3","4","8"],
["1","9","8","3","4","2","5","6","7"],
["8","5","9","7","6","1","4","2","3"],
["4","2","6","8","5","3","7","9","1"],
["7","1","3","9","2","4","8","5","6"],
["9","6","1","5","3","7","2","8","4"],
["2","8","7","4","1","9","6","3","5"],
["3","4","5","2","8","6","1","7","9"]]

解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

思路

先利用上一题的做法生成每一行的1~9出现与否、每一列的1~9出现与否、每一个3*3宫内的1~9出现与否的三个矩阵信息，然后带着这个信息回溯法递归求解。具体思路看代码

代码

//生成每一行的1 ~ 9出现与否、每一列的1 ~ 9出现与否、每一个3*3宫内的1 ~ 9出现与否的三个矩阵信息
void initInfos(vector<vector<char>>& board, vector<vector<bool>> &row, vector<vector<bool>> &col, vector<vector<bool>> &bucket)
{
    for (int i = 0; i < 9; i++)
    {
        for (int j = 0; j < 9; j++)
        {
            if (board[i][j] != '.')
            {
                int bid = 3 * (i / 3) + (j / 3);
                int num = board[i][j] - '0';
                row[i][num] = true;
                col[j][num] = true;
                bucket[bid][num] = true;
            }
            
        }
    }
}

//回溯法递归
bool process(vector<vector<char>>& board, int i, int j, vector<vector<bool>>& row, vector<vector<bool>>& col, vector<vector<bool>>& bucket)
{
    if (i == 9)  
    {
        //越界了，证明数独填完了，返回true
        return true;
    }

    //设置下一个位置的行列下标，递归是从左到右从上到下填，到了右边界就进下一行
    int nexti = j != 8 ? i : i + 1;    //设置下一个位置的行下标
    int nextj = j != 8 ? j + 1 : 0;    //设置下一个位置的列下标

    //当前位置是数字，调用下一个位置的递归
    if (board[i][j] != '.')
    {
        return process(board, nexti, nextj, row, col, bucket);
    }
    else
    {
        //当前位置是'.'
        int bid = 3 * (i / 3) + (j / 3);
        for (int num = 1; num <= 9; num++)  //从1 ~ 9开始尝试
        {
            if ((!row[i][num]) && (!col[j][num]) && (!bucket[bid][num]))  //必须行、列、宫都没出现过当前尝试的数字
            {
                //设置信息
                row[i][num] = true;
                col[j][num] = true;
                bucket[bid][num] = true;
                board[i][j] = num + '0';

                //如果成功了返回true
                if (process(board, nexti, nextj, row, col, bucket))
                {
                    return true;
                }

                //递归失败，把信息设置回去
                row[i][num] = false;
                col[j][num] = false;
                bucket[bid][num] = false;
                board[i][j] = '.';
            }
        }
        return false;
    }
}

void solveSudoku(vector<vector<char>>& board) //主函数
{
    vector<vector<bool>> row(9, vector<bool>(10));
    vector<vector<bool>> col(9, vector<bool>(10));
    vector<vector<bool>> bucket(9, vector<bool>(10));
    initInfos(board, row, col, bucket);
    process(board, 0, 0, row, col, bucket);
}

题目9(lc20)

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例 1：
输入：s = "()"
输出：true

示例 2：
输入：s = "()[]{}"
输出：true

示例 3：
输入：s = "(]"
输出：false

思路

准备一个栈，遇到左括号进栈，遇到右括号就弹出栈顶，并判断弹出的半个括号是否与当前右括号配对，如果不配对就返回false，如果配对就继续，直到出界并且栈为空返回true。

代码

bool isValid(string s) 
{
    stack<char> Stack;
    for (int i = 0; i < s.size(); i++)
    {
        if (s[i] == '(' || s[i] == '[' || s[i] == '{')
        {
            Stack.push(s[i]);
        }
        else
        {
            if (Stack.empty())
            {
                return false;
            }
            char tmp = Stack.top();
            Stack.pop();
            if ((tmp == '(' && s[i] == ')') || (tmp == '[' && s[i] == ']') || (tmp == '{' && s[i] == '}'))
            {
                continue;
            }
            else
            {
                return false;
            }
        }
    }
    return Stack.empty();
}

题目10

企鹅厂每年都会发文化衫，文化衫有很多种颜色，厂庆的时候，企鹅们都需要穿文化衫来拍照。一次采访中，记者随机遇到的企鹅，企鹅会告诉记者还有多少个企鹅跟他穿同样颜色的文化衫。记者可能不会收集所有企鹅的回答，但是每个企鹅的回答都是100%正确的。给定一个数组，里面是收集到的所有企鹅的回答，返回最少的企鹅数量。
示例 1：
输入：answers = [1]
输出：2
解释：一个人回答，还有1个人跟他穿一样颜色的文化衫，所以最少是2个人。

示例 2：
输入：answers = [1, 1, 2]
输出：5
解释：第一个人回答，还有1个人跟他穿一样颜色的文化衫，第二个人回答，还有1个人跟他穿一样颜色的文化衫，此时假设第1个人和第2个人穿同样颜色的文化是，那么当前就是最少2个人。第三个人回答还有2个人跟他穿一样颜色的文化衫，他不可能与第一个、第二个人穿同样颜色的文化衫，所以一定至少还有3个人穿与第一个人、第二个人不同颜色的文化衫。所以最少是5个人。

思路

先从小到大排序，

posted @ 2022-10-06 09:14 小肉包i 阅读(43) 评论(0) 收藏举报

刷新页面返回顶部