字节笔试算法题
题目1
给定一个字符串，进行以下操作：
- 三个同样的字母连在一起，去掉一个：比如 helllo -> hello
- 两对一样的字母（AABB型）连在一起，去掉第二对的一个字母：比如 helloo -> hello
- 上面的规则优先“从左到右”匹配，即如果是AABBCC，虽然AABB和BBCC都是错误拼写，应该优先考虑修复AABB，结果为AABCC
数据范围：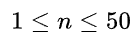
，每个用例的字符串长度满足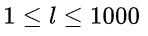 
输入描述:
第一行包括一个数字N，表示本次用例包括多少个待校验的字符串。
后面跟随N行，每行为一个待校验的字符串。
输出描述:
N行，每行包括一个被修复后的字符串。
思路
思路1：定义一个指针p，从前往后扫描一遍，满足第1和第2条规则时p不变，处理字符串，不满足条件的其他情况下p++，直到p处于倒数第二个字符(因为满足条件至少需要3个字符)，跳出循环
思路2：正则匹配
代码
#include <iostream>
#include <cstdio>
#include <vector>
#include <string>
using namespace std;
string check(string str)
{
if (str.size() < 3)
{
return str;
}
int p1 = 0;
while (p1 < str.size() - 1)
{
if (p1 + 2 < str.size() && str[p1] == str[p1 + 1] && str[p1] == str[p1 + 2])
{
str.erase(p1, 1);
}
else if (p1 + 3 < str.size() && str[p1] == str[p1 + 1] && str[p1 + 2] == str[p1 + 3])
{
str.erase(p1 + 2, 1);
}
else
{
p1++;
}
}
return str;
}
int main()
{
int N;
cin >> N;
string str;
for (int i = 0; i < N; i++)
{
cin >> str;
cout << check(str) << endl;
}
return 0;
}
相关函数介绍
string& erase(size_t pos=0, size_t len = npos);
//其中，参数pos表示要删除字符串的起始位置，其默认值是0；len表示要删除字符串的长度，其默认值是string::npos。返回值是删除后的字符串。
string &replace(size_t pos, size_t len, const &str)
//其中，参数pos表示要替换的字符串的起始位置；len表示要替换的字符串的长度。str是要替换成什么字符串，返回值是替换后的字符串。
错误总结
string tmp = "";
tmp = '1' + '2'; //tmp的结果不是"12"，而是char('1'+'2');
//将tmp变为"12"的正确做法
tmp += '1';
tmp += '2';
题目2
我叫王大锤，是一名特工。我刚刚接到任务：在字节跳动大街进行埋伏，抓捕恐怖分子孔连顺。和我一起行动的还有另外两名特工，我提议
- 我们在字节跳动大街的 N 个建筑中选定 3 个埋伏地点。
- 为了相互照应，我们决定相距最远的两名特工间的距离不超过 D 。
给定 N（可选作为埋伏点的建筑物数）、 D（相距最远的两名特工间的距离的最大值）以及可选建筑的坐标，计算在这次行动中，有多少种埋伏选择。
注意：
- 两个特工不能埋伏在同一地点
- 三个特工是等价的：即同样的位置组合( A , B , C ) 只算一种埋伏方法，不能因“特工之间互换位置”而重复使用
输入描述:
第一行包含空格分隔的两个数字 N和D(1 ≤ N ≤ 1000000; 1 ≤ D ≤ 1000000)
第二行包含N个建筑物的的位置，每个位置用一个整数（取值区间为[0, 1000000]）表示，从小到大排列（将字节跳动大街看做一条数轴）
输出描述:
一个数字，表示不同埋伏方案的数量。结果可能溢出，请对 99997867 取模
思路
我们只需要考虑相距最远的两个特工之间是否超过了D，如果没有超过，则三个特工可以埋伏的位置就是窗口内(包括左右两边)所有位置的排列组合。
接下来就是采用滑动窗口，窗口不回退模型。由于可能会涉及重复计算，所以下面采用的是固定首位计算，即窗口左边界必定作为第一个特工的埋伏地点，剩下两位特工在其他位置上选择。
流程：起始时窗口的两边都在0位置，然后窗口右边界开始往外扩，扩到最大时(窗口两边只差小于等于D)，开始统计方案数，统计完本次方案数后，窗口左边界向右移动一次，窗口有边界继续往右扩到最右，然后统计，窗口左边界继续向右移动一个位置...直到窗口左边界越界。这样做的好处是每次都固定首位，统计第一个特工在数组每一个位置时，另外两个特工可以选择的位置，这样不会重复。
代码
#include <iostream>
#include <cstdio>
#include <vector>
#include <string>
using namespace std;
int main()
{
long long N, D;
cin >> N >> D;
vector<long long> vec(N);
for (long long i = 0; i < N; i++)
{
cin >> vec[i];
}
if (N < 3 || D < 2)
{
cout << "0" << endl;
return 0;
}
int p1 = 0, p2 = 0;
long long ans = 0;
for (; p1 < N; p1++)
{
while (vec[p2] - vec[p1] <= D && p2 < N)
{
p2++;
}
long long x = p2 - p1 - 1; //因为while循环的特性，当跳出循环时，p2的位置是能扩得到的最远位置+1，所以这里统计一共有多少个位置时多-1 2
ans += x * (x - 1) / 2; //排列组合的计算公式C
X
ans %= 99997867;
}
cout << ans << endl;
return 0;
}
涉及知识
排列组合公式
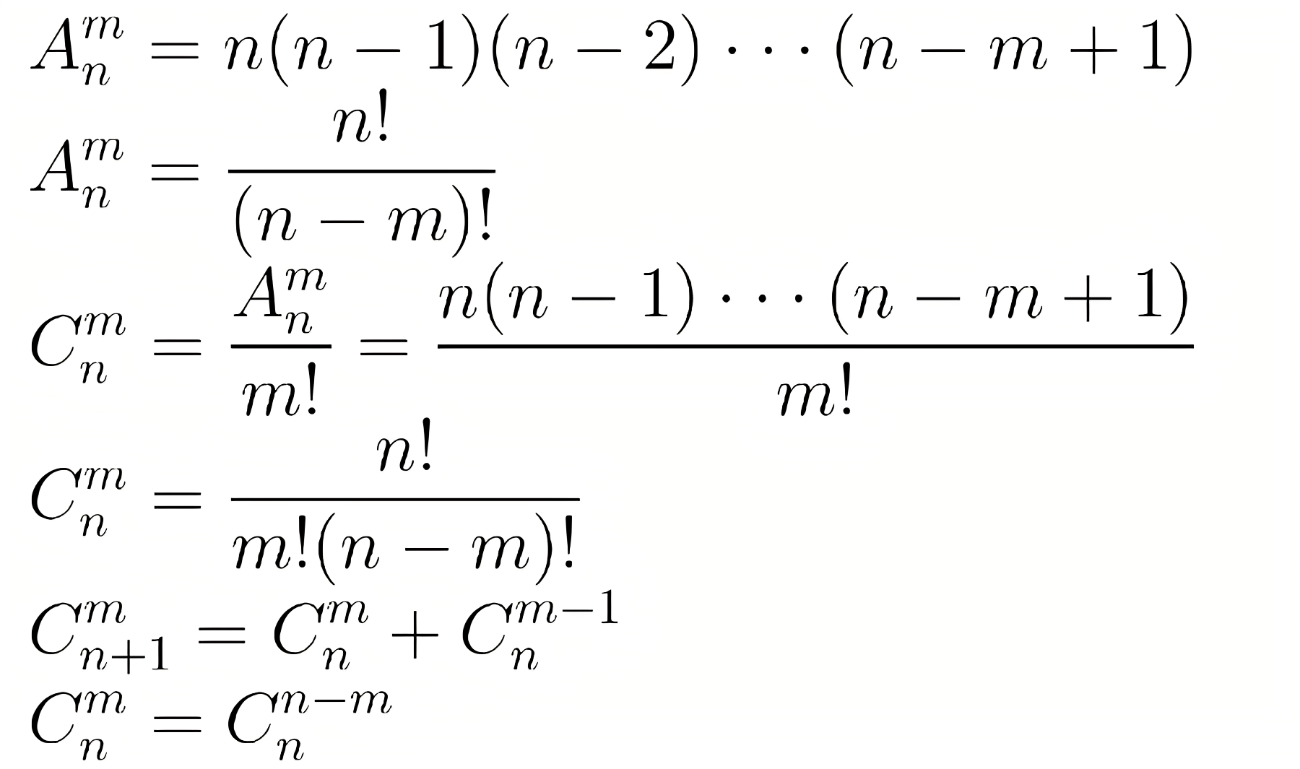
题目3
小包最近迷上了一款叫做雀魂的麻将游戏，但是这个游戏规则太复杂，小包玩了几个月了还是输多赢少。
于是生气的小包根据游戏简化了一下规则发明了一种新的麻将，只留下一种花色，并且去除了一些特殊和牌方式（例如七对子等），具体的规则如下：
总共有36张牌，每张牌是1~9。每个数字4张牌。
你手里有其中的14张牌，如果这14张牌满足如下条件，即算作和牌
14张牌中有2张相同数字的牌，称为雀头。
除去上述2张牌，剩下12张牌可以组成4个顺子或刻子。顺子的意思是递增的连续3个数字牌（例如234,567等），刻子的意思是相同数字的3个数字牌（例如111,777）
例如：
1 1 1 2 2 2 6 6 6 7 7 7 9 9 可以组成1,2,6,7的4个刻子和9的雀头，可以和牌
1 1 1 1 2 2 3 3 5 6 7 7 8 9 用1做雀头，组123,123,567,789的四个顺子，可以和牌
1 1 1 2 2 2 3 3 3 5 6 7 7 9 无论用1 2 3 7哪个做雀头，都无法组成和牌的条件。
现在，小包从36张牌中抽取了13张牌，他想知道在剩下的23张牌中，再取一张牌，取到哪几种数字牌可以和牌。
输入描述:
输入只有一行，包含13个数字，用空格分隔，每个数字在1~9之间，数据保证同种数字最多出现4次。
输出描述:
输出同样是一行，包含1个或以上的数字。代表他再取到哪些牌可以和牌。若满足条件的有多种牌，请按从小到大的顺序输出。若没有满足条件的牌，请输出一个数字0
思路
回溯法，因为牌只有1-9，所以利用回溯法列出所有可能性的递归次数不会太大。具体思路看下面代码的注释
代码
#include <iostream>
#include <vector>
#include <map>
using namespace std;
bool isHu(map<int, int> mp, int num) //递归函数，是否胡牌
{
if (num <= 0) //num小于或等于0代表能胡牌
{
return true;
}
while (mp[mp.begin()->first] == 0) //移除map中value为0的key
{
mp.erase(mp.begin()->first);
}
map<int, int>::iterator it = mp.begin(); //每次选择大小最小的牌，且数量不是0的牌作为当前要操作的牌
if (num % 3 != 0 && (it->second) >= 2) //num % 3 != 0 代表没有出现过雀头，因为其他使num减小的操作都是一次减小3个，只有雀头减小2个才会使num变成3的倍数。且只能选择一次雀头，因为一旦选择了雀头，那么num永远都是3的倍数，就不会进入这个if内。
{ //当没有出现过雀头，且当前牌的数量大于等于2，则选择当前的牌做雀头
mp[it->first] -= 2; //当前的牌选做雀头，数量减少2
if (isHu(mp, num - 2)) //调用递归判断当前的牌选做雀头时是否可以胡牌
{
return true;
}
mp[it->first] += 2; //递归调用失败，选做雀头不能胡牌，恢复当前牌的数量
}
if ((it->second) >= 3) //已经出现过雀头了，当前牌的数量大于3，则可以选择刻子
{
mp[it->first] -= 3; //选为刻子，数量-3
if (isHu(mp, num - 3))
{
return true;
}
mp[it->first] += 3; //递归调用失败，选做刻子不能胡牌，恢复当前牌的数量
}
if ((it->second) > 0 && mp[(it->first) + 1] > 0 && mp[(it->first) + 2] > 0) //当前牌不能选做雀头和刻子，那么就判断是否能选做顺子
{
mp[it->first]--;
mp[(it->first) + 1]--;
mp[(it->first) + 2]--;
if (isHu(mp, num - 3))
{
return true;
}
mp[it->first]++; //递归调用失败，选做顺子不能胡牌，恢复当前牌的数量
mp[(it->first) + 1]++;
mp[(it->first) + 2]++;
}
return false;
}
int main()
{
map<int, int> mp;
int tmp;
for (int i = 0; i < 13; i++) //统计牌的数量
{
cin >> tmp;
mp[tmp]++;
}
int flag = false; //判断是否无论如何都不能胡牌
for (int i = 1; i < 10; i++) //因为牌只有1-9，所以循环9次，判断这9个哪个牌当成被额外选择的牌时可以胡牌
{
if (mp[i] < 4) //当前牌的数量小于3，可以选择当前牌为额外选择的牌
{
mp[i]++; //选择当前牌为额外选择的牌，数量+1
if (isHu(mp, 14))
{
flag = true; //flag置为true，代表胡牌了
cout << i << " ";
}
mp[i]--; //不能胡牌，恢复原来的数量
}
}
if (!flag) //没有胡牌，输出0
{
cout << 0 << endl;
}
return 0;
}
涉及知识
回溯法
引申到DFS
题目4
小明是一名算法工程师，同时也是一名铲屎官。某天，他突发奇想，想从猫咪的视频里挖掘一些猫咪的运动信息。为了提取运动信息，他需要从视频的每一帧提取“猫咪特征”。一个猫咪特征是一个两维的vector<x, y>。如果x_1=x_2 and y_1=y_2，那么这俩是同一个特征。
因此，如果喵咪特征连续一致，可以认为喵咪在运动。也就是说，如果特征<a, b>在持续帧里出现，那么它将构成特征运动。比如，特征<a, b>在第2/3/4/7/8帧出现，那么该特征将形成两个特征运动2-3-4 和7-8。
现在，给定每一帧的特征，特征的数量可能不一样。小明期望能找到最长的特征运动。
输入描述:
第一行包含一个正整数N，代表测试用例的个数。
每个测试用例的第一行包含一个正整数M，代表视频的帧数。
接下来的M行，每行代表一帧。其中，第一个数字是该帧的特征个数，接下来的数字是在特征的取值；比如样例输入第三行里，2代表该帧有两个猫咪特征，<1，1>和<2，2>
所有用例的输入特征总数和<100000
N满足1≤N≤100000，M满足1≤M≤10000，一帧的特征个数满足 ≤ 10000。
特征取值均为非负整数。
输出描述:
对每一个测试用例，输出特征运动的长度作为一行
输入例子1:
1
8
2 1 1 2 2
2 1 1 1 4
2 1 1 2 2
2 2 2 1 4
0
0
1 1 1
1 1 1
输出例子1:
3
例子说明1:
特征<1,1>在连续的帧中连续出现3次，相比其他特征连续出现的次数大，所以输出3
思路
建立两张map，第一张map1的key储存出现过的特征，value储存其连续出现的次数；第二张map2的key储存出现过的特征，value储存其上一次是在第几帧出现的。定义一个变量max，初始值为0，代表截至目前为止出现过的最长的特征运动的次数(最长的连续出现的特征的次数)。随着输入，更新两张map，如果当前帧的当前特征在之前没有出现过，或者出现过但是上一次出现的帧数不是上一帧，则更新当前特征在map1的value为1，map2的value为当前帧；如果当前帧的当前特征在之前出现过且上一次出现的帧数是上一帧，则更新当前特征在map1的value++，map2的value为当前帧。更新完当前特征的map1和map2之后，将其map1的value与max比较，更新max的值。直到当前用例所有帧数更新完毕，输出max，进下一次用例循环。
代码
#include <iostream>
#include <cstdio>
#include <vector>
#include <string>
#include <map>
using namespace std;
int main()
{
int N;
cin >> N;
while (N--)
{
int M;
cin >> M;
int num;
int max = 0;
map<string, int> m1;
map<string, int> m2;
for (int i = 0; i < M; i++)
{
cin >> num;
for (int j = 0; j < num; j++)
{
string x;
string y;
cin >> x;
cin >> y;
string str = x + "#" + y;
if (m1.count(str) == 0 || m2[str] != i - 1)
{
m1[str] = 1;
}
else
{
m1[str]++;
}
m2[str] = i;
max = max > m1[str] ? max : m1[str];
}
}
cout << max << endl;
}
return 0;
}
涉及知识
map的运用
题目5
Z国的货币系统包含面值1元、4元、16元、64元共计4种硬币，以及面值1024元的纸币。现在小Y使用1024元的纸币购买了一件价值为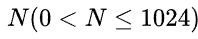
的商品，请问最少他会收到多少硬币？
输入描述:
一行，包含一个数N。
输出描述:
一行，包含一个数，表示最少收到的硬币数。
思路
01背包问题，动态规划
代码
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> money = { 1,4,16,64 };
vector<int> dp(1024 - n + 1); //dp[i]的含义：能拼成i元钱所需要的最少的硬币数量
for (int i = 0; i < dp.size(); i++) //赋初值，最大值，都用1元硬币拼
{
dp[i] = i;
}
for (int i = 1; i <= 1024 - n; i++)
{
for (int j = 0; j < money.size(); j++)
{
if (i >= money[j]) //当要拼成的钱数大于等于当前硬币的面值，代表当前硬币可以用，找到左边离它最近的dp值，与自己比较，取最小值
{
dp[i] = min(dp[i - money[j]] + 1, dp[i]);
}
}
}
cout << dp[1024 - n] << endl;
return 0;
}
题目6
机器人正在玩一个古老的基于DOS的游戏。游戏中有N+1座建筑——从0到N编号，从左到右排列。编号为0的建筑高度为0个单位，编号为i的建筑的高度为H(i)个单位。
起初， 机器人在编号为0的建筑处。每一步，它跳到下一个（右边）建筑。假设机器人在第k个建筑，且它现在的能量值是E, 下一步它将跳到第个k+1建筑。它将会得到或者失去正比于与H(k+1)与E之差的能量。如果 H(k+1) > E 那么机器人就失去 H(k+1) - E 的能量值，否则它将得到 E - H(k+1) 的能量值。
游戏目标是到达第个N建筑，在这个过程中，能量值不能为负数个单位。现在的问题是机器人以多少能量值开始游戏，才可以保证成功完成游戏？
输入描述:
第一行输入，表示一共有 N 组数据.
第二个是 N 个空格分隔的整数，H1, H2, H3, ..., Hn 代表建筑物的高度
输出描述:
输出一个单独的数表示完成游戏所需的最少单位的初始能量
思路
当 H(k+1) > E 时，变化完的能力为 E' = E - (H(k+1) - E) = 2E - H(k+1);
当 H(k+1) <= E 时，变化完的能力为 E' = E + E - H(k+1)= 2E - H(k+1);
两者相等，即每次跳跃之后都会变成2E - H(k+1)的能量。假设到最后一栋楼时的能力为0，从后往前推，即可求得最开始的最小值。
假设当前能量为x，处于H(K)，则处于H(K-1)时的能量x' = (x + h(k)) / 2，但是注意程序里是int类型，所以除以2时需要向上取整 x' = (x + h(k) + 1) / 2
代码
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> vec(n);
for(int i = 0; i < n; i++)
{
cin >> vec[i];
}
int e = 0;
for(int i = n - 1; i >= 0; i--)
{
e = (e + vec[i] + 1) / 2; //注意括号里多+1是为了除以2以后向上取整，否则当遇上除以2出现0.5的情况e会比实际小
}
cout << e << endl;
return 0;
}
题目7
思路
动态规划，注意status的含义
代码
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int getNum(vector<vector<int>> &ma)
{
const int MAX = 0x0fffffff;
int n = ma.size();
int status = 1 << n; //status含义：二进制位从低位到高位分别代表每个城市的状态，0代表没去过，1代表去过
vector<vector<int>> dp(status, vector<int>(n, MAX)); //定义dp数组，并给每个位置赋初值MAX。dp的含义：i中去过的城市，以j结尾，花费的最少的钱
dp[1][0] = 0; //从0出发，所以0一定去过了，从0到0花费的钱为0
for (int i = 1; i < status; i++)
{
for (int j = 0; j < n; j++)
{
if (dp[i][j] != MAX)
{ //如果达到过j(去过哪个地方是由下面的循环更新的)
for (int k = 0; k < n; k++)
{
if ((i & (1 << k)) == 0)
{ //没去过k，更新k。dp[i | (1 << k)][k]：去过k，以k结尾，当前花费的最少的钱。dp[i][j] + ma[j][k]：从j到k花费的钱
dp[i | (1 << k)][k] = min(dp[i | (1 << k)][k], dp[i][j] + ma[j][k]);
}
}
}
}
}
int res = MAX;
for (int i = 1; i < n; i++)
{
res = min(dp[status - 1][i] + ma[i][0], res);
}
return res;
}
int main()
{
int n;
while(cin>>n){
vector<vector<int>> edges(n,vector<int>(n,0));
int x;
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
cin>>edges[i][j];
}
}
cout<<getNum(edges)<<endl;
}
return 0;
}
浙公网安备 33010602011771号