算法进阶（1）：排序后相邻两数最大差值、最多不重叠非空子区间异或和等于0、背包问题变种(两种背包问题拼起来)
题目1
给定一个数组，求如果排序之后，相邻两数的最大差值。要求时间复杂度0(N)，且要求不能用非基于比较的排序。
思路
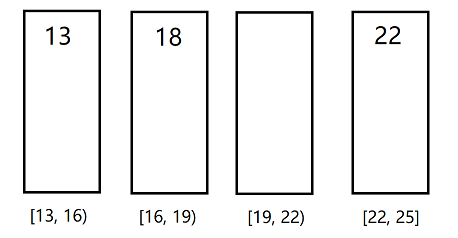
假设数组的长度是N，遍历一遍数组，找到整个数组的最大值和最小值，按照最大值和最小值的差值，将数组大小范围平分成N+1个桶(桶就是容器，可以是队列)，值属于桶内就把这个数放进桶里，但是保证桶里顺序是从小到大。将桶按照编号从小到大依次倒出的顺序就是最后排序的顺序。因为桶的个数是N+1个，所以必定会有至少一个桶是空的，当前非空桶的最后一个数与下一个非空桶第一个数一定是排完序相邻的数，同一个桶中的相邻数字在排完序后位置也是一样的。由于单个桶存储数字的范围是按照最大值和最小值的差值均分的，最小值一定在第一个桶里，最大值一定在最后一个桶里，所以空桶一定是在中间。因为相邻两个桶之间的差值是固定的，假设第i个桶是空桶，i-1和i+1不是空桶，那么i+1中的第一个数字与i-1中的最后一个数字(排完序相邻)的差值一定比任何一个桶中两个相邻数字的差值大，但是假设i-2也是非空桶，中间隔着空桶的差值不一定会比相邻桶的差值大。如下图，22 - 18 = 4，18 - 13 = 5。所以我们只需要统计所有非空桶最后一个数与下一个非空桶第一个数的差值，找出它们之间最大的即可。注意，本题虽然用到了桶，但是实质依然是基于比较的排序。
方法总结
寻找平凡解排除一部分错误答案。我们为什么要分N+1个桶而不是N个桶，就是为了保证一定会有至少一个空桶，多了这一个空桶，我们就找到了一种平凡解，即中间有空桶的两个非空桶，后面桶的第一个值减去前面桶的最后一个值的差值就是平凡解。它不一定是最优解，有可能成为最优解，但绝对不是最差解。通过这个平凡解就可以把单个桶内部相邻数的差值忽略，即排除比它更差的解，这样我们可以把结果只聚焦在所有非空桶最后一个数与下一个非空桶第一个数的差值上，忽略了单个桶内部的比较，这是个时间复杂度为O(N)的过程。通过这种方式降低算法整体的时间复杂度。
代码
int getID(long max, long min, long size, long i);
int maxDiff(vector<int> arr)
{
if (arr.size() < 2)
{
return 0;
}
int max = INT_MIN;
int min = INT_MAX;
for (int i = 0; i < arr.size(); i++)
{
max = max > arr[i] ? max : arr[i];
min = min < arr[i] ? min : arr[i];
}
if (max == min)
{
return 0;
}
vector<int> maxs(arr.size() + 1);
vector<int> mins(arr.size() + 1); //因为计算过程中只需要三个信息，桶中的最大值、最小值，桶是不是空的
vector<bool> notEmpty(arr.size() + 1); //所以用三个数组代表桶，分别储存这三个信息
int bID = 0; //桶编号
for (int i = 0; i < arr.size(); i++)
{
bID = getID(max, min, arr.size(), arr[i]);
maxs[bID] = notEmpty[bID] ? (maxs[bID] > arr[i] ? maxs[bID] : arr[i]) : arr[i];
mins[bID] = notEmpty[bID] ? (mins[bID] < arr[i] ? mins[bID] : arr[i]) : arr[i];
notEmpty[bID] = true; //把默认的false置为true，只有false变true，没有true变false
}
int ans = 0;
int lastNum = maxs[0];
for (int i = 1; i < maxs.size(); i++)
{
if (notEmpty[i])
{
ans = ans > (lastNum - mins[i]) ? ans : lastNum - mins[i];
lastNum = maxs[i];
}
}
return ans;
}
int getID(long max, long min, long size, long i) //最简洁的写法，比较难想，可以采用简单的写法
{
return (int)(i - min) * size / (max - min);
}
题目2
给出n个数字a_1.....a_n， 问最多有多少不重叠的非空区间，使得每个区间内数字的xor(异或和)都等于0。
思路
本题采用动态规划的方法，dp[i]的值代表从0~i位置最优划分下异或和为0的区间数(最优划分即异或和为0的不重叠非空区间最多)，dp[0]，的值取决于数组0位置的值是否是0，如果是dp[0] = 1，否则dp[0] = 0。
那么如何求解dp[i]的值？可能性讨论。首先，i位置一定是0~i之间最优划分下的最后一部分的最后一个数(不管这最后一部分异或和是否为0)，所以有两种可能性。第一种是最优划分下i位置所属的这最后一部分异或和不为0，那么dp[i]的值就等于dp[i-1]。第二种是最优划分下i位置所属的这最后一部分异或和为0。
接下来我们利用假设答案法，假设0~i范围下最优划分如右图所示，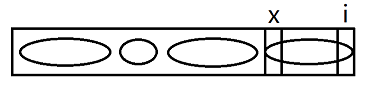
，最后一部分划分异或和为0，x为开头位置，i为结尾位置。那么x位置一定是离i最近的使得从自己开始异或和到i为0的位置。利用反证法，假设还有一个比x离i更近的y，从y开始异或和到i为0，那么x到i异或和为0，y到i异或和为0，则x到y异或和也一定为0，这种情况下从y处劈开，y到i才是最后一部分划分，x到y是倒数第二部分划分，这与我们之前假设的最优划分矛盾了，所以x一定是离i最近的使得从自己开始异或和到i为0的位置。
有了上面的结论，我们就可以知道，第二种可能性的情况下，x到i是最后一部分划分，那么dp[i] = max{dp[i-1]，dp[x-1] + 1}。问题就是如何求得x的位置？假设0~i位置的异或和是e，那么上一次出现 0到某一个位置的异或和是e的 这个某一个位置就是x-1位置，注意这个上一次必须是最近一次。准备一个变量eor，初始值为0。准备一个哈希表map，key存放eor的值，value存放位置信息。每到达一个位置就把这个位置上的值异或到eor上去，然后在哈希表中查找当前eor的值有没有出现过，如果有，则是第二种可能性，dp[i] = max{dp[i-1]，dp[map.at(eor)] + 1}，并更新map中当前eor出现的最后位置。如果没出现，则在map中添加这条记录，继续往后遍历数组。最后返回dp数组的最后一个值即可。
方法总结
本题目用到的是动态规划和假设答案法。假设答案法就是假设一个最优解的状况，然后看它有什么性质
代码
int eor(vector<int> arr)
{
if (arr.size() == 0)
{
return 0;
}
vector<int> dp(arr.size());
unordered_map<int, int> indexMap;
int eor = 0;
indexMap.insert(make_pair(0, -1));
for (int i = 0; i < arr.size(); i++)
{
eor ^= arr[i];
if (indexMap.count(eor) != 0)
{
dp[i] = indexMap.at(eor) == -1 ? 1 : dp[indexMap.at(eor) + 1]; //如果找到的位置是-1，代表从eor=0，且是第一次出现
indexMap.at(eor) = i;
}
else
{
indexMap.insert(make_pair(eor, i));
}
dp[i] = max(dp[i], dp[i - 1]); //当前异或和如果没有出现过，则相当于0与dp[i-1]比较，其实还是赋值为dp[i-1]
}
return dp[arr.size() - 1];
}
题目3
现有n1+n2种面值的硬币，其中前n1种为普通币，可以取任意枚，后n2种为纪念币，每种最多只能取一枚，每种硬币有一个面值，问能用多少种方法拼出m的面值?
思路
两个dp数组拼起来。n1拼0面值，n2拼m面值，两种方法数相乘；n1拼1面值，n2拼m-1面值，两种方法数相乘；n1拼2面值，n2拼m-1面值，两种方法数相乘；......；n1拼m面值，n2拼0面值，两种方法数相乘。最后所有的方法数加起来。两个dp数组都是经典的背包问题，表填完之后再for循环从0到m分别从dp1和dp2拿值相乘再累加即可。注意n1的表可以斜率优化。
int nums(vector<int> n1, vector<int> n2, int m)
{
if (n1.size() == 0 || n2.size() == 0 || m < 0)
{
return 0;
}
vector<vector<int>> dp1(n1.size(), vector<int>(m + 1));
vector<vector<int>> dp2(n2.size(), vector<int>(m + 1));
for (int i = 0; i < dp1.size(); i++)
{
dp1[i][0] = 1;
}
for (int i = 0; i < dp1[0].size(); i++)
{
if (i % n1[0] == 0)
{
dp1[0][i] == 1;
}
}
for (int i = 1; i < dp1.size(); i++)
{
for (int j = 1; j < dp1[0].size(); j++)
{
dp1[i][j] += dp1[i - 1][j];
dp1[i][j] += j - n1[i] >= 0 ? dp1[i - 1][j - n1[i]] : 0;
}
}
for (int i = 0; i < dp2.size(); i++)
{
dp2[i][0] = 1;
}
for (int i = 0; i < dp2[0].size(); i++)
{
if (i == n1[0])
{
dp2[0][i] == 1;
}
}
for (int i = 1; i < dp2.size(); i++)
{
for (int j = 1; j < dp2[0].size(); j++)
{
dp2[i][j] += dp2[i - 1][j];
dp2[i][j] += j - n2[i] >= 0 ? dp2[i - 1][j - n2[i]] : 0;
}
}
int ans = 0;
for (int i = 0; i <= m; i++)
{
ans += dp1[dp1.size() - 1][i] * dp2[dp2.size() - 1][m - i];
}
return ans;
}
浙公网安备 33010602011771号