算法提升(9):所有未出现的整数、人气值变化(递归陷入死循环的两种解决方法)、有限时间参加活动拿奖金(图的宽度优先遍历、有序表、贪心)、逻辑符号的组合方式、最长无重复子串、编辑距离问题、子序列字典序编号
题目1
给定一个整数数组A,长度为n,有1 <= A[i] <= n,且对于[1,n]的整数,其中部分整数会重复出现而部分不会出现。实现算法找到[1,n]中所有未出现在A中的整数。
提示:尝试实现0(n)的时间复杂度和0(1)的空间复杂度(返回值不计入空间复杂度)
输入描述:
一行数字,全部为整数,空格分隔
AO A1 A2 A3...
输出描述:
一行数字,全部为整数,空格分隔RO R1 R2 R3...
示例1:
输入
1 3 4 3
输出
2
思路
如果都出现过,则i对应的数为i+1。争取每个位置上放的都是对应值,当在i时,把它当前的数移动到它应该在的地方。目标位置的数如果跟它一样,则两个位置上的数都不变。如果不一样,把目标位置上的数拿出来,把它对应的数放上去,再对这个拿出来的数进行前面的操作把它放回自己对应的位置。最后再遍历一遍数组找出与位置不对应的数即可。
void modify(vector<int>& arr, int value);
void printNumNotInArr(vector<int>& arr)
{
if (arr.size() == 0)
{
return;
}
for (int i = 0; i < arr.size(); i++)
{
modify(arr, arr[i]);
}
for (int i = 0; i < arr.size(); i++)
{
if (arr[i] != i + 1)
{
cout << i + 1 << " ";
}
}
}
void modify(vector<int>& arr, int value)
{
while (arr[value - 1] != value)
{
int temp = arr[value - 1];
arr[value - 1] = value;
value = temp;
}
}
题目2
最近某直播平台在举行中秋之星主播唱歌比赛,假设一开始某主播的初始人气值为start,能够晋升下一轮人气需要刚好达到end,给主播增加人气的可以采取的方法有:
- 点赞花费x 币,人气 + 2
- 送礼花费y 币,人气 * 2
- 私聊花费z 币,人气 - 2
其中end远大于start且end为偶数,请写一个程序最少花费多少币就能帮助该主播将人气刚好达到end,从而能够晋级下一轮?
输入描述:
第一行输入5个数据,分别为: x,y,z,start,end
其中:0 < x,y,z <= 10000,0 < start ≪ end <= 1000000
输出描述:
需要花费的最少币。
示例1:
输入
3,100,1,2,6
输出
6
思路
首先我们采用暴力递归的思路,每次选择点赞、送礼或私聊,人气值变化,累加币,然后进入下一次递归,直到人气值达到end。但是会出现一个问题,这个递归会陷入死循环,比如起始人气值是2,目标是6,点赞后变成4,私聊后又变成了2,因为是暴力递归,每种方式都会罗列,所以永远跑不完。这时有两种解决方案:1. 找平凡解。就是一定能达到目标的决策方法所花费的代价。2. 从题目中找限制。本题的平凡解就是:因为start和end都是偶数,start一直加2加到end所花费的币coins就是一个平凡解,当花费的币大于coins时,就应该停止递归,因为你当前抉择的方式已经要比平凡解还要差了,那么你必然不可能是最优解。题目中的限制则是当前的人气值不能超过目标人气值的两倍,因为人气值减少的方式只有每次减少2,如果超过了目标值的两倍再往下减,那么代价比不扩大两倍往下减要大。有这两个限制条件,那么递归就能跑的完。
//暴力递归代码,虽然有了限制但是实际跑起来有的用例还是需要很长时间,不推荐。
int process(int x, int y, int z, int coins, int cur, int end, int limitAim, int limitCoins);
int minCoin(int x, int y, int z, int start, int end)
{
int limitCoins = (end - start) / 2 * x; //平凡解
int limitAim = end * 2; //题干中找到的限制
return process(x, y, z, 0, start, end, limitAim, limitCoins);
}
int process(int x, int y, int z, int coins, int cur, int end, int limitAim, int limitCoins)
{
if (cur < 0)
{
return INT_MAX;
}
if (cur > limitAim)
{
return INT_MAX;
}
if (coins > limitCoins)
{
return INT_MAX;
}
if (cur == end)
{
return coins;
}
int minCoins = INT_MAX;
int p1 = process(x, y, z, coins + x, cur + 2, end, limitAim, limitCoins);
minCoins = p1;
int p2 = process(x, y, z, coins + y, cur * 2, end, limitAim, limitCoins);
minCoins = min(minCoins, p2);
int p3 = process(x, y, z, coins + z, cur - 2, end, limitAim, limitCoins);
minCoins = min(minCoins, p3);
return minCoins;
}
//动态规划代码,没有递归,实际跑起来很快,推荐
int minCoins2(int x, int y, int z, int start, int end)
{
int limitCoins = (end - start) / 2 * x;
int limitAim = end * 2;
vector<vector<int>> dp(limitCoins + 1, vector<int>(limitAim + 1));
for (int i = 0; i <= limitCoins; i++)
{
dp[i][end] = i;
}
for (int i = limitCoins; i >= 0; i--)
{
for (int j = 0; j <= limitAim; j++)
{
if (j == end)
{
continue;
}
dp[i][j] = INT_MAX;
if (i + x <= limitCoins && j + 2 <= limitAim)
{
dp[i][j] = min(dp[i][j], dp[i + x][j + 2]);
}
if (i + z <= limitCoins && j - 2 >= 0)
{
dp[i][j] = min(dp[i][j], dp[i + z][j - 2]);
}
if (i + y <= limitCoins && j * 2 <= limitAim)
{
dp[i][j] = min(dp[i][j], dp[i + y][j * 2]);
}
}
}
return dp[0][start];
}
题目3
CC直播的运营部门组织了很多运营活动,每个活动需要花费一定的时间参与,主播每参加完一个活动即可得到一定的奖励,参与活动可以从任意活动开始,但一旦开始,就需要将后续活动参加完毕(注意:最后一个活动必须参与),活动之间存在一定的依赖关系(不存在环的情况),现在给出所有的活动时间与依赖关系,以及给出有限的时间,请帮主播计算在有限的时间内,能获得的最大奖励,以及需要的最少时长。
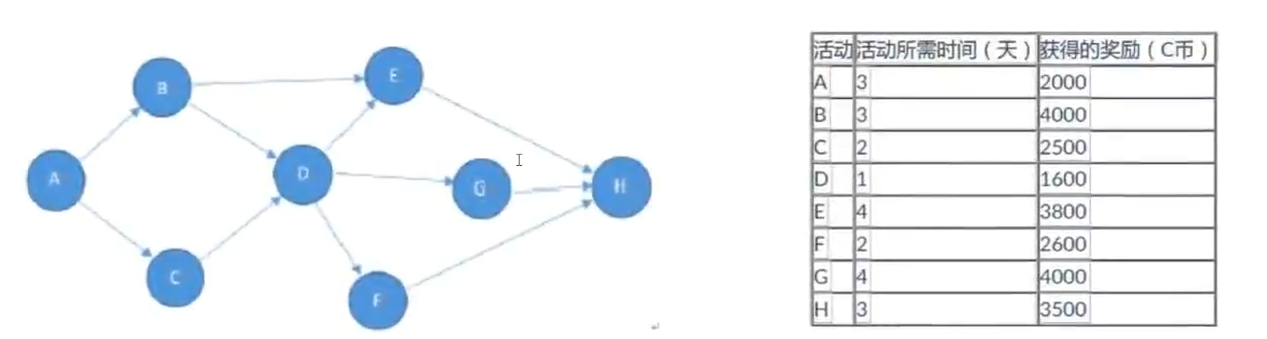
如上图数据所示,给定有限时间为10天。可以获取得最大奖励为:11700,需要的时长为:9天。参加的活动为BDFH四个。
输入描述:
第一行输入数据N与D,表示有N项活动,D表示给予的时长。0 < N <= 1000,0 < D <= 10000
从第二行开始到N+1行,每行描述一个活动的信息,其中第一项表示当前活动需要花费的时间t,第二项表示可以获得的奖励a,之后有N项数据,表示当前活动与其他活动的依赖关系,1表示有依赖,0表示无依赖。每项数据用空格分开。
输出描述:
输出两项数据A与T,用空格分割。A表示所获得的最大奖励,T表示所需要的时长。
输入
8 10
3 2000 0 1 1 0 0 0 0 0
3 4000 0 0 0 1 1 0 0 0
2 2500 0 0 0 1 0 0 0 0
1 1600 0 0 0 0 1 1 1 0
4 3800 0 0 0 0 0 0 0 1
2 2600 0 0 0 0 0 0 0 1
4 4000 0 0 0 0 0 0 0 1
3 3500 0 0 0 0 0 0 0 0
输出
11700 9
思路
因为是可以从任意活动开始,最后一个活动必须做,所以从后往前宽度优先遍历,每个节点都有一个有序表,key是已经花费的时间,value是已经赚取的钱数。每经过一个点把它后面连接的所有点的已经花费的时间和赚取的钱数的map的记录都加到自己上面来(加上自己的天数和钱),这就代表我到达当前活动的时候不同路线已经花费的天数和赚取的钱数,因为不止一条记录保证每条记录天数增加的同时钱数也增加,不符合要求的记录就删掉(因为天数多钱反而更少的活动路线没必要去),最后遍历到最开始的节点。把所有节点的有序表汇总成一个大表(为什么要汇总所有的记录,因为题干要求可以从任意活动开始,一直到最后一个活动),同样保证每条记录天数增加的同时钱数也增加,看输入的数据中给的天数,选在这个天数内钱数最多的记录。
题目4
给定一个只由0(假)、1(真)、&(逻辑与)、| (逻辑或)和^ (异或)五种字符组成的字符串express,再给定一个布尔值desired。返回express能有多少种组合方式,可以达到desired的结果。
[举例]
express="1^0|0|1",desired=false
只有1^((0|0)|1)和 1^(0|(0|1))的组合可以得到false, 返回2。
express="1",desired=false
无组合则可以得到false,返回0
思路
范围尝试模型,把每一个运算符都尝试作为最后一个结合的运算符。当来到i位置时(i为偶数,即运算符所在的位置),根据i位置运算符的情况,枚举左右两边L...i-1到i+1...R的合格运算结果的组合方式。然后再把左右两边继续递归重复
//递归代码
bool isValid(string express);
int process(int L, int R, string exp, bool desired);
int num1(string express, bool desired)
{
if (express.size() == 0)
{
return 0;
}
if (!isValid(express)) //判断传入的express是否合格,即是否是奇数个字符,奇数位上都是0或1,偶数位上都是运算符
{
return 0;
}
return process(0, express.size() - 1, express, desired);
}
int process(int L, int R, string exp, bool desired)
{
if (L == R) //当L==R时,就只剩一个数字,根据desired判断是否合格
{
if (exp[L] == '1')
{
return desired ? 1 : 0;
}
else
{
return desired ? 0 : 1;
}
}
int res = 0;
for (int i = L + 1; i < R; i += 2) //分别枚举每个运算符都是最后结合的情况
{
switch (exp[i])
{
case '&': {
if (desired)
{
res += process(L, i - 1, exp, true) * process(i + 1, R, exp, true);
break;
}
else
{
res += process(L, i - 1, exp, false) * process(i + 1, R, exp, true);
res += process(L, i - 1, exp, true) * process(i + 1, R, exp, false);
res += process(L, i - 1, exp, false) * process(i + 1, R, exp, false);
break;
}
}
case '|': {
if (desired)
{
res += process(L, i - 1, exp, true) * process(i + 1, R, exp, false);
res += process(L, i - 1, exp, false) * process(i + 1, R, exp, true);
res += process(L, i - 1, exp, true) * process(i + 1, R, exp, true);
break;
}
else
{
res += process(L, i - 1, exp, false) * process(i + 1, R, exp, false);
break;
}
}
case '^': {
if (desired)
{
res += process(L, i - 1, exp, true) * process(i + 1, R, exp, false);
res += process(L, i - 1, exp, false) * process(i + 1, R, exp, true);
break;
}
else
{
res += process(L, i - 1, exp, true) * process(i + 1, R, exp, true);
res += process(L, i - 1, exp, false) * process(i + 1, R, exp, false);
break;
}
}
default:
break;
}
}
return res;
}
bool isValid(string express)
{
if (express.size() % 2 != 1)
{
return false;
}
for (int i = 0; i < express.size(); i = i + 2)
{
if (express[i] != '0' && express[i] != '1')
{
return false;
}
}
for (int i = 1; i < express.size(); i = i + 2)
{
if (express[i] != '&' && express[i] != '|' && express[i] != '^')
{
return false;
}
}
return true;
}
//动态规划代码
int num2(string express, bool desired)
{
if (express.size() == 0)
{
return 0;
}
if (!isValid(express))
{
return 0;
}
int N = express.size();
vector<vector<int>> dpF(N, vector<int>(N));
vector<vector<int>> dpT(N, vector<int>(N));
for (int i = 0; i < N; i += 2)
{
dpF[i][i] = express[i] == '1' ? 0 : 1;
dpT[i][i] = express[i] == '1' ? 1 : 0;
}
for (int i = N - 3; i >= 0; i -= 2)
{
for (int j = i + 2; j < N; j += 2)
{
for (int k = i + 1; k < j; k += 2)
{
switch (express[k])
{
case '&': {
dpT[i][j] += dpT[i][k - 1] * dpT[k + 1][j];
dpF[i][j] += dpF[i][k - 1] * dpT[k + 1][j];
dpF[i][j] += dpT[i][k - 1] * dpF[k + 1][j];
dpF[i][j] += dpF[i][k - 1] * dpF[k + 1][j];
break;
}
case '|': {
dpT[i][j] += dpT[i][k - 1] * dpF[k + 1][j];
dpT[i][j] += dpF[i][k - 1] * dpT[k + 1][j];
dpT[i][j] += dpT[i][k - 1] * dpT[k + 1][j];
dpF[i][j] += dpF[i][k - 1] * dpF[k + 1][j];
break;
}
case '^': {
dpT[i][j] += dpT[i][k - 1] * dpF[k + 1][j];
dpT[i][j] += dpF[i][k - 1] * dpT[k + 1][j];
dpF[i][j] += dpF[i][k - 1] * dpF[k + 1][j];
dpF[i][j] += dpT[i][k - 1] * dpT[k + 1][j];
}
default:
break;
}
}
}
}
return desired ? dpT[0][N - 1] : dpF[0][N - 1];
}
题目5
在一个字符串中找到没有重复字符子串中最长的长度。
例如:
abcabcbb没有重复字符的最长子串是abc,长度为3
bbbbb,答案是b,长度为1
pwwkew,答案是wke,长度是3
要求:答案必须是子串,"pwke" 是一个子字符序列但不是一个子字符串。
思路
看到子数组、子字符串问题就想以每个位置作为结尾是什么情况。遍历字符串,准备一个哈希表,key存放遍历过的字符,value存放它最后出现过的位置,准备一个int变量pre,代表以当前位置前一个位置结尾时最长的无重复子字符串长度。当来到i位置,首先在哈希表内检查这个字符是否出现过,如果没有,则当前位置的最长长度 = pre + 1。如果当前字符在之前出现过,那么要看以i-1位置上的字符结尾的最长的无重复子字符串的开头位置pos1与上一次出现当前字符的位置pos2谁距离i位置更近,如果是前者,则当前位置的最长长度 = pre + 1,如果是后者,那么当前位置的最长长度 = i - pos2 + 1。更新完当前位置的dp值后要把当前位置字符出现的位置在哈希表内也更新,最后遍历完字符串,dp值最大的就是结果。
int longest(string str)
{
if (str.size() == 0)
{
return 0;
}
unordered_map<char, int> map;
map.insert(make_pair(str[0], 0));
int maxLength = 1;
int pre = 1;
int cur = 0;
for (int i = 1; i < str.size(); i++)
{
if (map.count(str[i]) == 0)
{
cur = pre + 1;
map.insert(make_pair(str[i], i));
}
else
{
cur = i - max(map.at(str[i]), i - pre);
map.at(str[i]) = i;
}
maxLength = max(cur, maxLength);
pre = cur;
}
return maxLength;
}
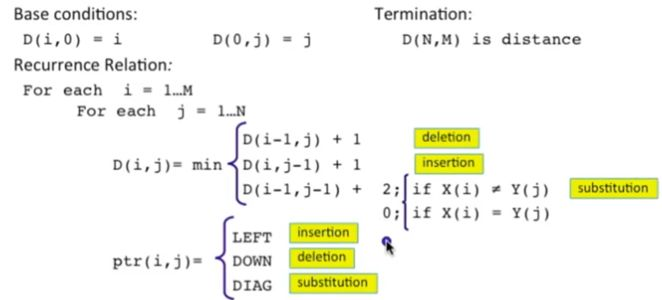
题目6(编辑距离问题,比较重要,硬记也要记住)
给定两个字符串str1和str2,再给定三个整数ic、dc和rc,分别代表插入、删除和替换一个字符的代价,返回将str1编辑成str2的最小代价。
[举例]
str1="abc",str2=" adc",ic=5, dc=3, rc=2
从"abc"编辑成"adc",把'b'替换成'd'是代价最小的,所以返回2
str1="abc",str2="adc",ic=5,dc=3,rc=100
从"abc "编辑成"adc",先删除'b',然后插入'd'是代价最小的,所以返回8
str1="abc",str2="abc",ic=5,dc=3,rc=2
不用编辑了,本来就是一样的字符串,所以返回0
思路
网上帖子很多,有心情就看,没心情就硬记。罗列四种可能性(也可以说三大种,后面两种属于一个类),取最小值。
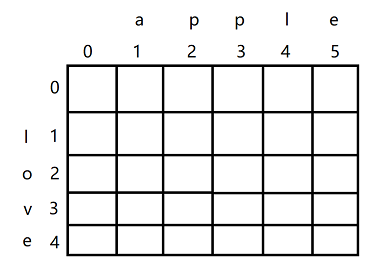
准备一个表格,行列分别代表str1和str2的字符,谁是行谁是列无所谓,不过是从0开始,1代表str1和str2的第一个字符。假设str1="love",str2="apple",就像下面一样
表格内的值有什么含义?假设表格叫dp,dp[i][j]代表从str1的前0-i个字符变化到str2的前0-j个字符所需要的代价。base case就是i和j分别为0的时候,i为0,就是每次加上一个字符,dp第一行的值就是ic*0,ic*1,ic*2,ic*3......。j为0,就是删除一、二、三...个字符,dp第一行的值就是dc*0,dc*1,dc*2,dc*3......。这样base case就填好了。那么普遍位置的值怎么求?罗列第一张图中描述的四种可能性
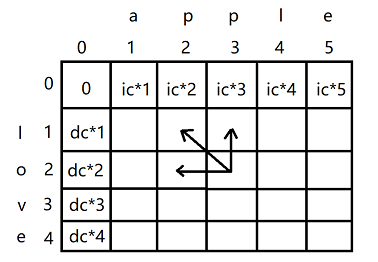
如上图,普遍位置与它左、上、左上三个格子有关。先看左上角,如果i位置上的字符(图中代表2位置'o'),与j位置上的字符(图中代表2位置的'p')不相等,要想从str1的前0-i个字符变化到str2的前0-j个字符,则需要左上角的格子的值(0-i-1变化为0-j-1)再加上一个替换字符的代价,即dp[i-1][j-1]+rc;如果i与j位置上的字符相等,则不需要加上替换的代价,即dp[i-1][j-1]。再看左边的格子,是从str1的前0-i个字符变化为str2的前0-j-1个字符的代价,如果想要完整的变化,则需要再加上插入一个字符的代价(插入j位置的字符),即dp[i][j-1]+ic。再看上方的格子,是从str1的前0-i-1个字符变化为str2的前0-j个字符的代价,如果想要完整的变化,则需要再加上删除一个字符的代价(插入i位置的字符),即dp[i][j-1]+dc。自此可能性罗列完毕,dp[i][j]的值就是dp[i][j-1]+ic、dp[i][j-1]+dc、(i位置上的字符与j位置(这里的i位置的字符、j位置的字符不是str[i]和str[j],应是str[i-1]和str[j-1])上的字符相等时取dp[i-1][j-1],不等时取dp[i-1][j-1]+rc),这三个值之间的最小值。把表中的格子按照从上到下、从左到右的顺序填完后返回dp[str1.size()][str2.size()]即可。
int minDistance(string str1, string str2, int ic, int dc, int rc)
{
int N = str1.size();
int M = str2.size();
vector<vector<int>> dp(N + 1, vector<int>(M + 1));
for (int i = 1; i < N + 1; i++)
{
dp[i][0] = i * dc;
}
for (int i = 1; i < M + 1; i++)
{
dp[0][i] = i * ic;
}
for (int i = 1; i < N + 1; i++)
{
for (int j = 1; j < M + 1; j++)
{
if (str1[i - 1] == str2[j - 1])
{
dp[i][j] = dp[i - 1][j - 1];
}
else
{
dp[i][j] = dp[i - 1][j - 1] + rc;
}
dp[i][j] = min(dp[i - 1][j] + dc, dp[i][j]);
dp[i][j] = min(dp[i][j - 1] + ic, dp[i][j]);
}
}
return dp[N][M];
}
题目7
给定一个全是小写字母的字符串str,删除多余字符,使得每种字符只保留一个,并让最终结果字符串的字典序最小
[举例]
str = "acbc",删掉第一个'c',得到"abc",是所有结果字符串中字典序最小的。
str = "dbcacbca",删掉第一个'b'、第一个'c'、第二个'c'、第二个'a',得到"dabc",是所有结果字符串中字典序最小的。
思路
首先遍历一遍字符串,建立词频表。然后再从头开始遍历,每遍历一个字符,就把它在词频表中的记录-1。当第一次有一个字符的词频变为0时,假设当前位置是i,我们可以知道在0~i范围内选定任意一个字符,然后把它前面的字符全部删掉,得到的结果仍然可以保证不会缺失字符的种类。那么选择哪一个位置的字符呢?因为题干要求最后的结果字典序最小,所以选择0~i位置上字典序最小的字符(即ASCII码最小的),如果有多个字典序最小的字符,则选择下标最小的那个。假设选择的下标是j,字符是a,那么把0~j-1位置上的字符全部删掉,同时删掉整个字符串str中的a,这时最后的结果第一个字符就是a,删完剩下的字符递归进行前面的过程,每次选出一个字符加到a后面,最后字符串为空结束,返回最后的结果。
string delStr(string str, int index, char cha); //删除0\~index-1位置上的字符,再删除str中的cha字符
string minDictionaryOrder(string str)
{
if (str.size() == 0)
{
return "";
}
unordered_map<char, int> charFreq;
for (int i = 0; i < str.size(); i++)
{
if (charFreq.count(str[i]) == 0)
{
charFreq.insert(make_pair(str[i], 1));
}
else
{
charFreq.at(str[i])++;
}
}
int del = 0;
string res = "";
for (int i = 0; i < str.size(); i++)
{
if (str[del] > str[i])
{
del = i;
}
if ((--charFreq.at(str[i])) == 0)
{
return str[del] + minDictionaryOrder(delStr(str, del, str[del]));
}
}
}
string delStr(string str, int index, char cha)
{
string resTmp = "";
string res = "";
for (int i = index + 1; i < str.size(); i++)
{
resTmp += str[i];
}
for (int i = 0; i < resTmp.size(); i++)
{
if (resTmp[i] != cha)
{
res += resTmp[i];
}
}
return res;
}
题目8
在数据加密和数据压缩中常需要对特殊的字符串进行编码。给定的字母表A由26个小写英文字母组成,即A={a,b...z}。该字母表产生的长序字符串是指定字符串中字母从左到右出现的次序与字母在字母表中出现的次序相同,且每个字符最多出现1次。例如:a,b,ab,bc,xyz等字符串是升序字符串。对字母表A产生的所有长度不超过6的升序字符串按照字典排列编码如下: a(1),b(2),c(3)...,z(26),ab(27),ac(28)...
对于任意长度不超过16的升序字符串,迅速计算出它在上述字典中的编码。
思路
题干看起来太复杂,简单来说要求是字符串必须是字母表A的子序列,例如不会出现ba这样的字符串,因为字母表A中a在b的前面,ba不是A的子序列。所有子序列按照字典序排序的结果就是上述字典中从编码1到最后排序的结果。
如何求得一个子序列的编码?整体思路就是找出当前子序列前面所有子序列的个数,这个个数再+1就是当前子序列的编码。假设当前子序列为str,长度为N,那么所有长度为N-1的子序列都再它的前面。其次,所有以字典序小于str[0]的字母开头的长度为N的子序列也都在当前子序列的前面。看完str[0]我们接着看str[1],所有以str[0]开头的、以字典序小于str[1]的字母作为第二个字符的长度为N的子序列都在当前子序列前面,即以字典序小于str[1]、大于str[0]的字母作为开头的长度为N-1的子序列。接着就是所有以字典序小于str[2]、大于str[1]的字母作为开头的长度为N-2的子序列......。一直累加到所有以字典序小于str[N-1]、大于str[N-2]的字母作为开头的长度为1的子序列。最后的结果就是累加的结果+1。
那么问题就来了,根据上面的流程,我们需要知道任意长度的所有子序列的个数、以某个字母开头任意长度的所有子序列的个数。我们先看后面那个怎么求,需要用到递归,base case是长度为1,因为要求是某个特定字母开头,所以返回结果是1。下面就是累加以a~z开头的长度为当前长度-1的子序列个数。那么任意长度的所有子序列的个数怎么求?其实就是分别以a~z开头长度为当前长度的子序列个数的和,可以调用前面那个函数。代码如下:
int g(int i, int len) //以i开头,总长度为len的子序列个数
{
if (len == 1)
{
return 1;
}
int sum = 0;
for (int j = i + 1; j <= 26; j++)
{
sum += g(j, len - 1);
}
return sum;
}
int f(int len) //长度为len的子序列个数
{
int sum = 0;
for (int i = 1; i <= 26; i++)
{
sum += g(i, len);
}
return sum;
}
题解代码:
int kth(string s)
{
int sum = 0;
for (int i = 1; i <= s.size() - 1; i++)
{
sum += f(i);
}
for (int j = 1; j <= s[0] - 'a'; j++)
{
sum += g(j, s.size());
}
int pre = s[0] - 'a' + 1;
for (int i = 1; i < s.size(); i++)
{
for (int j = pre + 1; j <= s[i] - 'a'; j++)
{
sum += g(j, s.size() - i);
}
pre = s[i] - 'a' + 1;
}
return sum + 1;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号