算法提升(5):斐波那契数列套路O(logN)优化
适用问题
题目的本质是类似于求斐波那契数列第N项的值或者需要这样一个过程的问题
满足条件
所求的第N项满足下面这样的严格递推式
F(N) = a * F(N - 1) + b * F(N - 2) + c * F(N - 3) + . . . . . . + x * F(N - y)
优化原理
- 首先根据线性代数的知识我们可以得到这样一个关系式(下面画横线的表示也是矩阵)
![]()
- 将F(y+1)开始一直到F(N)为止的式子写出来,然后前面的式子代入到后面式子,可以得到以下结果
![]()
- 那么现在的问题就是如何求得这个y阶矩阵,以及如何快速求出矩阵的某次幂。
如何求得这个y阶矩阵
这个矩阵一共有y2个未知数,其实就是求y2元一次方程的解,因为我们可以根据递推公式轻易地求出前面某些项的值,代入即可求出这个y阶矩阵。这里求解的过程是在草稿纸上进行的,不必写在代码里,因为每一题都有特定的y阶矩阵,且每一题中是固定的,自己手动求出直接用即可。
如何快速求出矩阵的某次幂
这里用到了矩阵的快速幂,将幂转换成2进制数,准备一个单位矩阵(相当于十进制的1)和矩阵的1次方,从二进制数的最右边开始,如果这一位是1,则把当前矩阵累乘到单位矩阵上,然后当前矩阵累乘自己,二进制数右移一位;如果是0则单位矩阵不累乘当前矩阵,当前矩阵累乘自己,二进制数右移一位。直到右移到0。这样的求法是O(logN)级别的,因为除了求出y阶矩阵的N-y次幂,其他操作都是O(1)水平的,所以就把整个算法的时间复杂度降低到了O(logN)。这就是斐波那契数列套路
应用案例
求斐波那契数列的第N项值。
int fib(int n) {
if(n == 0)
{
return 0;
}
else if(n == 1 || n == 2)
{
return 1;
}
int MOD = 1000000007;
vector<vector<int>> matrix = {{1, 1}, {1, 0}}; //已经提前求好的y阶矩阵
matrix = pow(matrix, n - 2);
return (matrix[0][0] + matrix[1][0]) % MOD;
}
vector<vector<int>> pow(vector<vector<int>> matrix, int n) //快速幂
{
vector<vector<int>> ans(matrix.size(), vector<int>(matrix[0].size()));
for(int i = 0; i < ans.size(); i++)
{
ans[i][i] = 1;
}
while(n != 0)
{
if(n & 1)
{
ans = mutilMatrix(ans, matrix);
}
matrix = mutilMatrix(matrix, matrix);
n = n >> 1;
}
return ans;
}
vector<vector<int>> mutilMatrix(vector<vector<int>>& matrix1, vector<vector<int>>& matrix2) //矩阵乘法
{
int MOD = 1000000007;
vector<vector<int>> ans(matrix1.size(), vector<int>(matrix2[0].size()));
for(int i = 0; i < ans.size(); i++)
{
for(int j = 0; j < ans[0].size(); j++)
{
ans[i][j] += (int)(((long)matrix1[i][0] * matrix2[0][j] + (long)matrix1[i][1] * matrix2[1][j])%MOD);
}
}
return ans;
}


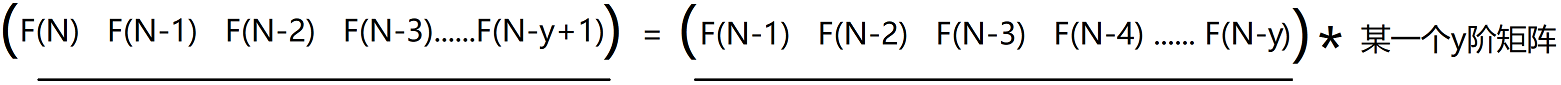
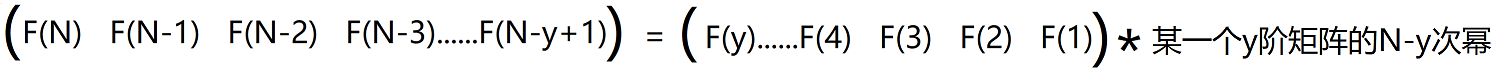

 浙公网安备 33010602011771号
浙公网安备 33010602011771号