算法提升(4):栈和队列的应用(返回栈内最小元素、栈改队列,队列改栈)、dp的空间压缩技巧、流程优化(接雨水、数字前后部分最大值的最大差值)、KMP算法的应用、咖啡杯问题、四的倍数问题
栈和队列的应用
题目1
实现一个特殊的栈,在实现栈的基本功能的基础上,再实现返回栈中最小元素的操作。要求:
- pop、push、getMin操作的时间复杂度都是0(1);
- 设计的栈类型可以使用现成的栈结构
思路
准备两个栈,一个站作为正常进出的栈,另一个栈为辅助栈。当正常栈与辅助栈同时入栈同时出栈,但是辅助栈入栈时判断当前入栈元素是否比辅助栈栈顶元素小,如果是则正常入栈,如果比栈顶元素大,则不入栈当前元素,改为把栈顶的较小的元素拷贝一份入辅助栈,当需要返回最小元素时,把辅助栈栈顶返回即可,但是注意正常栈出栈时辅助栈也跟着弹出元素。
class GetMinStack
{
public:
void push(int i)
{
s1.push(i);
if (s2.empty())
{
s2.push(i);
}
else
{
int curMin = s2.top();
if (curMin > i)
{
s2.push(i);
}
else
{
s2.push(curMin);
}
}
}
int pop()
{
if (!s1.empty())
{
int temp = s1.top();
s1.pop();
s2.pop();
return temp;
}
else
{
throw "STACK IS EMPTY!";
}
}
int getMin()
{
if (!s2.empty())
{
return s2.top();
}
else
{
throw "STACK IS EMPTY!";
}
}
private:
stack<int> s1;
stack<int> s2;
};
题目2
如何仅用队列结构实现栈结构
思路
准备两个队列,分别为队列1和队列2。两个队列交替使用,当有元素要进栈时,进队列1,要出栈时,把队列1除了最后进队列的元素其他元素全都进队列2,把队列1的最后一个元素弹出队列就相当于出栈,然后想要进栈就开始进队列2,当又要出栈时,就跟前面的步骤一样,只不过反过来,把队列2里除了最后一个元素都进队列1,把最后一个元素弹出。就这样两个队列交替使用实现栈结构
class QueueToStack
{
public:
QueueToStack()
{
isQ1 = true; //初始值为true
}
void push(int i)
{
if (isQ1)
{
q1.push(i);
}
else
{
q2.push(i);
}
}
int pop()
{
if (isQ1 && !q1.empty())
{
for (int i = 0; i < q1.size() - 1; i++)
{
int temp = q1.front();
q1.pop();
q2.push(temp);
}
int top = q1.front();
q1.pop();
isQ1 = false; //弹出后下次进栈改为进队列2
return top;
}
if (!isQ1 && !q2.empty())
{
for (int i = 0; i < q2.size() - 1; i++)
{
int temp = q2.front();
q2.pop();
q1.push(temp);
}
int top = q2.front();
q2.pop();
isQ1 = true; //弹出后下次进栈改为进队列1
return top;
}
throw "STACK IS EMPTY!";
}
int peek()
{
if (isQ1 && !q1.empty())
{
return q1.back();
}
else if(!isQ1 && !q2.empty())
{
return q2.back();
}
else
{
throw "STACK IS EMPTY!";
}
}
private:
queue<int> q1;
queue<int> q2;
bool isQ1; //如果要进栈是否进q1
};
题目3
如何仅用栈结构实现队列结构
思路
准备两个栈,一个push栈,一个pop栈,push栈进元素,pop栈弹出元素。当进队列时,进push栈;当从队的头出元素时,先检查pop栈是否为空,如果为空,则把push栈内的所有元素都进pop栈,弹出pop栈栈顶元素;如果pop栈不为空,则从pop栈弹出栈顶元素,push栈不动
class StackToQueue
{
public:
void push(int i)
{
pushStack.push(i);
moveIntoPop();
}
int pop()
{
if (popStack.empty() && pushStack.empty())
{
throw "QUEUE IS EMPTY!";
}
else
{
moveIntoPop();
int temp = popStack.top();
popStack.pop();
return temp;
}
}
int front()
{
if (popStack.empty() && pushStack.empty())
{
throw "QUEUE IS EMPTY!";
}
else
{
moveIntoPop();
return popStack.top();
}
}
private:
void moveIntoPop()
{
if (popStack.empty())
{
while (!pushStack.empty())
{
int temp = pushStack.top();
popStack.push(temp);
pushStack.pop();
}
}
}
private:
stack<int> pushStack;
stack<int> popStack;
};
动态规划的空间压缩技巧
假设有一个动态规划的dp表位置依赖如下图所示
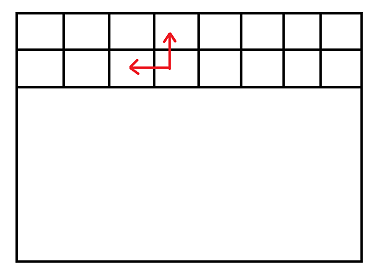
此类位置依赖的动态规划其实不需要一整张表,只需要以dp表列长度为数组长度的一维数组即可,循环往下滚动更新。
题目4
给你一个二维数组matrix,其中每个数都是正数,要求从左上角走到右下角。每一步只能向右或者向下,沿途经过的数字要累加起来。最后请返回最小的路径和。
递归思路
从左上到右下,每次都可以往下或往右,没到右边界和下边界之前,返回两种选择路径和最小的,到了右边界就返回往下走的路径和,到了下边界就返回往右走的路径和。base case是到了矩阵右下角,返回右下角的值。
int process(vector<vector<int>> matrix, int row, int col);
int minPathSum(vector<vector<int>> matrix)
{
if (matrix.size() == 0 || matrix[0].size() == 0)
{
return 0;
}
return process(matrix, 0, 0);
}
int process(vector<vector<int>> matrix, int row, int col)
{
if (row == matrix.size() - 1 && col == matrix[0].size() - 1)
{
return matrix[row][col];
}
if (row < matrix.size() - 1 && col < matrix[0].size() - 1)
{
return min(matrix[row][col] + process(matrix, row + 1, col), matrix[row][col] + process(matrix, row, col + 1));
}
else if (row < matrix.size() - 1)
{
return matrix[row][col] + process(matrix, row + 1, col);
}
else
{
return matrix[row][col] + process(matrix, row, col + 1);
}
}
动态规划
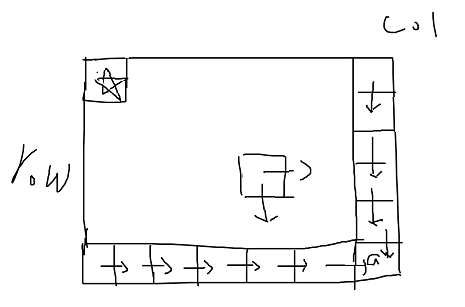
dp表如下图,右下角的值a为base case,即要求最短路径和的矩阵的右下角的值。位置依赖如箭头所示,最后一行都依赖于自己右边的格子,最后一列都依赖于自己下面的格子,一般位置依赖于自己下面和右面的格子。这种位置依赖模型可以用空间压缩,一维数组即可完成动态规划。
int minPathSum(vector<vector<int>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0)
{
return 0;
}
int row = matrix.size();
int col = matrix[0].size();
vector<int> dp(col);
dp[col - 1] = matrix[row - 1][col - 1];
for (int i = col - 2; i >= 0; i--)
{
dp[i] = matrix[row - 1][i] + dp[i + 1];
}
for (int i = row - 2; i >= 0; i--)
{
for (int j = col - 1; j >= 0; j--)
{
if (j == col - 1)
{
dp[j] = matrix[i][j] + dp[j];
}
else
{
dp[j] = min(matrix[i][j] + dp[j + 1], matrix[i][j] + dp[j]);
}
}
}
return dp[0];
}
流程优化
流程的优化从两方面入手:1.数据状况,2.所求答案的标准
题目5(接雨水,从所求答案的标准进行优化)
给定一个数组arr,已知其中所有的值都是非负的,将这个数组看作一个容器,请返回容器能装多少水
比如,arr={3, 1, 2, 5, 2, 4},根据值画出的直方图就是容器形状,该容器可以装下5格水
再比如,arr={4, 5, 1, 3, 2},该容器可以装下2格水
思路
与洗衣机问题类似,考虑单个位置的情况,如果我当前在i位置,我左边的最大值与右边的最大值都比我大,那么我的上方一定可以接到雨水,不管我旁边的值比我小还是比我大,因为我知道左右两边一定有比我大的可以挡住我上方的雨水,而接到的雨水就是左右两边最大值较小的那个高度减去我的高度。而其它情况比如我比左右两边的最大值其中一个大,那么我就接不到雨水。这样把所有位置上方能接到的雨水都求出来然后相加就是答案。依据这种思路你当然可以采用预处理数组的方式把每个位置左右两边的最大值求出来,然后主过程直接拿值,这样虽然时间复杂度还是O(N),但是额外空间复杂度也是O(N),能不能有一种方法只需要O(1)的额外空间复杂度。
答案是可以的。准备两个指针,left代表当前要遍历的左边的位置,right代表当前要遍历的右边的位置。再准备两个指针,leftMax代表左边已经遍历过的值中最大的值的下标,rightMax代表右边已经遍历过的值中最大的值的下标。准备一个变量ans代表总水量,初始值是0。数组最左边的位置和最右边的位置都接不到水,所以从数组第二位和倒数第二位开始算起,所以left的初始值设为1,right的初始值设为arr.size()-2,leftMax的初始值设为0,rightMax的初始值设为arr.size()-2。因为数组的size小于3的情况无论如何都接不到水直接返回0,所以不用考虑left和right的初始值越界的问题。我们现在开始遍历,原则是先更新左右两边最大值较小的那一边,因为较小的那一边是实实在在遍历过一遍已经确认过的最大值,而另一边可能还会更大。更新时看当前位置是否比arr[leftMax]和arr[rightMax]都要小,如果是,则可以接到雨水,更新ans,当前选择更新的一边如果是left就left++,如果是right就right--;如果没有比arr[leftMax]和arr[rightMax]都小,那么就代表当前位置至少要比两者其中一个大或者相等,那么至少会比哪个大或者相等呢,答案是最大值较小的那个,因为我们已经判断过要更新这边,选择更新这边的前提就是这边的最大值较小,而较小的最大值是实实在在遍历过且确定的最大值,不可能最大值还要大,而当前位置比这个最大值还要大或相等,那么此时一定接不住雨水,所以ans不变,当前选择更新的一边如果是left就left++,leftMax更新,如果是right就right--,rightMax更新。直到left大于right停止遍历。
int trap(vector<int>& arr)
{
if (arr.size() < 3)
{
return 0;
}
int L = 1;
int R = arr.size() - 2;
int LMax = 0;
int RMax = arr.size() - 1;
int ans = 0;
while (L <= R)
{
if (arr[LMax] < arr[RMax]) //哪边已经遍历过的最大值较小就更新哪边
{
ans += arr[L] < arr[LMax] && arr[L] < arr[RMax] ? arr[LMax] - arr[L] : 0; //判断是因为能接到雨水更新还是因为接不到雨水更新
LMax = arr[LMax] > arr[L] ? LMax : L; //判断最大值是否需要更新
L++;
}
else
{
ans += arr[R] < arr[LMax] && arr[R] < arr[RMax] ? arr[RMax] - arr[R] : 0;
RMax = arr[RMax] > arr[R] ? RMax : R;
R--;
}
}
return ans;
}
题目6(从所求答案的标准进行优化)
给定一个数组arr长度为N,你可以把任意长度大于0且小于N的前缀作为左部分,剩下的作为右部分。但是每种划分下都有左部分的最大值和右部分的最大值。请返回最大的,左部分最大值减去右部分最大值的绝对值。
思路
题意是你可以把数组任意分成两部分,但是必须保证两边都要有东西。优化前的思路是你可以利用预处理数组,遍历两边数组分别记录每种分割法左边的最大值和右边的最大值,然后再遍历一遍数组找最大的绝对值,这种方式时间复杂度是O(N),额外空间复杂度也是O(N),但是真的有必要遍历三遍数组吗?
答案是不需要,我们可以这样想,想要让左右两边最大值的差值的绝对值尽量大,那么就需要知道数组中的最大值,和它相减才能最大,这样就变成了找最小的最大值。第一种情况是数组的最大值作为左部分,那么需要找到右部分最小的最大值,但是不管你把分界线怎么移动,总会有数组中最后一个值在右部分,你不可能摆脱它,所以当右部分只有数组中最后一个值的时候,就是最小的最大值。同理最大值在右部分时,左部分只有数组中第一个值的时候是最小的最大值。这样就变成了遍历一遍数组找到数组中的最大值,然后看它与数组中的第一个值与最后一个值的差值谁大的问题。
int maxDifference(vector<int> &arr)
{
if (arr.size() < 2)
{
return 0;
}
int maxValue = INT_MIN;
for (int i = 0; i < arr.size(); i++)
{
maxValue = maxValue < arr[i] ? arr[i] : maxValue;
}
return max(maxValue - arr[arr.size() - 1], maxValue - arr[0]);
}
KMP算法的应用
题目7
如果一个字符串为str,把字符串str前面任意的部分挪到后面形成的字符串叫作str的旋转词。比如str=" 12345",str 的旋转词有"12345"、"23451"、"34512"、"45123"和"51234"。给定两个字符串a和b,请判断a和b是否互为旋转词。
比如:
a="cdab",b="abcd",返回true。
a="1ab2",b="ab12",返回false。
a=" 2ab1",b="ab12",返回true。
思路
看b是否是a+a的子串。如果是,那么a和b就互为旋转词。因为如果你把一个字符串加上自己,那么它所有的旋转词就都会包含在里面。
vector<int> getNextArr(string str);
bool isRevolvingWords(string str1, string str2)
{
if (str1.size() == 0 || str2.size() == 0 || str1.size() != str2.size())
{
return false;
}
str1 = str1 + str1;
vector<int> next = getNextArr(str2);
int i1 = 0;
int i2 = 0;
while (i1 < str1.size() && i2 < str2.size())
{
if (str1[i1] == str2[i2])
{
i1++;
i2++;
}
else if(next[i2] == -1)
{
i1++;
}
else
{
i2 = next[i2];
}
}
return i2 == str2.size();
}
vector<int> getNextArr(string str)
{
vector<int> next(str.size());
next[0] = -1;
int cn = 0;
int i = 2;
while (i < next.size())
{
if (str[i - 1] == str[cn])
{
next[i] = next[i - 1] + 1;
}
else if(cn > 0)
{
cn = next[cn];
}
else
{
i++;
}
}
return next;
}
题目8(咖啡机问题,贪心+动态规划)
给你如下数据:
数组arr:数组长度表示一共有几台咖啡机,数组中的数值代表每台咖啡机各自制作一杯咖啡需要的时间,例如arr=[3,2,7]就表示一共有三台咖啡机,第一台咖啡机制作一杯咖啡需要3单位时间,第二台需要2单位时间,第三台需要7单位时间。
int N:表示有N个人需要用咖啡机制作咖啡,每人一杯,同时,假设制作完咖啡后,喝咖啡时间为0。
int a:表示用洗碗机洗一个咖啡杯需要的时间,只有一台,每次只洗一个咖啡杯。
int b:表示咖啡杯也可以不洗,自然晾干的时间。咖啡杯要么洗,要么晾干。
现在,请你求出这N个人从开始用咖啡机制作咖啡到所有杯子洗好或者晾干的最少时间?
思路
首先解决第一个问题,这N个人如何泡咖啡能最快。定义一个咖啡机类,里面存放两个数据项,第一个是可用时间availableTime,代表在第几个时刻这台咖啡机可以被使用,第二个是这台咖啡机制作一杯咖啡需要的时间time。准备一个小根堆维护咖啡机,内部按availableTime + time的大小组织,这样做之后小根堆堆顶的咖啡机就是下一次最早时刻做出一杯咖啡的咖啡机。准备一个大小为N的数组arr,从下标为0的人开始,一直到下标为N-1的人,每次从小根堆堆顶弹出咖啡机,availableTime更新为availableTime + time再放回小根堆,arr[i] = availableTime + time代表第i个人喝完咖啡的时间。这样下来arr就是每个人喝完咖啡的时间,也就是咖啡杯需要开始被清洗或晾干的时间。
那么如何选择是用洗碗机洗还是自然晾干呢,可以采用递归或动态规划的方式。递归思路讲解https://www.bilibili.com/video/BV13g41157hK?p=24&vd_source=77d06bb648c4cce91c6939baa0595bcd P24 01:24:16
递归代码:
class CoffeeMachine
{
public:
CoffeeMachine(int availableTime, int time)
{
this->availableTime = availableTime;
this->time = time;
}
public:
int availableTime;
int time;
};
class CoffeeMachineCompare
{
public:
bool operator()(CoffeeMachine cm1, CoffeeMachine cm2)
{
return (cm1.availableTime + cm1.time) > (cm2.availableTime + cm2.time);
}
};
int washCap1(vector<int> overDrinkTime, int a, int b, int index, int available);
int coffeeCapMinTime(vector<int> arr, int N, int a, int b)
{
if (arr.size() < 0 || N < 0 || a < 0 || b < 0)
{
return -1;
}
priority_queue<CoffeeMachine, vector<CoffeeMachine>, CoffeeMachineCompare> EarliestCoffeeMachinHeap;
for (int i = 0; i < arr.size(); i++)
{
CoffeeMachine temp(0, arr[i]);
EarliestCoffeeMachinHeap.push(temp);
}
vector<int> overDrinkTime(N);
for (int i = 0; i < N; i++)
{
CoffeeMachine EarliestCoffeeMachine = EarliestCoffeeMachinHeap.top();
EarliestCoffeeMachinHeap.pop();
EarliestCoffeeMachine.availableTime += EarliestCoffeeMachine.time;
overDrinkTime[i] = EarliestCoffeeMachine.availableTime;
EarliestCoffeeMachinHeap.push(EarliestCoffeeMachine);
}
return washCap1(overDrinkTime, a, b, 0, 0);
}
int washCap1(vector<int> overDrinkTime, int a, int b, int index, int available)
{
if (index = overDrinkTime.size() - 1)
{
return min(overDrinkTime[index] + b, max(available, overDrinkTime[index]) + a);
}
int wash = max(available, overDrinkTime[index]) + a;
int allOver1 = washCap1(overDrinkTime, a, b, index + 1, wash);
int p1 = max(wash, allOver1);
int dry = overDrinkTime[index] + b;
int allOver2 = washCap1(overDrinkTime, a, b, index + 1, available);
int p2 = max(dry, allOver2);
return min(p1, p2);
}
动态规划代码
int coffeeCapMinTime2(vector<int> arr, int N, int a, int b)
{
if (arr.size() < 0 || N < 0 || a < 0 || b < 0)
{
return -1;
}
priority_queue<CoffeeMachine, vector<CoffeeMachine>, CoffeeMachineCompare> EarliestCoffeeMachinHeap;
for (int i = 0; i < arr.size(); i++)
{
CoffeeMachine temp(0, arr[i]);
EarliestCoffeeMachinHeap.push(temp);
}
vector<int> overDrinkTime(N);
for (int i = 0; i < N; i++)
{
CoffeeMachine EarliestCoffeeMachine = EarliestCoffeeMachinHeap.top();
EarliestCoffeeMachinHeap.pop();
EarliestCoffeeMachine.availableTime += EarliestCoffeeMachine.time;
overDrinkTime[i] = EarliestCoffeeMachine.availableTime;
EarliestCoffeeMachinHeap.push(EarliestCoffeeMachine);
}
if (a >= b)
{
return overDrinkTime[N - 1] + b;
}
vector<vector<int>> dp(N, vector<int>(overDrinkTime[N - 1] + N * a));
for (int i = 0; i < dp[0].size(); i++)
{
dp[N - 1][i] = min(overDrinkTime[N - 1] + b, max(i, overDrinkTime[N - 1]) + a);
}
for (int i = N - 2; i >= 0; i--)
{
int available = overDrinkTime[i] + (i + 1) * a;
for (int j = 0; i < available; j++)
{
int wash = max(j, overDrinkTime[i]) + a;
int allOver1 = dp[i + 1][wash];
int p1 = max(wash, allOver1);
int dry = overDrinkTime[i] + b;
int allOver2 = dp[i + 1][j];
int p2 = max(dry, allOver2);
dp[i][j] = min(p1, p2);
}
}
return dp[0][0];
}
题目9
给定一个数组arr,如果通过调整可以做到arr中任意两个相邻的数字相乘是4的倍数,返回true;如果不能返回false
思路
先统计数组中三种数的数量,第一种是奇数的个数a,第二种是2的倍数但不是4的倍数的数的个数b,第三种是4的倍数的数c,分情况讨论
- 如果b=0。只有奇数和4的倍数,那么就需要消耗4的倍数的个数去与奇数配对,消耗最少的方式是一个奇数、一个4的倍数、一个奇数…………。所以a=1时,要求c>=1;当a>1时,c>=a-1。
- 如果b≠0。那么b中的所有数挨着排就所有的数字相乘都是4的倍数,不用消耗4的倍数的个数。这种情况还有以下分类
(1)a=0,b=1。c>=1才能满足要求,因为当只有一个二的倍数时,必须要有一个四的倍数与它配对。
(2)a=0,b≠1。c可以是任意数量
(3)a≠0。需要一个4的倍数作为衔接2的倍数部分与奇数部分的桥梁,因为最后一个2的倍数没办法与奇数相乘得到4的倍数,后面奇数与4的倍数的排列就与b=0情况一样,所以这种情况需要c>=a。
bool isMultipleOfFour(vector<int> arr)
{
int a = 0;
int b = 0;
int c = 0;
for (int i = 0; i < arr.size(); i++)
{
if (arr[i] % 4 == 0)
{
c++;
}
else if (arr[i] % 2 == 0)
{
b++;
}
else
{
a++;
}
}
if (b == 0)
{
if (a == 1)
{
return c >= 1;
}
else
{
return c >= a - 1;
}
}
else
{
if (b == 1 && a == 0)
{
return c >= 1;
}
if (a > 0)
{
return c >= a;
}
return true;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号