算法提升(1):窗口不回退模型、打表法、预处理数组、返回a~b的随机函数改c~d的随机函数
三个技巧
窗口不回退模型
题目
给定一个有序数组arr,代表数轴上从左到右有n个点arr[0]、arr[1]...arr[n-1],给定一个正数L,代表一根长度为L的绳子,求绳子最多能覆盖其中的几个点。
思路一
从左到右,当来到数组i位置的时候,计算arr[i]-L的值,二分查找数组0~i之间大于等于arr[i]-L的值,i的减去这个值的下标再加1就是i位置左侧能够包含最多的点,遍历数组并找到最大的就是要求的值。
思路二
窗口,L与R之间不能超过绳子的长度,初始时L与R都在0位置,num记录覆盖的点的个数,初始时为1,max记录目前覆盖最多的点,初始值为0。R尝试往右移动,此时开始计算L与R+1之间的距离(即L与R+1各自在数组中对应的值的差)有没有超过绳子的长度以及R移动后会不会越界,如果没超过且不越界则num++,R往右移动一位。继续判断L与R+1之间的距离有没有超过绳子的长度且越不越界,没有R就继续往右移动,直到超过绳子的长度或越界,R和num不变,max与num比较并更新,L往右移动一次,num-1。重复前面的过程,直到L移动到数组最后的位置,最后返回max
int maxSpots(vector<int> arr, int L)
{
int left = 0;
int right = 0;
int num = 1;
int max = 0;
while (left < arr.size())
{
while (right < arr.size() - 1 && arr[right + 1] - arr[left] <= L)
{
num++;
right++;
}
max = max < num ? num : max;
left++;
num--;
}
return max;
}
打表法
输入参数是整数,输出参数是整数(或者字符等很简单的类型),先写一个简单的最容易想的解法,然后利用对数器输出一个很大范围上的结果,看输出的结果有什么规律,根据这种规律,输入什么按照规律直接输出结果
题目1
小虎去附近的商店买苹果,奸诈的商贩使用了捆绑交易,只提供6个每袋和8个每袋的包装包装不可拆分。可是小虎现在只想购买恰好n个苹果,小虎想购买尽量少的袋数方便携带。如果不能购买恰好n个苹果,小虎将不会购买。输入一个整数n,表示小虎想购买的个苹果,返回最小使用多少袋子。如果无论如何都不能正好装下,返回-1。
普通解法
思路:先拿尽量多的8,假设n/8=m,先看看n-8m的结果能不能被6整除,不能就看n-8(m-1)的结果能不能被6整除,如果还是不能就m-2,一直减下去,直到m为0还不能则返回-1。
int apples(int n)
{
int m = n / 8;
for (int i = m; i >= 0; i--)
{
if ((n - i * 8) % 6 == 0)
{
return i + ((n - i * 8) / 6);
}
}
return -1;
}
经过一次优化的思路
其实当上面的(n-i*8) > 24后还不能被6整除就不用再尝试了,因为剩余苹果数为(n-i*8)-24的情况前面已经被求过了。
//优化后代码
int apples2(int n)
{
if (n < 0 || n % 2 != 0)
{
return -1;
}
int m = n / 8;
while (m >= 0 && (n - m * 8) <= 24)
{
if ((n - m * 8) % 6 == 0)
{
return m + ((n - m * 8) / 6);
}
m--;
}
return -1;
}
打表法
输出输入参数从0到99的结果,看规律
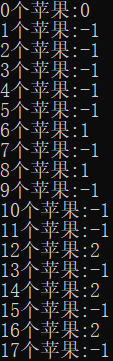


0 ~ 17规律并不明显,从18开始,3与-1交替出8次,然后4与-1交替出现8次,然后是5,然后是6,以次类推
//打表法代码
int apples3(int n)
{
if (n < 0 || n % 2 != 0)
{
return -1;
}
if (n < 18)
{
return n >= 12 ? 2 : (n == 0 ? 0 : (n == 6 || n == 8 ? 1 : -1));
}
return (n - 18) / 8 + 3;
}
题目2
有两只动物先后交替吃草,每次吃4的k次幂(k为任意,可以为0,但吃草的数量不能超过草的总数量),给定一个数N,代表草的总数,谁先吃到最后一口把草吃完则获胜,每一次都要吃一定数量的草,不能不吃,假设两只动物都绝顶聪明,返回先吃的动物获胜还是后吃的动物获胜。(当草的数量为0时,后吃的动物获胜)
普通解法
思路:N属于0~4就直接输出,否则就调用递归,我先手从拿一个开始,每次都调用递归看看我会不会赢,我赢了就返回先手,我没赢就继续拿4个,还没赢就拿16个,依次往下直到我拿的草数要大于N了,返回后手赢。
string winner(int n)
{
//0 1 2 3 4
//后 先 后 先 先
if (n < 5)
{
return (n == 0 || n == 2) ? "后手" : "先手";
}
int base = 1;
while (base <= n)
{
if (winner(n - base) == "后手") //后手的后手就是我的先手,我赢了就返回先手,否则继续往下试
{
return "先手";
}
if (base > n / 4)
{
break;
}
base *= 4;
}
return "后手";
}
打表法
输出输入参数从0到49的结果,看规律

输出结果以后先后先先的顺序循环
//打表法代码
string winner2(int n)
{
if (n % 5 == 0 || n % 5 == 2)
{
return "后手";
}
else
{
return "先手";
}
}
预处理数组
观察代码是否有频繁搜索等行为,如果有,看看能不能通过申请辅助数组提前拿到值来避免这种行为(空间换时间)
题目1
牛牛有一些排成一行的正方形。每个正方形已经被染成红色或者绿色。牛牛现在可以选择任意一个正方形然后用这两种颜色的任意一种进行染色,这个正方形的颜色将会被覆盖。牛牛的目标是在完成染色之后,每个红色R都比每个绿色G距离最左侧近。牛牛想知道他最少需要涂染几个正方形。
如样例所示: s = RGRGR。我们涂染之后变成RRRGG满足要求了,涂染的个数为2,没有比这个更好的涂染方案。
思路1
先把整个字符串看成都是右侧,看一共有几个R,全染成G,记录染色个数。然后把s[0]看成左侧,剩下的看成右侧,看左侧有几个G,全染成R,看右侧有几个R,全染成G,记录染色的个数。然后是s[0]~s[1]看成左侧,剩下的看成右侧,跟前面一样,记录染色的个数,之后左侧范围依次扩大,右侧范围依次缩小,直到全都看成左侧,所记录的染色个数最少的就是正确答案。
int minPaints(string s)
{
if (s.size() == 0)
{
return 0;
}
int min = INT_MAX;
int paints = 0;
for (int i = 0; i <= s.size(); i++)
{
paints = 0;
for (int j = 0; j < i; j++)
{
if (s[j] == 'G')
{
paints++;
}
}
for (int k = i; k < s.size(); k++)
{
if (s[k] == 'R')
{
paints++;
}
}
min = min > paints ? paints : min;
}
return min;
}
思路2
上面的代码时间复杂度为O(N2),就是因为每到一个位置,都要遍历一遍找R或G,这种遍历行为有必要吗?可不可以提前申请辅助数组,把需要的信息都统计好,然后直接拿数据呢。我们提前申请两个辅助数组,一个数组统计每个位置上左侧(包括自己)G的数量,另一个数组统计每个位置上右侧(包括自己)R的数量,遍历两遍统计,时间复杂度O(N),主流程的遍历直接拿数据,时间复杂度从O(N2)变成O(N),整体的时间复杂度就变成了O(N)
//优化后代码
int minPaints2(string s)
{
if (s.size() == 0)
{
return 0;
}
int min = INT_MAX;
vector<int> leftG(s.size());
leftG[0] = s[0] == 'G' ? 1 : 0;
vector<int> rightR(s.size());
rightR[s.size() - 1] = s[s.size() - 1] == 'R' ? 1 : 0;
for (int i = 1; i < s.size(); i++)
{
leftG[i] = s[i] == 'G' ? 1 + leftG[i - 1] : leftG[i - 1];
}
for (int i = s.size() - 2; i >= 0; i--)
{
rightR[i] = s[i] == 'R' ? 1 + rightR[i + 1] : rightR[i + 1];
}
for (int i = 0; i <= s.size(); i++) //从i开始(包括i)往右是右侧区域
{
if (i == 0) //当左侧区域长度为0时,只看右侧有多少个R
{
min = min > rightR[i] ? rightR[i] : min;
}
else if (i == s.size()) //当右侧区域长度为0时,只看左侧有多少个G
{
min = min > leftG[i - 1] ? leftG[i - 1] : min;
}
else
{
int paints = s[i] == 'G' ? leftG[i] + rightR[i] - 1 : leftG[i] + rightR[i]; //如果当前位置是G,会重复计算,所以减去1
min = min > paints ? paints : min;
}
}
return min;
}
题目2
给定一个N*N的矩阵matrix,只有0和1两种值,返回边框全是1的最大正方形的边长长度。
例如:
01111
01001
01001
01111
01011
其中边框全是1的最大正方形的大小为4 * 4,所以返回4。
思路1
遍历矩阵中每个位置,当前位置当作正方形的左上角,在不越界的情况下枚举正方形的边长,再检查四条边是不是都是1。
int maxSquare(vector<vector<int>> matrix)
{
if (matrix.size() == 0 || matrix[0].size() == 0)
{
return 0;
}
int row = matrix.size();
int col = matrix[0].size();
int max = 0; //记录全局最大边长
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
int maxLength = 0;
for (int k = 1; k <= min(row - i, col - j); k++)
{
maxLength = 0; //记录(i,j)位置正方形的最大边长
int checkTimes = 0; //统计检查的次数,如果每个位置都是1,则检查的次数等于周长4k
for (int n = j; n < j + k; n++)
{
if (matrix[i][n] != 1)
{
break;
}
checkTimes++;
}
if (checkTimes < k) //如果上面是从break跳出来的,则直接进行下一条边的枚举
{
continue;
}
for (int n = i; n < i + k; n++)
{
if (matrix[n][j + k - 1] != 1)
{
break;
}
checkTimes++;
}
if (checkTimes < 2 * k) //如果上面是从break跳出来的,则直接进行下一条边的枚举
{
continue;
}
for (int n = i; n < i + k; n++)
{
if (matrix[n][j] != 1)
{
break;
}
checkTimes++;
}
if (checkTimes < 3 * k) //如果上面是从break跳出来的,则直接进行下一条边的枚举
{
continue;
}
for (int n = j; n < j + k; n++)
{
if (matrix[i + k - 1][n] != 1)
{
break;
}
checkTimes++;
}
if (checkTimes == 4 * k) //每个位置都是1
{
maxLength = k;
}
}
max = maxLength > max ? maxLength : max; //更新全局最大边长
}
}
return max;
}
优化思路
上面的代码四层for循环嵌套,时间复杂度接近O(N4),最内部的循环是检查四条边是否都是1,能不能申请辅助空间省去循环检查的步骤?答案是能。首先申请两个大小与matrix一样的二维数组,一个二维数组储存每个位置从自己出发(包括自己)往右有多少个连续的1,另一个数组存储每个位置从自己出发(包括自己)往下有多少个连续的1,这样,当到达一个位置的时候,看它右边是否有大于等于k的1,下边是否有大于等于k的1,和它右边第k-1位置下方有没有大于等于k的1,以及它下方k-1位置的右边有没有大于等于k的1,把遍历行为变成直接拿值的行为,因为两个二维数组的填写的时间复杂度是O(N2),所以整体的时间复杂度变为O(N3)。
int maxSquare2(vector<vector<int>> matrix)
{
if (matrix.size() == 0 || matrix[0].size() == 0)
{
return 0;
}
int row = matrix.size();
int col = matrix[0].size();
int max = 0;
vector<vector<int>> rightOne(row, vector<int>(col));
vector<vector<int>> belowOne(row, vector<int>(col));
for (int i = 0; i < row; i++)
{
for (int j = col - 1; j >= 0; j--)
{
if (j == col - 1)
{
rightOne[i][j] = matrix[i][j] == 1 ? 1 : 0;
}
else
{
rightOne[i][j] = matrix[i][j] == 1 ? 1 + rightOne[i][j + 1] : 0;
}
}
}
for (int i = row - 1; i >= 0; i--)
{
for (int j = 0; j < col; j++)
{
if (i == row - 1)
{
belowOne[i][j] = matrix[i][j] == 1 ? 1 : 0;
}
else
{
belowOne[i][j] = matrix[i][j] == 1 ? 1 + belowOne[i + 1][j] : 0;
}
}
}
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
int maxLength = 0;
for (int k = 1; k <= min(row - i, col - j); k++)
{
maxLength = 0;
if (rightOne[i][j] < k || belowOne[i][j] < k)
{
continue; //不能是break,如果是break会直接退出枚举边长的循环,导致(i,j)位置的边长情况没有枚举完
}
if (rightOne[i + k - 1][j] < k || belowOne[i][j + k - 1] < k)
{
continue;
}
maxLength = k;
}
max = maxLength > max ? maxLength : max;
}
}
return max;
}
补充题目
题目1
给定一个函数f,可以1 ~ 5的数字等概率返回一个。请加工出1 ~ 7的数字等概率返回一个的函数g。
思路
用二进制去拼,f返回1或2就代表0,返回2或4就代表1,返回5就继续再让它重新返回1~4之间的数字,这样做成一个等概率返回0~1的01发生器。3个二进制位可以等概率返回0 ~ 7,那么怎么等概率返回1 ~ 7呢。先让01发生器生成随机生成0~6,如果生成了7就重新做。
int generate01();
int randomGenerateOneToSeven()
{
int res = 0;
do
{
res = (generate01() << 2) + (generate01() << 1) + generate01();
} while (res == 7);
return res + 1;
}
int generate01()
{
int res = 0;
do
{
res = f();
} while (res == 5);
return res < 3 ? 0 : 1;
}
题目2
给定一个函数f,可以a ~ b的数字等概率返回一个。请加工出c ~ d的数字等概率返回一个的函数g。
思路
把f加工成01发生器,一半数字返回1,一半数字返回0,如果是奇数个还多于一个那就遇到这个数字就重新生成。然后用二进制等概率生成0~c-d的数(生成多余的数就循环重新生成),最后加上c就可以了
题目3
给定一个函数f,以p概率返回0,以1-p概率返回1。请加工出等概率返回0和1的函数g
思路
生成00的概率是p * p,生成11的概率是(1-p) * (1-p),而生成01和10的概率都是(1-p) * p,所以当生成01时返回0,生成10时返回1,生成00或11时循环重新生成直到生成01或10。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号