算法学习(27):从暴力递归到动态规划(下)
从暴力递归到动态规划
算法学习(16)中的纸牌问题改成动态规划
给定一个整型数组arr,代表数值不同的纸牌排成一条线,纸牌上的数值代表分数。玩家A和玩家B依次拿走每张纸牌,规定玩家A先拿,玩家B后拿,但是每个玩家每次只能拿走最左或最右的纸牌,玩家A和玩家B都绝顶聪明。请返回最后获胜者的分数。
(记忆化搜索很容易就能改出,所以省略了,后面的题都是这样)假设给定的数组是[3,100,4,50],则
-
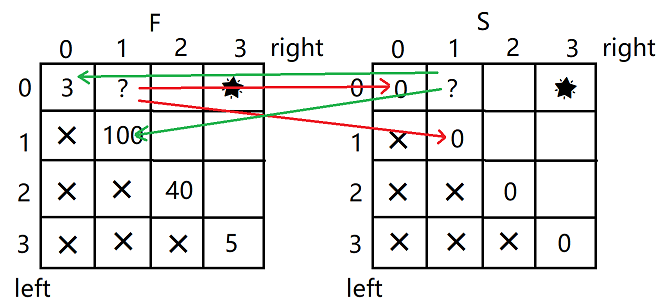
分析可变参数的变化范围,确定dp表的维度和大小。两个可变参数,范围都是0~arr.size()-1,所以维度是2,大小是4x4的二维表。这次是两个递归函数,一个先手一个后手,所以是两张表
![]()
-
标出要计算的目标位置。
![]()
-
根据base case填写表中已经知道的数据。F函数的base case是left=right时返回这个位置的数值,S函数的base case是left=right时返回0,又因为left不能大于right,所以两个表格左下角都是×
![]()
-
根据递归推出表中格子之间的依赖关系。根据递归函数可知,F表格的值等于,它的left下标在arr中对应的值加上它在S表格中相同位置下边格子的值,与它的right下标在arr中对应的值加上它在S表格中相同位置左边格子的值,两者之间较大的值。S表格的值则是等于它在F表格中相同位置下边格子、左边格子的值之间较小的值。
![]()
-
确定表中数据的依次计算的顺序。顺序有多种,这里采用沿着对角线从左上角到右下角填,F和S表交叉填写,填完一条斜线再填下一条
这一题是一种新的尝试方法:范围尝试,是两个表的形式,采用搭积木的方式决定谁先求谁后求
代码:
int maxScoreDP(vector<int> arr)
{
int length = arr.size();
vector<vector<int>> F(length, vector<int>(length));
vector<vector<int>> S(length, vector<int>(length));
for (int i = 0; i < length; i++)
{
F[i][i] = arr[i];
}
int row = 0;
int col = 1;
while (col < length)
{
int i = row;
int j = col;
while (i < length && j < length)
{
F[i][j] = max(arr[i] + S[i + 1][j], arr[j] + S[i][j - 1]);
S[i][j] = min(F[i + 1][j], F[i][j - 1]);
j++;
i++;
}
col++;
}
return max(F[0][length - 1], S[0][length - 1]);
}
象棋问题(三维表)
有一个10*9的棋盘,一个马,它的初始位置是(0,0),给定一个目标位置(a,b)和步数K,马必须走K步到(a,b),返回有多少种走法
暴力递归
比较好理解的思路是反过来,把马看作是从(a,b)到(0,0),每次走八个方向,调用八个方向的递归,越界就返回0,步数走完且到了(0,0)就返回1。
int process(int x, int y, int rest);
int knight(int a, int b, int k)
{
return process(a, b, k);
}
int process(int x, int y, int rest) //x,y代表坐标,rest代表还有多少步要走
{
if (rest == 0)
{
return (x == 0 && y == 0) ? 1 : 0; //步数走完,且到了(0,0)
}
if (x > 8 || x < 0 || y > 9 || y < 0) //越界,前面所作的选择是错的
{
return 0;
}
return process(x + 1, y + 2, rest - 1)
+ process(x + 2, y + 1, rest - 1)
+ process(x + 2, y - 1, rest - 1)
+ process(x + 1, y - 2, rest - 1)
+ process(x - 1, y - 2, rest - 1)
+ process(x - 2, y - 1, rest - 1)
+ process(x - 2, y + 1, rest - 1)
+ process(x - 1, y + 2, rest - 1); //调用八个方向的递归,把它们的方法数加起来并返回
}
动态规划
-
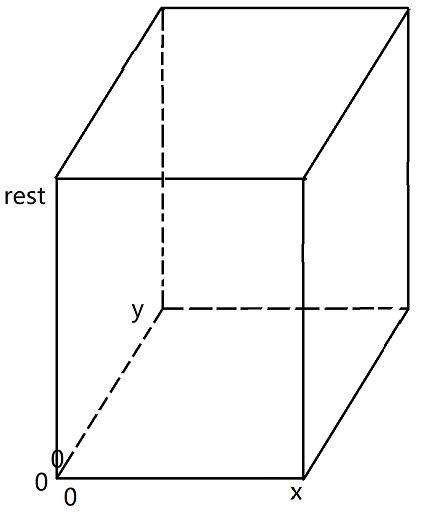
分析可变参数的变化范围,确定dp表的维度和大小。三个可变参数,x的范围是08,y的范围是09,rest的范围是0~k。
![]()
-
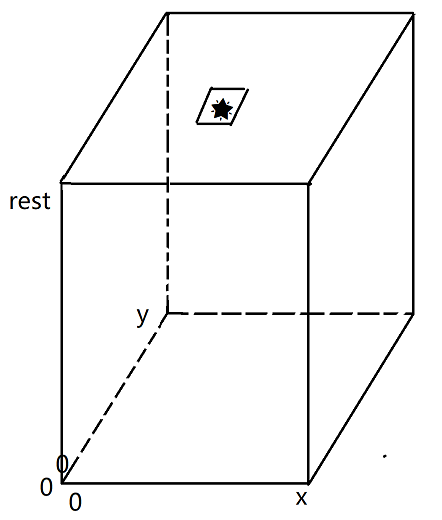
标出要计算的目标位置。需要计算的目标位置为最上层的某个位置
![]()
-
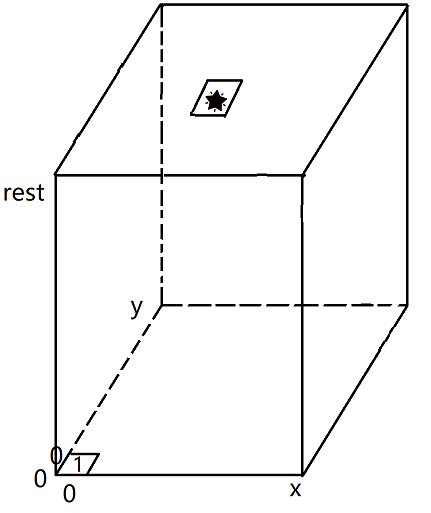
根据base case填写表中已经知道的数据。最下层即第0层除了(0,0)点是1外,其他点都是0
![]()
-
根据递归推出表中格子之间的依赖关系。根据递归可得,上一层需要自己在下一层对应位置的八个方向上的值的和,越界的方向就为0
-
确定表中数据的依次计算的顺序。从下到上填
int knight(int a, int b, int k)
{
vector<vector<vector<int>>> dp(9, vector<vector<int>>(10, vector<int>(k + 1)));
dp[0][0][0] = 1;
for (int h = 1; h < k + 1; h++)
{
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 10; j++)
{
dp[i][j][h] += getValue(dp, i + 1, j + 2, h - 1);
dp[i][j][h] += getValue(dp, i + 2, j + 1, h - 1);
dp[i][j][h] += getValue(dp, i + 2, j - 1, h - 1);
dp[i][j][h] += getValue(dp, i + 1, j - 2, h - 1);
dp[i][j][h] += getValue(dp, i - 1, j - 2, h - 1);
dp[i][j][h] += getValue(dp, i - 2, j - 1, h - 1);
dp[i][j][h] += getValue(dp, i - 2, j + 1, h - 1);
dp[i][j][h] += getValue(dp, i - 1, j + 2, h - 1);
}
}
}
return dp[a][b][k];
}
bob生存问题(三维表)
给定两个参数N和M,在N*M的地图上有一个人bob,它每次等概率上下左右移动一步,一旦走到地图范围外,bob就会死亡,给定一个参数K,代表bob必须走K步,求bob走完k步之后还活着的概率。
暴力递归
首先算出存活的方法数,在当前位置,出界返回0,rest归零且没出界返回1,上下左右每个位置调用一次递归并且相加,再返回。在主函数中最后把方法数除以所有走的可能性4k再返回即可(与递归函数process返回值res除以4结果一样)。
int process(int N, int M, int i, int j, int rest);
double bobProbability(int N, int M, int i, int j, int K)
{
if (N <= 0 || M <= 0 || i < 0 || j < 0 || K < 0)
{
return 0;
}
double ways = process(N, M, i, j, K);
return ways / pow(4, K);
}
int process(int N, int M, int i, int j, int rest)
{
if (i < 0 || i > N - 1 || j < 0 || j > M - 1)
{
return 0;
}
if (rest == 0)
{
return 1;
}
int res = 0;
res += process(N, M, i - 1, j, rest - 1);
res += process(N, M, i + 1, j, rest - 1);
res += process(N, M, i, j + 1, rest - 1);
res += process(N, M, i, j - 1, rest - 1);
return res;
}
动态规划
- 分析可变参数的变化范围,确定dp表的维度和大小。三个可变参数,i的取值范围是0N-1,j的取值范围是0M-1,rest的取值范围是0~k。
![]()
- 标出要计算的目标位置。
![]()
- 根据base case填写表中已经知道的数据。第0层的值都是1
![]()
- 根据递归推出表中格子之间的依赖关系。根据递归可得,上一层需要自己在下一层对应位置的上下左右四个方向上的值的和,越界的方向就为0
- 确定表中数据的依次计算的顺序。从下到上填
int getValue(vector<vector<vector<double>>>& dp, int N, int M, int i, int j, int K);
double bobProbability(int N, int M, int i, int j, int K)
{
vector<vector<vector<double>>> dp(N, vector<vector<double>>(M, vector<double>(K + 1)));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
dp[i][j][0] = 1.0;
}
}
for (int h = 1; h < K + 1; h++)
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
dp[i][j][h] += getValue(dp, N, M, i + 1, j, h - 1);
dp[i][j][h] += getValue(dp, N, M, i - 1, j, h - 1);
dp[i][j][h] += getValue(dp, N, M, i, j - 1, h - 1);
dp[i][j][h] += getValue(dp, N, M, i, j + 1, h - 1);
}
}
}
return dp[i][j][K] / pow(4, K);
}
int getValue(vector<vector<vector<double>>>& dp, int N, int M, int i, int j, int K)
{
if (i < 0 || i > N - 1 || j < 0 || j > M - 1)
{
return 0;
}
return dp[i][j][K];
}
零钱兑换(斜率优化)
给你一个整数数组coins,表示不同面额的硬币;以及一个整数aim,表示总金额。
计算并返回可以凑成总金额的方法数。如果没有任何一种硬币组合能组成总金额,返回-1 。
你可以认为每种硬币的数量是无限的。
暴力递归
经典的从左到右试,当前index位置的硬币拿0~aim/coins[index]枚,依次调用递归,最后全部相加再返回。base case是越界并且剩余钱数为0。
int minCoins(vector<int> coins, int aim)
{
if (coins.size() > 0 && aim >= 0)
{
return process(coins, 0, aim);
}
return 0;
}
int process(vector<int> coins, int index, int rest)
{
if (index == coins.size())
{
return rest == 0 ? 1 : 0;
}
int ways = 0;
for (int nums = 0; nums * coins[index] <= rest; nums++)
{
ways += process(coins, index + 1, rest - coins[index] * nums);
}
return ways;
}
动态规划
-
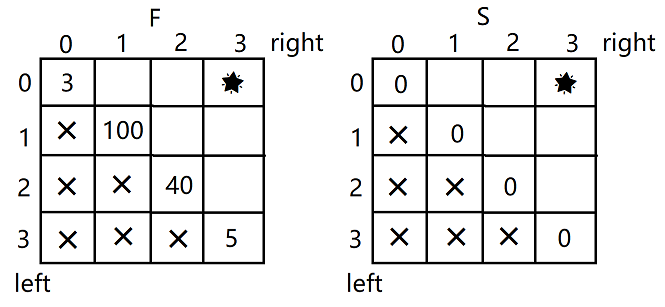
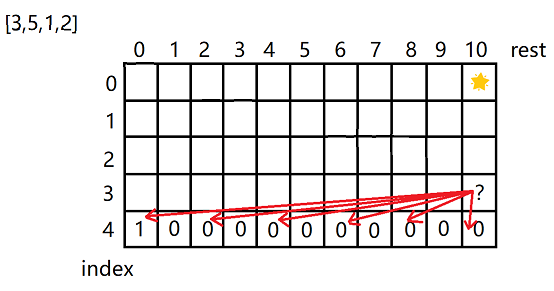
分析可变参数的变化范围,确定dp表的维度和大小。可变参数为两个,index的取值范围为0 ~ coins.size(),rest的取值范围为0 ~ aim。假设coins为[3,5,1,2],aim=10,则
![]()
-
标出要计算的目标位置。
![]()
-
根据base case填写表中已经知道的数据。
![]()
-
根据递归推出表中格子之间的依赖关系。根据递归,当前index位置的值等于下一行rest-arr[index]*(0,1,2,3.......)位置(不越界)的值的和。
![]()
-
确定表中数据的依次计算的顺序。从下到上,从左到右。
代码:
int minCoins(vector<int> coins, int aim)
{
int size = coins.size();
vector<vector<int>> dp(size + 1, vector<int>(aim + 1));
dp[size][0] = 1;
for(int i = size - 1; i >= 0; i--)
{
for (int j = 0; j <= aim; j++)
{
for (int nums = 0; nums * coins[i] <= j; nums++)
{
dp[i][j] += dp[i + 1][j - coins[i] * nums];
}
}
}
return dp[0][aim];
}
斜率优化
在上面的动态规划中,三层for循环的最内层存在枚举行为
for (int nums = 0; nums * coins[i] <= j; nums++)
{
dp[i][j] += dp[i + 1][j - coins[i] * nums];
}
如果coins[i]=1,那么就会把下一行所有格子的数都加起来,那么外层的时间复杂度O(N* aim),枚举的时间复杂度O(aim),他们造成的结果是整个算法的时间复杂度为O(N*aim2)。那么真的有必要枚举吗?这一题中其实是不需要的,如下图
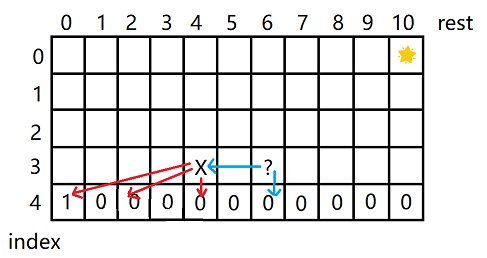
我们要求?位置的值,注意看X位置,即?位置向左偏移一个coin[i]的dp[i][j - coins[i]]位置,由于X位置与?位置处于同一行,所以每次的偏移量一样,所以?位置的值就等于X位置的值加上?位置下面格子的值。由于是从左到右计算的,所以X位置的值已经事先知道,这样就可以把枚举行为变为直接拿值的行为,把时间复杂度从O(aim)降为O(1)。
优化后代码
int minCoins(vector<int> coins, int aim)
{
int size = coins.size();
vector<vector<int>> dp(size + 1, vector<int>(aim + 1));
dp[size][0] = 1;
for (int i = size - 1; i >= 0; i--)
{
for (int j = 0; j <= aim; j++)
{
dp[i][j] = j - coins[i] < 0 ? dp[i + 1][j] : dp[i + 1][j] + dp[i][j - coins[i]];
}
}
return dp[0][aim];
}
从暴力递归到动态规划总结
- 优化流程:暴力递归(左右尝试、范围尝试)->记忆化搜索->严格表结构的dp->更加精致的严格表结构dp
- 尝试方法优劣的评估标准
(1)每个可变参数的维度越低越好。最好是int类型的变量,即0维变量,如果是一个数组,则列起来太多太复杂。
(2)可变参数的个数越少越好。多一个参数,dp表就多一个维度,所以越少越好。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号