算法学习(26):从暴力递归到动态规划(上)
从暴力递归到动态规划
优化顺序:暴力递归->记忆化搜索->严格(多维)表结构(dp)
记忆化搜索不考虑依赖关系,严格(多维)表结构需要规定每一个状态的依赖顺序。在某些问题上记忆化搜索和严格(多维)表结构拥有相同的时间复杂度,但是严格(多维)表结构可以进一步优化,当你把每一个位置的依赖关系都整理出来并非常熟悉有可能进入到下一步优化,即更加精致的严格表结构动态规划,到这一步优化就结束了。
无后效性的尝试
无后效性的尝试:可变参数确定,不管谁调用的,返回值都是一样的,之前的决定不影响你现在的结果
无后效性尝试非常适合改动态规划,面试场合中遇到的动态规划都可以改成无后效性尝试,因为面试官想要考察你动态规划的能力
机器人运动问题(阿里面试原题)
给定一个参数N,代表有1~N个位置,N > 1;一个参数S,代表机器人的初始位置;一个参数E,代表机器人的目标位置;一个参数K,代表机器人必须走K步。机器人的目标是从S位置走到E位置,中间必须走K步,当机器人走到1位置时,只能往右走到2位置;走到N位置时,只能往左走到N-1位置;其他位置都可以左右两边走
返回一共有多少种走法
第一步:写出暴力递归
思路:当前位置是1时,往右走,当前位置是N时,往左走,其他位置可以往左走也可以往右走,base case是当步数为0时,我当前位置在E,返回1,代表这种决策是正确的,如果没在E,返回0。
int process(int N, int E, int rest, int cur);
int walkWays(int N, int S, int E, int K)
{
return process(N, E, K, S);
}
int process(int N, int E, int rest, int cur) //cur代表当前位置,rest代表还剩多少步
{
if (rest == 0)
{
return cur == E ? 1 : 0;
}
if (cur == 1)
{
return process(N, E, rest - 1, cur + 1); //当前位置是1时,往右走
}
if (cur == N)
{
return process(N, E, rest - 1, cur - 1); //当前位置是N时,往左走
}
return process(N, E, rest - 1, cur - 1) + process(N, E, rest + 1, cur + 1); //往左走的正确走法数加上往右走的正确走法数
}
第二步:根据可变参数数量添加多维表,变成记忆化搜索
什么叫记忆化搜索
当你把暴力递归的递归树展开的时候会发现,有一些重复出现的调用,例如上面的process函数中rest参数和cur参数一样的时候,如果你的尝试是无后效性的尝试,那么当它被不同的上层调用时的结果是一样的,那么这些重复的调用就会很多余,因为当你第一次调用计算出这个函数的返回值时,以后每一次调用这个函数都不应该再去算一遍,这时候就需要记忆化搜索。记忆化搜索就是加一个多维数组dp作为缓存,有几个可变参数就是几维,它的大小是根据可变参数的取值范围决定的(最好比取值范围的最大值大1,保证空间足够),dp的初始值是base case中不出现的值。递归时带着dp去进行,首先判断当前函数对应的dp中的位置的值是否是初始化的值,如果不是,那就直接返回数组中的值,这样就不需要计算。如果是初始化的值,则下面计算完在返回的时候先更新dp数组中的值,再返回。
修改完后的记忆化搜索
int process(vector<vector<int>>& dp, int N, int E, int rest, int cur);
int walkWays(int N, int S, int E, int K)
{
vector<vector<int>> dp(K + 1, vector<int>(N + 1));
for (int i = 0; i < K + 1; i++) //初始化,把所有格子的值都设置为-1
{
for (int j = 0; j < N + 1; j++)
{
dp[i][j] = -1;
}
}
return process(dp, N, E, K, S);
}
int process(vector<vector<int>>& dp, int N, int E, int rest, int cur) //cur代表当前位置,rest代表还剩多少步
{
if (dp[rest][cur] != -1) //当前位置在dp里的值不是初始值-1时,直接返回里面的值
{
return dp[rest][cur];
}
if (rest == 0)
{
dp[rest][cur] = cur == E ? 1 : 0;
return dp[rest][cur];
}
if (cur == 1)
{
dp[rest][cur] = process(dp, N, E, rest - 1, cur + 1); //当前位置是1时,往右走
}
else if (cur == N)
{
dp[rest][cur] = process(dp, N, E, rest - 1, cur - 1); //当前位置是N时,往左走
}
else
{
dp[rest][cur] = process(dp, N, E, rest - 1, cur + 1) + process(dp, N, E, rest - 1, cur - 1);
}
return dp[rest][cur]; //往左走的正确走法数加上往右走的正确走法数
}
记忆化搜索的时间复杂度
二维表是K * N的位置需要填,那么时间复杂度就是O(K * N)
第三步:改成动态规划
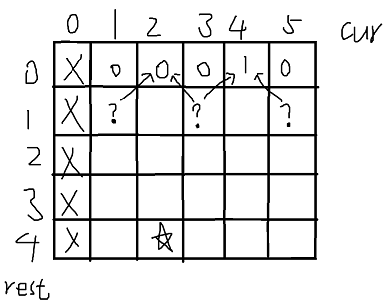
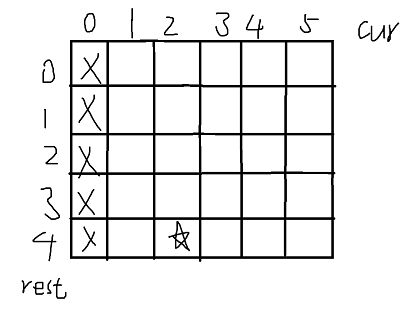
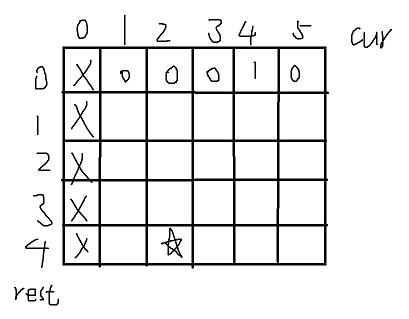
- 首先根据缓存表dp画出图,假设N=5,K=4,起始位置是2,目标位置E是4,则(由于不能走到0位置,所以第一列画❎。目标是得到process(4, 2)的值,即从2位置开始走四步,所以这个位置画⭐)
![]()
- 根据base case把图中可以直接得到答案的格子填上答案,当rest=0时,cur=4的位置为1,其他为0。
![]()
- 根据递归函数确定格子的依赖关系,一步一步推出⭐的值。
如何确定格子之间的依赖关系?看递归
if (cur == 1)
{
dp[rest][cur] = process(dp, N, E, rest - 1, cur + 1); //当前位置是1时,往右走
}
else if (cur == N)
{
dp[rest][cur] = process(dp, N, E, rest - 1, cur - 1); //当前位置是N时,往左走
}
else
{
dp[rest][cur] = process(dp, N, E, rest - 1, cur + 1) + process(dp, N, E, rest - 1, cur - 1);
}
当cur来到1位置,它依赖于(rest-1, cur+1)位置,即它表格右上角的值;当cur来到N位置,它依赖于(rest-1, cur-1)位置,即它表格左上角的值;当cur处于一般位置,依赖于(rest-1, cur+1)、(rest-1, cur-1)位置的和,即它表格左上角和右上角值的和。这样就确定了表格填写的步骤是从上到下从左到右,一步一步把表格内的值填完,最后返回(4,2)的值。
C++代码:
int walkWaysDP(int N, int S, int E, int K)
{
vector<vector<int>> dp(K + 1, vector<int>(N + 1)); //初始化dp表
dp[0][E] = 1; //根据base case把可以直接得到答案的格子填上,由于C++vector容器初始化之后是以0填充的,所以只要把第一行的dp[0][E]填上1就行了。
for (int i = 1; i < K + 1; i++)
{
for (int j = 1; j < N + 1; j++)
{
if (j == 1)
{
dp[i][j] = dp[i - 1][j + 1]; //当cur来到1位置,依赖右上角的值
}
else if (j == N)
{
dp[i][j] = dp[i - 1][j - 1]; //当cur来到N位置,依赖左上角的值
}
else
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1]; //当cur处于一般位置,它左上角和右上角值的和
}
}
}
return dp[K][S]; //返回结果
}
拿硬币题
有一个正整数数组,里面的每个数字代表面值为这个数字的一枚硬币,给定一个正整数aim,返回最少的能组成aim的硬币数。
第一步:暴力递归
01背包问题,要或者不要,从左往右试
int process(vector<int> arr, int index, int rest);
int minCoins(vector<int> arr, int aim)
{
int res = process(arr, 0, aim);
return res > arr.size() ? -1 : res; //判断结果是否大于数组的长度,即没有任何方法凑到aim,大于则返回-1,否则返回自身
}
int process(vector<int> arr, int index, int rest) //index代表从arr[index]到后面(包括arr[index])都可以任意选择,rest代表还剩多少钱需要拿
{
if (rest < 0) //拿的钱数超了,返回数组长度+1代表这种方法不行
{
return arr.size() + 1;
}
if (rest = 0) //钱数正好,返回0代表不拿了
{
return 0;
}
if (index = arr.size()) //钱数不够还越界,返回数组长度+1代表这种方法不行
{
return arr.size() + 1;
}
//当前硬币不拿 //当前硬币拿
return min(process(arr, index + 1, rest), 1 + process(arr, index + 1, rest - arr[index])); //取拿和不拿的最小值
}
第二步:根据可变参数数量添加多维表,变成记忆化搜索
可变参数是两个,所以dp是二维表,index的取值范围是0 ~ arr.size()-1,rest的取值范围是0 ~ aim
int process2(vector<int> arr, int index, int rest, vector<vector<int>> &dp);
int minCoins2(vector<int> arr, int aim)
{
vector<vector<int>> dp(arr.size() + 1, vector<int>(aim + 1));
for (int i = 0; i < arr.size() + 1; i++)
{
for (int j = 0; j < aim + 1; j++)
{
dp[i][j] = -1;
}
}
int res = process(arr, 0, aim);
return res > arr.size() ? -1 : res;
}
int process2(vector<int> arr, int index, int rest, vector<vector<int>>& dp)
{
if (dp[index][rest] != -1)
{
return dp[index][rest];
}
if (rest < 0)
{
return arr.size() + 1;
}
if (rest == 0)
{
dp[index][rest] = 0;
}
else if (index = arr.size())
{
dp[index][rest] = arr.size() + 1;
}
else
{
dp[index][rest] = min(process(arr, index + 1, rest), 1 + process(arr, index + 1, rest - arr[index]));
}
return dp[index][rest];
}
第三步:改成动态规划
假设给定的数组是[2,3,5,7,2],aim=10,根据base case填好已经知道的格子,用⭐标记目标位置,则
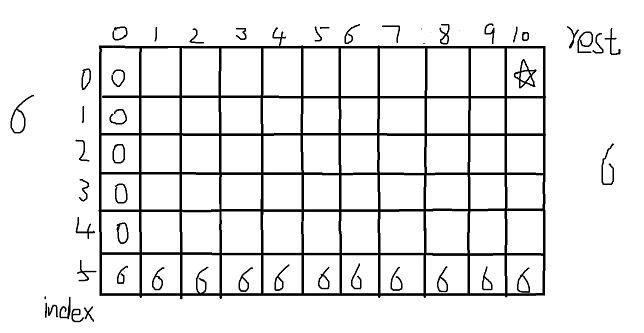
根据递归可以看出当前位置依赖于(index+1,rest)和(index+1,rest-arr[index]),即它正下方的格子和左下方当前rest-arr[index]位置格子之间较小的那个(不能越界,越界的值为arr.size()+1)。也确定了表格从下往上从左往右填写。
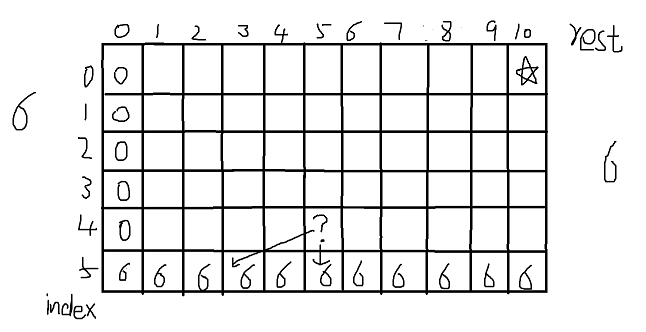
代码如下:
int minCoinsDP(vector<int> arr, int aim)
{
int length = arr.size();
vector<vector<int>> dp(length + 1, vector<int>(aim + 1));
for (int i = 0; i < length + 1; i++)
{
dp[i][0] = 0;
}
for (int i = 0; i < aim + 1; i++)
{
dp[length][i] = length + 1;
}
for (int i = length - 1; i >= 0; i--)
{
for (int j = 1; j < aim + 1; j++)
{
if (j - arr[j] >= 0)
{
dp[i][j] = min(dp[i + 1][j], dp[i + 1][j - arr[j]]);
}
else
{
dp[i][j] = dp[i + 1][j];
}
}
}
return dp[0][aim] > (length + 1) ? -1 : dp[0][aim];
}
暴力递归到动态规划步骤总结
- 通过尝试写出暴力递归
- 加缓存变成记忆化搜索
- 动态规划
(1)分析可变参数的变化范围,确定dp表的维度和大小
(2)标出要计算的目标位置
(3)根据base case填写表中已经知道的数据
(4)根据递归推出表中格子之间的依赖关系
(5)确定表中数据的依次计算的顺序



 浙公网安备 33010602011771号
浙公网安备 33010602011771号