算法学习（18）：并查集

并查集

岛问题

[题目]
一个矩阵中只有0和1两种值，每个位置都可以和自己的上、下、左、右四个位置相连，如
果有一片1连在一起，这个部分叫做一个岛，求一个矩阵中有多少个岛?
[举例]
001010
111010
100100
000000
这个矩阵中有三个岛

普通解法

遍历矩阵，每到一个位置判断是不是1，如果是统计岛数量的int类型变量result+1，然后调用感染函数将这个岛的所有1感染成2。感染函数是一个递归函数，base case是越不越界和是不是1，如果不是base case就把1改成2，然后下面分别上下左右递归一次感染函数

void infect(vector<vector<int>> &matrix, int i, int j, int m, int n);

int island(vector<vector<int>> matrix)
{
    if (matrix.size() == 0 || matrix[0].size() == 0)
    {
        return 0;
    }
    int res = 0;
    int m = matrix.size();
    int n = matrix[0].size();
    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (matrix[i][j] == 1)
            {
                res++;
                infect(matrix, i, j, m, n);
            }
        }
    }
    return res;
}

void infect(vector<vector<int>> &matrix, int i, int j, int m, int n)
{
    if (i < 0 || i >= m || j < 0 || j >= n || matrix[i][j] != 1)
    {
        return;
    }
    matrix[i][j] = 2;
    infect(matrix, i + 1, j, m, n);
    infect(matrix, i, j + 1, m, n);
    infect(matrix, i - 1, j, m, n);
    infect(matrix, i, j - 1, m, n);
}

如何设计一个并行算法解决这个问题（面试中如果遇到并行算法的问题，由于代码会很复杂，往往只需要讲清楚算法，不需要写代码）

这个问题在看完下面的并查集之后给出答案

并查集

什么是并查集

对于一个集合S={a1, a2, ..., an-1, an}，我们还可以对集合S进一步划分: S1,S2,...,Sm-1,Sm，我们希望能够快速确定S中的两两元素是否属于S的同一子集。
举个栗子，S={0，1, 2, 3, 4, 5, 6}，如果我们按照一定的规则对集合S进行划分，假设划分后为S1={1, 2, 4}，S2={3, 6}，S3={0, 5}，任意给定两个元素，我们如何确定它们是否属于同一子集？某些合并子集后，又如何确定两两关系？基于此类问题便出现了并查集这种数据结构。
并查集有两个基本操作：

isSameSet: 查找两个元素是否属于同一个集合
union：合并两个子集为一个新的集合

经典结构实现并查集的不足之处

链表实现并查集，union方法会很快，可以达到O(1)，但是isSameSet需要遍历链表，做不到O(1)
哈希表实现并查集isSameSet方法会很快，可以达到O(1)，但是union方法需要把一张表里的所有元素重新加到另一张表里去，做不到O(1)

isSameSet方法和union方法做到几乎都是O(1)的结构

向上指的图：
初始时每个元素自己外部包一层，有个指针指向自己。调用isSameSet方法时，两个元素都通过指针往上走，一直走到不能再往上所找到的点，叫做集合的代表元素，如果两个元素找到的集合代表元素相同，则两个元素属于同一个集合。调用union方法时，首先用isSameSet方法判定是否是同一个集合，如果不是，则两个元素向上走，找到各自集合的代表元素，之后比较两个集合元素个数的多少，少的那个集合的集合代表元素的指针指向多的那个集合的集合代表元素，这样就完成了union

路径压缩：并查集向上找集合代表元素过程的优化

如果isSameSet方法只做查找操作，那么由于union的频繁使用，链会越来越长，这样查找的效率就会越来越低。isSameSet方法在查找的过程中，每找到一个集合代表元素，就把发起查找的元素的指针重新指向它的集合代表元素，这样就可以做到扁平化，如果这个元素下次再发起查找，那么往上走一步就可以找到集合代表元素。

C++代码实现

class Element
{
public:
    Element(string value)
    {
        this->m_Value = value;
    }
public:
    string m_Value;
};

class UnionFindSet
{
public:
    UnionFindSet(list<string> str)   //初始化并查集的时候需要用户把所有的元素都传进来，这里采用了list的方式，也可以用其他方式
    {
        for (auto value : str)
        {
            Element *temp = new Element(value);
            elementMap.insert(make_pair(value, temp));
            fatherMap.insert(make_pair(temp, temp));       //初始时自己的父就是自己
            sizeMap.insert(make_pair(temp, 1));          //初始时每个元素都是自己集合的代表元素，每个集合元素个数都是1
        }
    }

    ~UnionFindSet()       //由于并查集内部自己在用户传入的元素外包了一层，即用new在堆区开辟了空间，等并查集调用自己的析构函数时需要释放这些空间
    {
        Element* temp = nullptr;
        for (auto element : elementMap)
        {
            temp = element.second;
            elementMap.erase(element.first);
            delete temp;
            temp = nullptr;
        }
    }

public:
    bool isSameSet(string str1, string str2)
    {
        if (elementMap.count(str1) != 0 && elementMap.count(str2) != 0)
        {
            return findHead(elementMap.at(str1)) == findHead(elementMap.at(str2));
        }
        return false;
    }

    void unionSet(string str1, string str2)
    {
        if (elementMap.count(str1) != 0 && elementMap.count(str2) != 0)
        {
            Element* small = nullptr;
            Element* big = nullptr;
            Element* head1 = findHead(elementMap.at(str1));
            Element* head2 = findHead(elementMap.at(str2));
            if (head1 != head2)
            {
                big = sizeMap.at(head1) > sizeMap.at(head2) ? head1 : head2;
                small = big == head1 ? head2 : head1;
                fatherMap.at(small) = big;
                sizeMap.at(big) += sizeMap.at(small);
                sizeMap.erase(small);
            }
        }
    }

private:
    Element* findHead(Element* element)
    {
        Element* temp = element;
        stack<Element*> path;
        while (temp != fatherMap.at(temp))
        {
            path.push(temp);
            element = fatherMap.at(temp);
        }
        while (!path.empty())
        {
            fatherMap.at(path.top()) = temp;
            path.pop();
        }
        return temp;
    }

private:
    unordered_map<string, Element*> elementMap;   //key代表用户传入的元素，value代表外面包了一层的元素
    unordered_map<Element*, Element*> fatherMap;   //key代表元素，value代表这个元素的父节点
    unordered_map<Element*, int> sizeMap;     //key代表一个集合的代表元素，value代表这个集合中有多少个元素
};

并查集的时间复杂度

数学证明太复杂，单说结论：假设样本有N个，findhead函数调用次数如果逼近或超过O(N)，单次平均调用findhead的时间复杂度为O(1)，所以整体的时间复杂度也是O(1)。

并行算法解决岛问题

假设这个岛很大，需要多个CPU去计算。如下图，把岛分割成左右两边用两个cpu去计算，先分别统计分割完后每个矩阵中岛的个数，和边界上的1是由谁感染（感染完是2，应该是统计2是由谁感染来的，图中用的是1，所以就描述1。且图中只分成了两份，只统计中间的边界，当分成很多份时，四个边界都统计）。从上到下第一条绿色线划出来的两个1分别是会由图中圈出的A和C两个1感染成2，第二条绿色线的1会由B和C感染，第三条绿色线的1也会由B和C感染。

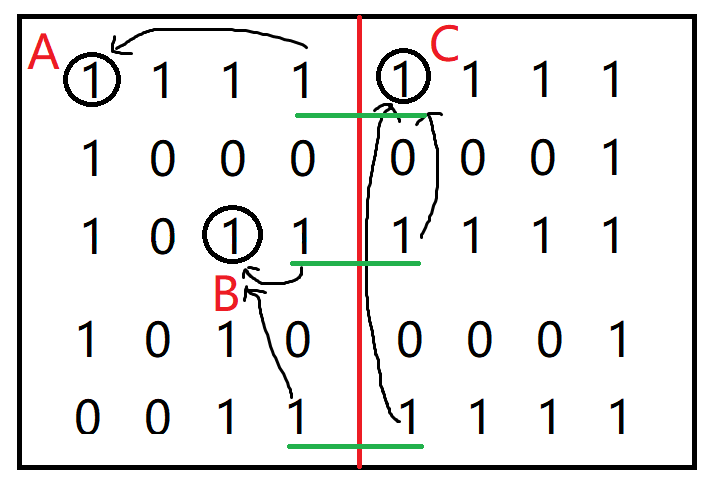
这时候就要用并查集了，先把要去重的两个矩阵的岛的个数相加，左边是2，右边是1，所以是3。然后把边界上的每对1各自的感染源全部放入并查集初始化，A、B、C分别在一个集合里，然后每对1分别看两个感染源是不是同一个。第一对的感染源是A和C，不是同一个集合，岛的总数量-1，变成2，把A和C所在的集合合并。看第二对1，感染源是B、C，不是同一个集合，岛的总数量-1，变成1，把B和C所在的集合合并。最后看第三对1，感染源是B、C，是同一个集合，岛的总数量不变。至此边界上所有对1都统计完了，这两个矩阵合并的岛的数量结果就是1。

posted @ 2022-07-31 10:48 小肉包i 阅读(51) 评论(0) 收藏举报

刷新页面返回顶部