算法学习(12):图
图
图的多种数据存储结构
邻接表
邻接矩阵
面对不同题目给出的图的存储结构不同的解题方法
先用自己熟悉的图的存储结构实现一遍算法算法,然后写一个接口,把题目给出的结构转化成自己熟悉的结构
比较好用的图的结构
下面的结构几乎可以兼顾所有题目的要求,实际刷题中可以用数组代替举例的图结构的哈希表(因为实际的题节点有限)
具体描述起来就是:首先一个图包含点集和边集。点集里面包含图里所有的点,每个点包含各自的出度、入度等属性;边集包含图中所有边,每个边包含各自的权值、从哪个点出发、指向哪个点的属性。
class Edge;
class Node
{
public:
Node() {};
Node(int value)
{
this->m_Value = value;
this->m_In = 0;
this->m_Out = 0;
}
public:
int m_Value; //点上的值,如果点是ABCD,则这一项为string类型
int m_In; //点的入度
int m_Out; //点的出度
vector<Node> m_Nexts; //该点发散出去的边直接相连的点。有向图中是从该点出去的边连接的点,无向图中就是与该点直接相连的点
vector<Edge> m_Edges; //属于该点的边。有向图中是从该点出去的边,无向图是和该点相连的边
};
class Edge
{
public:
Edge(int weight)
{
this->m_Weight = weight;
}
public:
int m_Weight; //边的权值
Node m_From; //该边从哪个点出发
Node m_To; //该边指向哪个点
//无向图中定义两条边 from和to相反
};
图的广度优先遍历
思路:利用队列实现,从源节点开始,依次按照广度进队列,然后弹出,每弹出一个点,把该节点所有没有进过队列的邻接点放入队列,直到队列变空
C++代码实现:
void BFS(Node node)
{
queue<Node> queue;
unordered_set<Node*> nodeSet; //辅助哈希表,用来储存已经进过队列的点
queue.push(node);
nodeSet.insert(&node);
while (!queue.empty())
{
Node cur = queue.front();
queue.pop();
printNode(cur);
for (auto next : cur.m_Nexts)
{
if (nodeSet.count(&next) == 0)
{
queue.push(next);
nodeSet.insert(&next);
}
}
}
}
图的深度优先遍历
思路:利用栈实现,从源节点开始,依次按照深度进栈,然后弹出,每弹出一个点,把该节点下一个没有进过栈的邻接点放入栈,直到栈变空
代码实现中要注意的点:在弹出节点后,如果这个节点后面还有节点,则把这个节点包括后面那个节点压回栈中去,然后跳出本次循环
C++代码实现:
void DFS(Node node)
{
//if (node == NULL)
//{
// return;
//}
stack<Node> stack;
unordered_set<Node*> nodeSet; //辅助哈希表,用来储存已经进过队列的点
stack.push(node);
nodeSet.insert(&node);
while (!stack.empty())
{
Node cur = stack.top();
stack.pop();
for (auto next : cur.m_Nexts)
{
if (nodeSet.count(&next) == 0)
{
stack.push(cur);
stack.push(next);
nodeSet.insert(&next);
printNode(next);
break;
}
}
}
}
拓扑排序
思路:找到入度为0的点,打印,然后把这个点与它产生的影响删掉(从这个点出发的边删掉、这些边指向的点的入度减一),然后再找下一个入度为0的点,循环下去,直到没有点了。
C++代码实现:
vector<Node> topologicalSort(Graph graph)
{
unordered_map<Node*, int> inMap; //key代表图中的点,value代表该点的入度
queue<Node> zeroInQueue; //入度为0的点进队列
for (auto node : graph.m_Nodes())
{
inMap.insert(make_pair(&node.second, node.second.m_In));
if (node.second.m_In == 0)
{
zeroInQueue.push(node);
}
}
vector<Node> result;
while (!zeroInQueue.isEmpty())
{
Node cur = zeroInQueue.front();
zeroInQueue.pop();
result.push_back(cur);
for (auto next : cur.m_Nexts)
{
inMap.at(&next)--;
if (inMap.at(&next) == 0)
{
zeroInQueue.push(next);
}
}
}
}
最小生成树的两个算法
Kruskal算法(适用条件:无向图)
算法思路:把所有边按权值从小到大排序,先选择权值最小的边,然后看有没有形成环,如果没有就保留这条边,然后再次选择除上次选择的边之外的所有边权值最小的边,再看有没有形成环,依此往下,形成环就不要这条边,把这条边排除,继续从剩下的边中选权值最小的,直到没有边了。
光看思路其实很简单,但是如何在代码中实现判断有没有形成环这个问题,这时候需要用到并查集。把所有点都存进一个单独的集合,这时候每个集合里只有一个点,可以看作是没有点是连通的,每选择一条边,先判断这条边的两个点是否存在于一个集合,如果不是就把这条边的两侧的点的集合合成一个集合,这个集合里就存放着这两个点,然后再选下一条边,如果这次选择的边的两个点存在于同一个集合,那么就形成的环,就排除这条边。
C++代码实现
unordered_set<Edge> kruskalMST(Graph graph)
{
UnionFind unionFind; //创建一个并查集,具体实现省略
unionFind.makeSets(graph.m_Nodes); //把每个点单独放进一个集合
priority_queue<Edge, vector<Edge>, EdgeCompare> priorityQueue; //利用谓词实现小根堆
for (auto edge : graph.m_Edges)
{
priorityQueue.push(edge);
}
unordered_set<Edge> result;
while (!priorityQueue.empty())
{
Edge cur = priorityQueue.top();
priorityQueue.pop();
if (!unionFind.isSameSet(cur.m_From, cur.m_To)) //判断这两个点是否属于同一个集合
{
result.insert(cur);
unionFind.unionSet(cur.m_From, cur.m_To); //把这两个点所属的集合结合成一个
}
}
return result;
}
Prim算法(适用条件:无向图)
算法思路:从源点开始,把源点记录下来,与源点相连的边被解锁,可以选择,其他都不能选择,在可以选择的边中选择权值最小的,记录进结果,把这条边从候选边中去掉,然后把这个边另外一个点记录下来,与新记录的点相连的边又被解锁,再从里面选择一条权值最小的,如果与这条边相连的两个点都被记录过,则放弃这条边,把这条边从候选边中去掉,如果有一个点没被记录过,则把这条边记录进结果,把另一个没被记录过的点记录下来。重复前面的内容,直到没有边可以选。
C++代码实现:
unordered_set<Edge> primMST(Graph graph)
{
priority_queue<Edge, vector<Edge>, EdgeCompare> priorityQueue;
unordered_set<Node> set; //记录联通的点
unordered_set<Edge> result;
for (auto nodePair : graph.m_Nodes) //避免出现森林的情况,把所有点都跑一遍,由于储存结果的容器是哈希表,所以不会储存相同的边
{
Node node = nodePair.second;
if (set.count(node) == 0)
{
set.insert(node);
for (Edge edge : node.m_Edges)
{
priorityQueue.push(edge);
}
while (!priorityQueue.empty())
{
Edge cur = priorityQueue.top();
priorityQueue.pop();
if (set.count(cur.m_To) == 0)
{
set.insert(cur.m_To);
result.insert(cur);
for (Edge nextEdge : cur.m_To.m_Edges)
{
priorityQueue.push(nextEdge);
}
}
}
}
}
return result;
}
Dijkstra算法(某个指定点到其他点的最短路径,适用条件:权值不能为负)(弗洛伊德算法没讲)
算法思路:如下图,A为指定点,右下角的表第一行代表图的各个点,第一列代表所指定的点,表里所填的值代表从A到其他点的举例,A到A的初始值是0,到其他点的初始值为+∞。每次选择这些距离值中最小的,是A的0,从A出发,看从A出发的边能不能让表里的值变得更小。A到B的举例就从+∞更新到0+3=3,到C的距离更新成0+15=15,到D的距离更新成0+9=9,到E的距离还是+∞。当使用完A的0值之后,这一列就被锁死,再也不使用了。然后除去锁死的列,从其他的值中选取最小的,是B的3,看从B出发的边能不能让表里的值变得更小,C变成了3+2=5,D不变,E变成了3+200=203。B的3用完了,这一列锁死。依次往后走,直到所有列都锁死。最后的表就是返回的结果
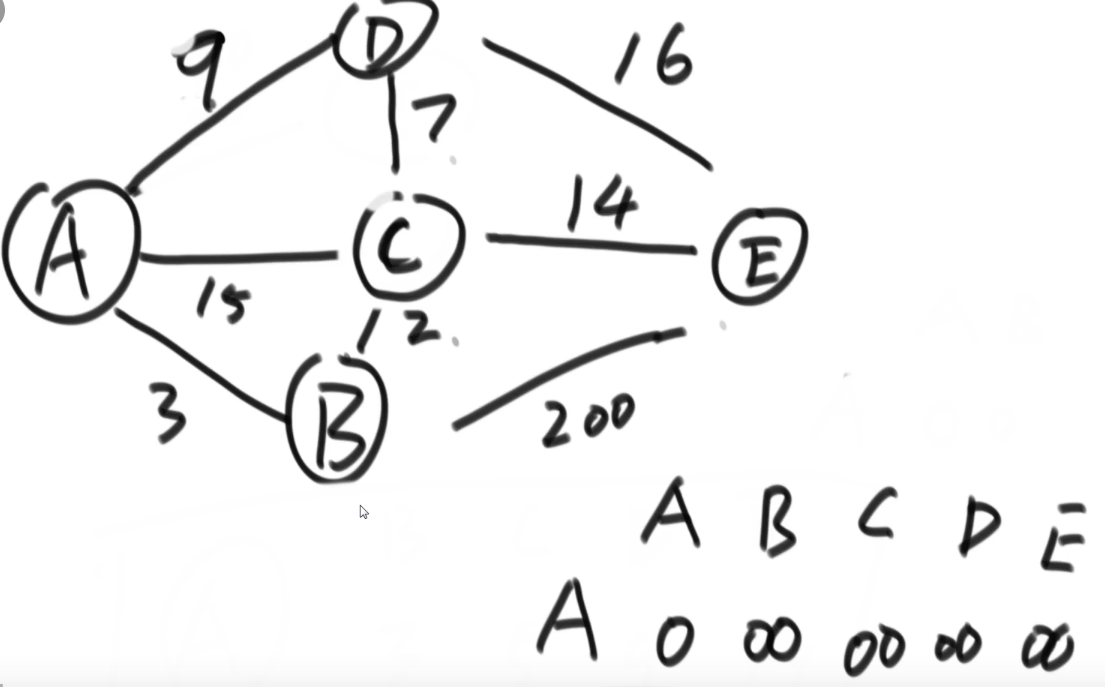
具体算法思路见https://www.bilibili.com/video/BV13g41157hK?p=9&vd_source=77d06bb648c4cce91c6939baa0595bcd P9 02:03:00
C++代码实现:
Node* getMinDistanceAndUnlockedNode(unordered_map<Node*, int> distanceMap, unordered_set<Node*> lockedNodes);
unordered_map<Node*, int> dijkstra(Node node)
{
unordered_map<Node*, int> distanceMap; //key代表图里的所有点,value代表指定点node到这些点的距离。
distanceMap.insert(make_pair(&node, 0));
unordered_set<Node*> lockedNodesSet; //已经求过最短距离,并“上锁”不需要再改动的节点
Node* minNode = getMinDistanceAndUnlockedNode(distanceMap, lockedNodesSet);
while (minNode != NULL)
{
for (Edge edge : minNode->m_Edges)
{
if (distanceMap.count(&edge.m_To) == 0)
{
distanceMap.insert(make_pair(&edge.m_To, distanceMap.at(minNode) + edge.m_Weight));
}
distanceMap.find(&edge.m_To)->second = distanceMap.find(&edge.m_To)->second < distanceMap.at(minNode) + edge.m_Weight ? distanceMap.find(&edge.m_To)->second : distanceMap.at(minNode) + edge.m_Weight;
}
lockedNodesSet.insert(minNode);
minNode = getMinDistanceAndUnlockedNode(distanceMap, lockedNodesSet);
}
return distanceMap;
}
Node* getMinDistanceAndUnlockedNode(unordered_map<Node*, int> distanceMap, unordered_set<Node*> lockedNodes)
{
Node* minNode = nullptr;
int minDistance = INT_MAX;
for (auto nodePair : distanceMap)
{
Node *node = nodePair.first;
int distance = distanceMap.at(nodePair.first);
if (lockedNodes.count(node) == 0 && distance < minDistance)
{
minNode = node;
minDistance = distance;
}
}
return minNode;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号