算法学习(11):二叉树(下)
二叉树
二叉树问题递归解题套路(可以解决所有树型DP(树型动态规划)题目)
- 问题可以通过往左子树要信息,往右子树要信息解决(从左边拿到信息,从右边拿到信息,然后汇总到根节点解决,比如从左边拿到高度和节点数,从右边拿到高度和节点数,汇总两边的信息得到整棵树的高度,然后看看是否符合节点数等于2的树的高度次方-1判断整棵树是不是满二叉树;或者有递归的感觉,比如判断一棵树是不是平衡二叉树,左子树需要是平衡二叉树,右子树需要平衡满二叉树)
- 列举成立的条件(左子树是平衡二叉树,右子树是平衡二叉树,左右子树的高度差不超过1,三个条件)
- 想需要从左子树和右子树拿到什么信息才能使上面列举的条件都成立(左右子树是不是平衡二叉树,左右子树的高度)
- 如果第3点左右两边需要拿到的信息不一样,则拿左右两边信息的全集
- 代码,首先考虑不需要递归的条件base case(例如head == NULL),然后调用左右子树的递归,返回信息。自己也要返回信息,利用左右子树返回的信息构建自己需要返回的信息。
判断一棵树是不是二叉搜索树
二叉搜索树的定义
二叉搜索树是一种特殊有序的二叉树,如果一棵树不为空,并且如果它的根节点左子树不为空,那么它左子树上面的所有节点的值都小于它的根节点的值,如果它的右子树不为空,那么它右子树任意节点的值都大于他的根节点的值,它的左右子树也是二叉搜索树。
中序遍历递归解法
思路:设置一个全局变量preValue,代表当前处理节点的上一个处理的节点的值,初始值为一个非常小的值。递归思路,首先调用递归函数判断左子树是否是二叉搜索树,如果不是就直接返回false,如果是则比较当前节点的值与preValue,如果比preValue小或相等,则返回false,如果大与preValue,则把preValue更新为当前节点的值,这时判断完左边都符合二叉搜索树,剩下右边了,所以返回右子树调用递归函数的结果。
long preValue = LONG_MIN; //考虑到leetcode用例越界问题 这里采用long
bool isValidBST(TreeNode* root)
{
if (root == NULL)
{
return true;
}
bool isBST = isValidBST(root->left);
if (!isBST)
{
return false;
}
if (root->val <= preValue)
{
return false;
}
preValue = root->val;
return isValidBST(root->right);
}
中序遍历非递归解法
思路:二叉树的非递归中序遍历,设置一个值preValue,代表当前处理节点的上一个处理的节点的值,初始值为非常小的值,假设是二叉搜索树,第一次打印时是在最小值处,此时与设置的上一个节点值preValue比较,如果当前值比preValue小或相等,则返回false,如果当前值比preValue大,则把preValue更新为当前节点的值,依次往下比较下去。
bool isValidBST2(TreeNode* head)
{
if (head != NULL)
{
stack<TreeNode*> treeNodeStack;
long preValue = LONG_MIN; //考虑到leetcode用例越界问题 这里采用long
while (!treeNodeStack.empty() || head != NULL)
{
if (head != NULL)
{
treeNodeStack.push(head);
head = head->left;
}
else
{
head = treeNodeStack.top();
treeNodeStack.pop();
if (head->val <= preValue)
{
return false;
}
else
{
preValue = head->val;
}
head = head->right;
}
}
}
return true;
}
递归套路解
- 条件:左子树是二叉搜索树,右子树是二叉搜索树,左子树的最大值小于当前节点值,右子树的最小值大于当前节点值
- 需要拿到的信息:左右子树是否是二叉搜索树,左子树的最大值,右子树的最小值
- 取全集,子树是否是二叉搜索树,子树的最大值和最小值
C++代码实现:
class Info
{
public:
Info(){}
Info(bool isBST, int max, int min)
{
this->m_IsBST = isBST;
this->m_Max = max;
this->m_Min = min;
}
public:
bool m_IsBST;
int m_Max;
int m_Min;
};
Info process(TreeNode* head);
bool isValidBST3(TreeNode* head)
{
if (head == NULL)
{
return true;
}
return process(head).m_IsBST;
}
Info process(TreeNode* head)
{
if (head == NULL)
{
return Info(true,INT_MIN,INT_MAX); //int类型有可能溢出,此时需要选择更多位数类型的最大最小值,class里也要改
}
Info leftData = process(head->left);
Info rightData = process(head->right);
int max = head->val > leftData.m_Max ? head->val : leftData.m_Max;
max = max > rightData.m_Max ? max : rightData.m_Max;
int min = head->val < leftData.m_Min ? head->val : leftData.m_Min;
min = min < rightData.m_Min ? min : rightData.m_Min;
bool isBST = false;
if (leftData.m_IsBST && rightData.m_IsBST && leftData.m_Max < head->val && rightData.m_Min > head->val)
{
isBST = true;
}
return Info(isBST, max, min);
}
判断一棵树是否是完全二叉树
完全二叉树的定义
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
非递归解法
思路:层序遍历这棵树,只要出现一个节点左子树为空,右子树不为空,直接返回false,当遇到第一个左子树不为空,右子树为空的节点时,后面的所有节点都是叶子节点,即左右子树都为空,如果出现左右子树不都为空的情况,返回false。
bool isCompleteBinaryTree(TreeNode* head)
{
if (head != NULL)
{
bool leaf = false;
queue<TreeNode*> treeNodeQueue;
treeNodeQueue.push(head);
while (!treeNodeQueue.empty())
{
TreeNode* cur = treeNodeQueue.front();
treeNodeQueue.pop();
if ((leaf && (cur->left == NULL || cur->right == NULL)) || (cur->left == NULL && cur->right != NULL))
{
return false;
}
if (cur->left != NULL)
{
treeNodeQueue.push(cur->left);
}
if (cur->right != NULL)
{
treeNodeQueue.push(cur->right);
}
if (cur->left == NULL || cur->right == NULL)
{
leaf = true;
}
}
}
return true;
}
判断一棵树是否是满二叉树
简单方法思路
得到这棵树的深度d,得到这棵树的节点数l,如果是满二叉树,则满足l = 2d + 1
递归套路解
- 条件:左右子树都是满二叉树,左右子树的高度一样
- 需要拿到的信息:左右子树是否是满二叉树,左右子树的高度
C++代码实现
class Info
{
public:
Info(){}
Info(bool isFBT, int high)
{
this->m_IsFBT = isFBT;
this->m_High = high;
}
public:
bool m_IsFBT;
int m_High;
};
Info process(TreeNode* head);
bool isFBT(TreeNode* head)
{
if (head == NULL)
{
return true;
}
return process(head).m_IsFBT;
}
Info process(TreeNode* head)
{
if (head == NULL)
{
return Info(true, 0);
}
Info leftData = process(head->left);
Info rightData = process(head->right);
int high = (leftData.m_High > rightData.m_High ? leftData.m_High : rightData.m_High) + 1;
bool isFBT = false;
if (leftData.m_IsFBT && rightData.m_IsFBT && (leftData.m_High == rightData.m_High))
{
isFBT = true;
}
return Info(isFBT, high);
}
判断一棵树是不是平衡二叉树
平衡二叉树的定义
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
递归套路解
- 条件:左子树是平衡二叉树,右子树是平衡二叉树,左子树的高度与右子树的高度差不超过1
- 需要的信息:左右子树是否是平衡二叉树,左右子树的高度
C++代码实现:
class Info
{
public:
Info(){}
Info(bool isAVL, int high)
{
this->m_IsAVL = isAVL;
this->m_High = high;
}
public:
bool m_IsAVL;
int m_High;
};
Info process(TreeNode* head);
bool isAVL(TreeNode* head)
{
if (head == NULL)
{
return true;
}
return process(head).m_IsAVL;
}
Info process(TreeNode* head)
{
if (head == NULL)
{
return Info(true, 0);
}
Info leftData = process(head->left);
Info rightData = process(head->right);
int high = (leftData.m_High > rightData.m_High ? leftData.m_High : rightData.m_High) + 1;
bool isAVL = false;
if (leftData.m_IsAVL && rightData.m_IsAVL && (abs(leftData.m_High - rightData.m_High)) < 2)
{
isAVL = true;
}
return Info(isAVL, high);
}
给定两个二叉树的节点node1和node2,找到他们的最低公共祖先节点
什么叫最低公共祖先?
给定的两个点往上最初汇聚到的点就叫最低公共祖先
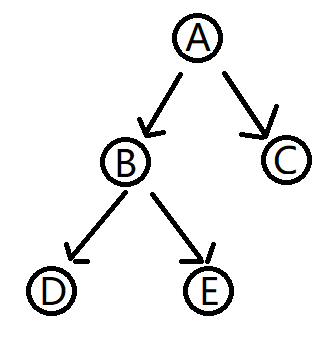
如上图所示的树,D和E的最低公共祖先是B,B和E的最低公共祖先是B,E和C的最低公共祖先是A
简单但是复杂度高的解法
准备一个hashmap,存放所有点的父节点,key值存放节点,value存放key的父节点。遍历一遍树,把所有点的父节点都统计一遍(不要忘记最上面的根节点head的父节点是自己,根据代码实现的不同可能需要单独存放一遍),然后准备一个hashset,从给定的node1节点开始往上走,把走过的所有点统计一遍(包括node1和head),然后node2开始往上走,每走一步就在hashset里找当前节点是否存在,最先找到的存在的那个就是最低公共祖先。(代码省略了)
复杂度低的算法
二叉树递归套路思想可以往左右要信息,查找左右是否含有node1和node2
- 最低公共祖先的条件:第一个(深度最深的)左子树和右子树同时含有node1和node2的节点
- 需要的信息:左右子树是否含有node1或node2
代码实现的思路:递归的返回是一个节点,如果左右子树或者自己含有node1就返回node1,如果含有node2就返回node2,都有(左右递归返回值都不为空,即找到了第一个(深度最深的)左子树和右子树同时含有node1和node2的节点)就返回当前这个节点(就是所要求的最低公共祖先),其余全都返回空,base case是遇到空或者node1、node2就返回自己,因为如果node1和node2互为公共祖先(即上图中B与E的关系)则遇到最上面的点时,就不会遇到下面的点,而此时根节点A的左子树返回B,右子树一定返回空,最后就会返回B,而B就是最终答案。
以上的代码思路是经过优化的思路,需要多看多记,具体思路见https://www.bilibili.com/video/BV13g41157hK?p=8&vd_source=77d06bb648c4cce91c6939baa0595bcd P8 01:33:17
C++代码实现:
TreeNode* lowestCommonAncestor(TreeNode* head, TreeNode* node1, TreeNode* node2)
{
if (head == NULL || head == node1 || head == node2)
{
return head;
}
TreeNode* left = lowestCommonAncestor(head->left, node1, node2);
TreeNode* right = lowestCommonAncestor(head->right, node1, node2);
if (left != NULL && right != NULL)
{
return head;
}
return left != NULL ? left : right;
}
在二叉树中找到一个节点node的后继节点(二叉树节点的结构中有一个指向父节点的指针),如果node到它后继节点的距离是K,保证时间复杂度为0(K)。
什么是二叉树中一个节点的后继节点
中序遍历中一个节点的下一个节点
解题思路
分两种情况讨论:
- 当node有右子树时:node的后继节点就是右子树中最左边的节点。因为中序遍历,打印完node这个“中”之后,又该会去node的右子树做“右”,而“右”又会被分解成“左中右”,所以下一步会去打印右子树的最左节点。
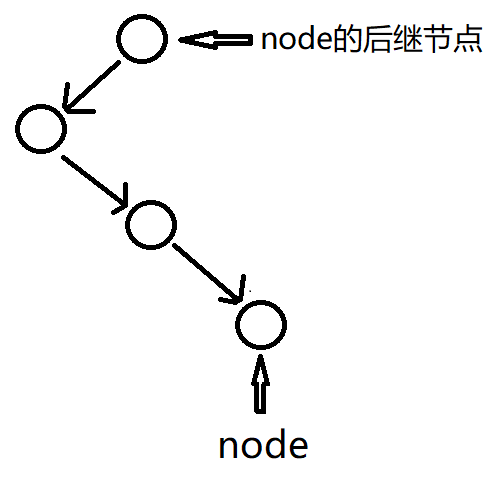
- 当node没有右子树时:从node开始往上走,当走到的当前节点cur不是它父节点的右孩子的时候,cur的父节点就是node的后继节点。因为中序遍历的顺序“左中右”,“左”分解为“左中右”,因为node没有右子树,所以这时“左”打印完了,要去找“中”,cur的父节点就是“中”,如下图所示。但是还有一种情况,就是中序遍历的最后一个节点,它没有后继节点,它也没有右子树,这时需要判断
![]()
C++代码实现:
TreeNode* inorderSuccessor(TreeNode* head, TreeNode* node)
{
if (node == NULL)
{
return NULL;
}
if (node->right != NULL)
{
TreeNode* cur = node->right;
while (cur->left != NULL)
{
cur = cur->left;
}
return cur;
}
else
{
TreeNode* parent = node->parent;
while (parent == NULL || parent->right != node)
{
node = node->parent;
parent = node->parent;
}
return parent;
}
}
二叉树的序列化和反序列化
什么是序列化和反序列化
序列化简单地说就是把二叉树转化为一串字符串,这串字符串可以确定一个唯一结构的树;反序列化就是把这串字符串转化为二叉树
思路
- 序列化:空节点用“#”记录,每个节点之间用“_”分割,选择一种遍历方式,遍历二叉树,返回最后的一串字符串
- 反序列化:把字符串按“”分割依次存进队列(队列里存节点的值和“#”,不存放“”),然后消费队列利用递归方法建立树
C++代码实现:
string serialize(TreeNode* root)
{
if (root == NULL)
{
return "#_";
}
string res = to_string(root->val) + "_";
res += serialize(root->left);
res += serialize(root->right);
return res;
}
TreeNode* buildTree(queue<string> &valQue);
TreeNode* deserialize(string data)
{
queue<string> valQue;
while (data != "")
{
valQue.push(data.substr(0, data.find("_")));
data.erase(0, data.find("_") + 1);
}
return buildTree(valQue);
}
TreeNode* buildTree(queue<string> &valQue)
{
string val = valQue.front();
valQue.pop();
if (val == "#")
{
return NULL;
}
TreeNode* node = new TreeNode(stoi(val));
node->left = buildTree(valQue);
node->right = buildTree(valQue);
return node;
}
微软面试原题:折纸问题
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时折痕是凹下去的,即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。给定一个输入参数N,代表纸条都从下边向上方连续对折N次。请从上到下打印所有折痕的方向。例如:N=1时,打印: down N=2时,打印: down down up
解题思路
第一次对折的折痕记作1down,每次对折,上一次新出现的折痕的上面会出现一个down,下面会出现一个up,这与上一次的折痕是down还是up无关。
所以对折的结果会是:
- 1down
- (2down 1down 2up)
- (3down 2down 3up ) 1down (3down 2up 3up)
- …………
仔细观察,这其实是一颗满二叉树,所以题干中要求的从上到下打印其实就是这颗N层满二叉树的中序遍历。
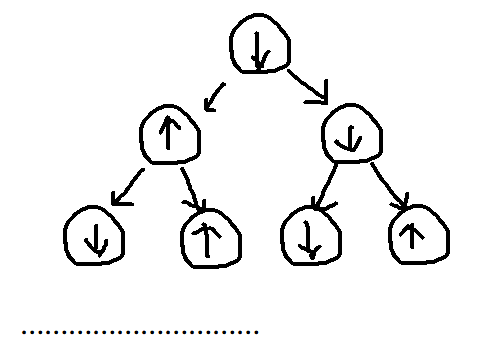
这颗满二叉树满足这样的条件:每一个非叶节点的左孩子为down,右孩子为up。
C++代码实现
void print(int level, int N, bool dire);
void paperFolding(int N)
{
print(1, N, true);
}
void print(int level, int N, bool dire)
{
if (level > N)
{
return;
}
print(level + 1, N, true);
string ans = dire ? "凹" : "凸";
cout << ans << " ";
print(level + 1, N, false);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号