算法学习（10）：二叉树（上）

二叉树

二叉树的递归序

void  f(TreeNode* head)
{   //第一次
    if (head == NULL)
    {
        return;
    }
    //第一次
    f(head->left);
    //第二次
    //第二次
    f(head->right);
    //第三次
    //第三次
}

这是一个二叉树的遍历函数，注释中的第N次代表到达这个节点的次数，假设每到达一次就打印一次，则下图这样的树的递归序为

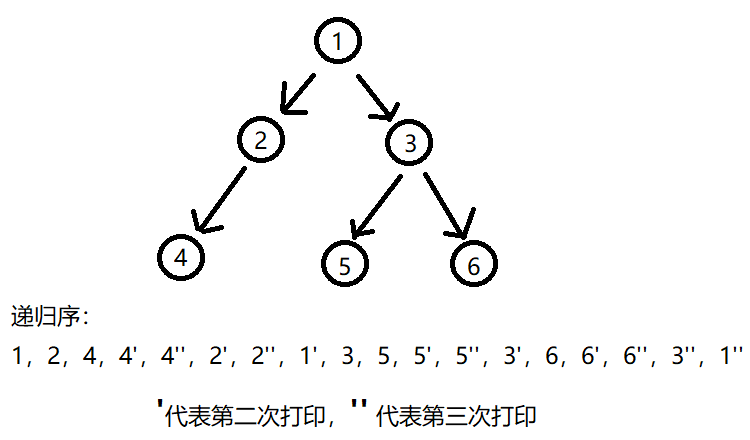
二叉树的先序、中序、后序遍历都是由递归序改成的，先序遍历是只留下递归序的第一次打印，中序是只留下第二次，后序是只留下第三次。

二叉树的先序、中序、后续遍历的递归代码实现（C++）

先序

void  preorderTraversal(TreeNode* head)
{
    if (head == NULL)
    {
        return;
    }
    printTreeNode(head);  //打印此节点（后面的此函数含义一样，不再赘述）
    preorderTraversal(head->left);
    preorderTraversal(head->right);
}

中序

void  inorderTraversal(TreeNode* head)
{
    if (head == NULL)
    {
        return;
    }
    preorderTraversal(head->left);
    printTreeNode(head);
    preorderTraversal(head->right);
}

后序

void  postorderTraversal(TreeNode* head)
{
    if (head == NULL)
    {
        return;
    }
    preorderTraversal(head->left);
    preorderTraversal(head->right);
    printTreeNode(head);
}

先序、中序、后续遍历的非递归实现

先序

思路：准备一个栈，先把树的根节点压栈，然后进循环，弹出一个节点，打印，然后先把这个弹出节点的右孩子进栈，再左孩子进栈，进下一次循环，直到栈为空
C++实现代码：

void  nonrecursivePreorderTraversal(TreeNode* head)
{
    if (head != NULL)
    {
        stack<TreeNode*> treeNodeStack;
            treeNodeStack.push(head);
        while (!treeNodeStack.empty())
        {
            TreeNode* cur = treeNodeStack.top();
            treeNodeStack.pop();
            printTreeNode(cur);
            if (cur->right != NULL)
            {
                treeNodeStack.push(cur->right);
            }
            if (cur->left != NULL)
            {
                treeNodeStack.push(cur->left);
            }
        }
    }
}

后序

先说后序的思路：基本思路与先序一样，再额外准备一个收集栈，在先序思路里打印的时候不打印，而是压入额外准备的收集栈，然后先把刚压入节点的左孩子压进第一个栈，再压有孩子进第一个栈，周而复始，直到第一个栈空了，然后打印收集栈的节点。因为收集栈里压入的顺序是头右左，出栈就是左右头（后序）。
C++实现代码：

void  nonrecursivePostorderTraversal(TreeNode* head)
{
    if (head != NULL)
    {
        stack<TreeNode*> treeNodeStack1;
        stack<TreeNode*> treeNodeStack2;
        treeNodeStack1.push(head);
        while (!treeNodeStack1.empty())
        {
            TreeNode* cur = treeNodeStack1.top();
            treeNodeStack1.pop();
            treeNodeStack2.push(cur);
            if (cur->left != NULL)
            {
                treeNodeStack1.push(cur->left);
            }
            if (cur->right != NULL)
            {
                treeNodeStack1.push(cur->right);
            }
        }
        while (!treeNodeStack2.empty())
        {
            printTreeNode(treeNodeStack2.top());
            treeNodeStack2.pop();
        }
    }
}

中序

思路

准备一个栈，从根节点依次往左，把所有节点入栈，到空开始弹出，弹出时打印，然后再把弹出的节点的右节点入栈，右节点当作根节点，重复前面的内容。

为什么这种思路可以做到中序遍历

因为这种思路压栈的顺序的“中 左”，打印的时候就是“左中”，而每次到“中”的时候，就会往右走，“右”又被分解成“左中”，如下图

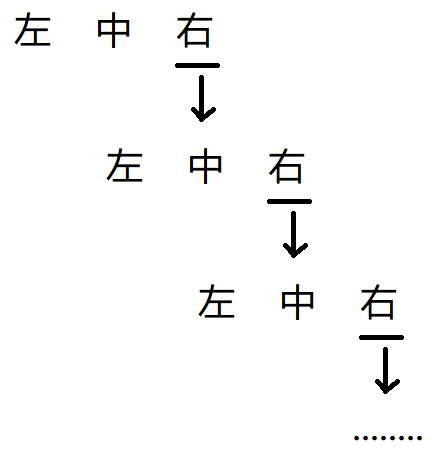
“右”一直被分解成“左中”，这样就做到了中序遍历。

C++代码实现（代码经过优化，如果忘记要多看）

void  nonrecursiveInorderTraversal(TreeNode* head)
{
    if (head != NULL)
    {
        stack<TreeNode*> treeNodeStack;
        while (!treeNodeStack.empty() || head != NULL)
        {
            if (head != NULL)
            {
                treeNodeStack.push(head);
                head = head->left;
            }
            else
            {
                head = treeNodeStack.top();
                treeNodeStack.pop();
                printTreeNode(head);
                head = head->right;
            }
        }
    }
}

二叉树的宽度优先遍历

什么是层序遍历

所谓宽度优先遍历，就是层序遍历，一层一层输出。

思路

准备一个队列，先根节点入队列，然后弹出，弹出时打印，然后把弹出节点的左孩子入队列，再把右孩子入队列，然后再弹出周而复始。

C++代码实现

void levelTraversal(TreeNode* head)
{
    if (head != NULL)
    {
        queue<TreeNode*> treeNodeQueue;
        treeNodeQueue.push(head);
        while (!treeNodeQueue.empty())
        {
            TreeNode* cur = treeNodeQueue.front();
            treeNodeQueue.pop();
            printTreeNode(cur);
            if (cur->left != NULL)
            {
                treeNodeQueue.push(cur->left);
            }
            if (cur->right != NULL)
            {
                treeNodeQueue.push(cur->right);
            }
        }
    }
}

常见题目：求一颗二叉树的宽度

如这样一个二叉树的最大宽度就是2

使用哈希表的算法

思路：准备一个哈希表，哈希表里key值是节点，value是层数；一个值max，记录最大宽度，初始值是0；一个值curLevel，记录当前层数；一个值nodes，记录当前层的节点数，初始值是0。首先把根节点存到哈希表里并入队列，开始出队列，记录这个节点，然后和当前层数比较，如果一样，nodes++，如果不一样，当前层数变为curLevel+1，nodes与max比较，max存较大的那个，nodes重置为1。将记录的当前出队列的节点的左右孩子入队列（如果有的话），并存进哈希表，value值为curLevel+1，重复循环。当循环结束时，还要比较一下最后一层的nodes和max的值的大小，返回较大的那个。
具体算法思路见https://www.bilibili.com/video/BV13g41157hK?p=7&vd_source=77d06bb648c4cce91c6939baa0595bcd P7 01：57：10

int maxWidth(TreeNode* head)
{
    if (head != NULL)
    {
        queue<TreeNode*> treeNodeQueue;
        unordered_map<TreeNode*, int> treeNodeMap;
        treeNodeQueue.push(head);
        treeNodeMap.insert(make_pair(head, 0));
        int max = 0, curLevel = 0, nodes = 0;
        while (!treeNodeQueue.empty())
        {
            TreeNode* cur = treeNodeQueue.front();
            treeNodeQueue.pop();
            if (curLevel == treeNodeMap.find(cur)->second)
            {
                nodes++;
            }
            else
            {
                curLevel++;
                max = nodes > max ? nodes : max;
                nodes = 1;
            }
            if (cur->left != NULL)
            {
                treeNodeQueue.push(cur->left);
                treeNodeMap.insert(make_pair(cur->left, treeNodeMap.find(cur)->second + 1));
            }
            if (cur->right != NULL)
            {
                treeNodeQueue.push(cur->right);
                treeNodeMap.insert(make_pair(cur->right, treeNodeMap.find(cur)->second + 1));
            }
        }
        max = nodes > max ? nodes : max;  //统计最后一层的情况
        return max;
    }
}

不用哈希表的算法

思路：准备一个队列；一个节点curEnd，储存当前层的最后一个节点，初始值是二叉树的根节点；一个节点nextEnd，储存下一层的最后一个节点，初始值是NULL；一个值max，记录最大宽度，初始值是0；一个值nodes，记录当前层的节点数，初始值是0；首先把根节点入队列，然后入循环，出队列，记录出队列的当前节点为cur，当前节点如果有左孩子，入队列，如果nextEnd是空，将nextEnd更新为左孩子，当前节点如果有右孩子，入队列，将nextEnd更新为右孩子，每入队列一个节点，就把nextEnd更新成这个节点。nodes++。然后判断当前节点cur是不是当前层最后一个节点curEnd，如果是就把nextEnd赋给curEnd，max储存max与nodes之间大的那个，nodes归零。进下一次循环，直到队列为空。
具体算法思路见https://www.bilibili.com/video/BV13g41157hK?p=7&vd_source=77d06bb648c4cce91c6939baa0595bcd P7 02：11：10

int maxWidth(TreeNode* head)
{
    if (head != NULL)
    {
        queue<TreeNode*> treeNodeQueue;
        treeNodeQueue.push(head);
        TreeNode* curEnd = head;
        TreeNode* nextEnd = NULL;
        int max = 0, nodes = 0;
        while (!treeNodeQueue.empty())
        {
            TreeNode* cur = treeNodeQueue.front();
            treeNodeQueue.pop();
            if (cur->left != NULL)
            {
                treeNodeQueue.push(cur->left);
                nextEnd = cur->left;
            }
            if (cur->right != NULL)
            {
                treeNodeQueue.push(cur->right);
                nextEnd = cur->right;
            }
            nodes++;
            if (cur == curEnd)
            {
                curEnd = nextEnd;
                max = nodes > max ? nodes : max;
                nodes = 0;
            }
        }
        return max;
    }
}