算法学习(9):链表
链表
链表前言
重要技巧:额外数据结构记录(哈希表),快慢指针
链表结构C++代码(以下算法题的所有解都是由C++代码完成):
struct ListNode
{
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
快慢指针技巧
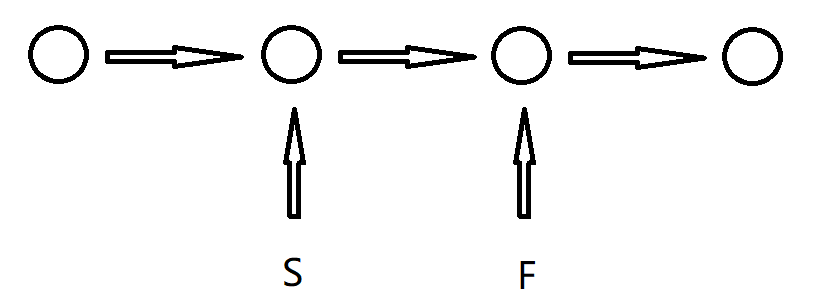
- 当链表长度为奇数时,快指针F和慢指针S开始指向链表头,while循环条件为S->next != NULL && F->next->next != NULL,这样最后S会停在最中间的位置,F会停在最后的位置
- 当链表长度为偶数时。如果想让S停在中间靠左的位置
![]()
方法与1一样,这时F会停在倒数第二个节点的位置,如果想让F停在最后的节点,则在循环结束加一个判断语句,如果F节点的下一个节点不是空,则F向后移动一个节点;如果想让S停在中间靠右的位置,则判断F节点的下一个节点是不是空,如果不是,把S向后移动一个节点,想让F停在最后则也让F向后移动一个节点。 - 当链表长度小于等于2时,上面的方法同样适用。
题目(1):反转单向链表
(1)最简单的办法,栈。思路:遍历链表,将节点进栈,然后出栈串起来。
ListNode* reverseList(ListNode* head)
{
stack<int> stack;
while (head != NULL)
{
stack.push(head->val);
head = head->next;
}
ListNode* newHead =new ListNode(-1);
ListNode* body = newHead;
while (!stack.empty())
{
body->next = new ListNode(stack.top());
stack.pop();
body = body->next;
}
return newHead->next;
}
(2)迭代。思路:准备两个指针,一个cur指针指向当前节点,一个pre指针指向当前节点的上一个节点。遍历数组,首先记录当前节点的下一个节点,然后将当前节点指向上一个节点pre,然后pre指向当前节点cur,当前节点cur指向最开始记录的下一个节点,直到cur为空为止。
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
ListNode* cur = head;
while (cur != NULL)
{
ListNode* next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
题目(2):给定两个链表的头指针head1和head2,打印两个有序链表的公共部分,要求时间复杂度为O(N),额外空间复杂度为O(1)
思路:准备两个指针,分别指向head1和head2,谁指到的节点的值小,谁往后移动,遇到相等的就打印,然后同时向后移动,直到一个指针为空。
void printSamePart(ListNode* head1, ListNode* head2)
{
ListNode* p1 = head1;
ListNode* p2 = head2;
while (p1 != NULL && p2 != NULL)
{
if (p1->val < p2->val)
{
p1 = p1->next;
}
else if (p1->val = p2->val)
{
cout << p1->val << " ";
p1 = p1->next;
p2 = p2->next;
}
else
{
p2 = p2->next;
}
}
}
题目(3):判断一个链表是否是回文结构
(1)简单解法思路:遍历链表,把每个节点上的值入栈,然后从链表头从新开始,与栈顶值比对,相同就往下走,栈pop,一旦出现不同,返回false,否则就是true。
bool isPalindrome(ListNode* head)
{
stack<int> stack;
ListNode* p = head;
while (p != NULL)
{
stack.push(p->val);
p = p->next;
}
while (head != NULL)
{
if (head->val != stack.top())
{
return false;
}
head = head->next;
stack.pop();
}
return true;
}
(2)比简单方法稍微省一点空间的方法:利用上文中提到的快慢指针技巧2,如果链表长度是偶数就把慢指针S停在中间靠右的位置,然后把从S指针开始向后遍历进栈,遍历完后开始从链表head开始与栈顶元素比较,相同就出栈然后节点后移,只要出现不同就返回false,直到栈空,返回true。
(3)最佳方法思路:利用上文中提到的快慢指针技巧2,如果链表长度是偶数就把慢指针S停在中间靠右的位置,然后从S开始把后面的节点逆序,注意S指向的中间节点逆序后的结果要指向NULL。
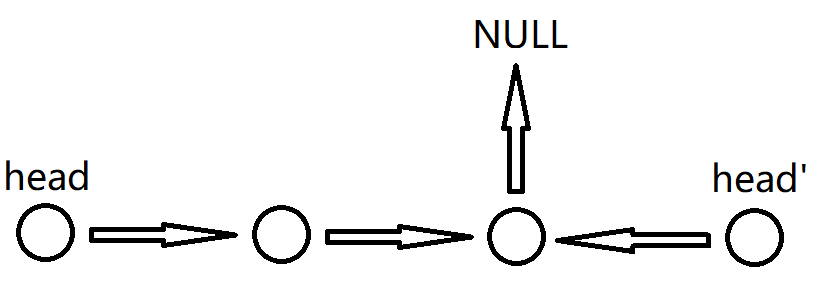
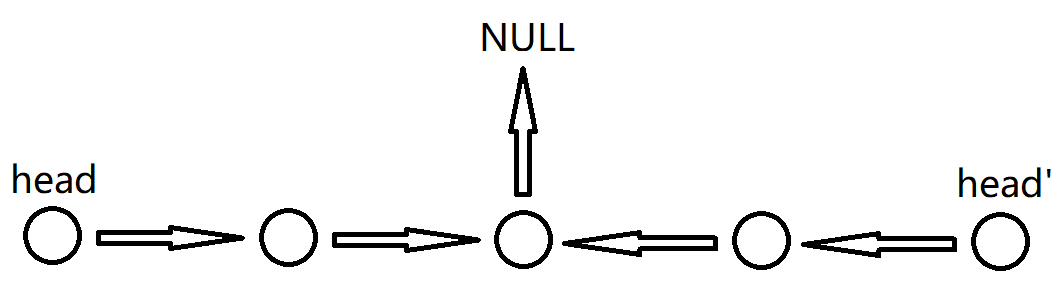
然后从head和head'开始两边遍历并且比较是否相等,只要出现不同就返回false,直到其中一个为空,然后把反转的链表复原,最后返回true
bool isPalindrome(ListNode* head)
{
ListNode* F = head;
ListNode* S = head;
while (F->next != NULL && F->next->next != NULL)
{
F = F->next->next;
S = S->next;
}
if (F->next != NULL)
{
S = S->next;
}
F = nullptr;
while (S != NULL)
{
ListNode* node = S->next;
S->next = F;
F = S;
S = node;
}
ListNode* head2 = F;
ListNode* node = head;
bool res = true;
while (node != NULL && F != NULL)
{
if (node->val != F->val)
{
res = false;
break;
}
node = node->next;
F = F->next;
}
while (head2 != NULL)
{
ListNode* temp = head2->next;
head->next = F;
F = head2;
head2 = temp;
}
return res;
}
题目(4):将单向链表按给定的某值划分成左边小,中间相等,右边大的形式
(1)最简单的方法思路:创建一个node数组,把链表的节点放进数组,然后partition,最后再串起来。
ListNode* nodeArrPartition(ListNode* head ,int pivot)
{
vector<ListNode> nodeArr;
ListNode* p = head;
int length = 0;
while (p != NULL);
{
nodeArr.push_back(*p);
p = p->next;
length++;
}
if (nodeArr.size() != NULL)
{
int left = -1;
int right = length;
for (int i = 0; i < right;)
{
if (nodeArr[i].val < pivot)
{
swap(nodeArr, i++, ++left);
}
else if (nodeArr[i].val = pivot)
{
i++;
}
else
{
swap(nodeArr, i, --right);
}
}
for (int i = 0; i < length - 1; i++)
{
nodeArr[i].next = &nodeArr[i + 1];
}
nodeArr[length - 1].next = nullptr;
return &nodeArr[0];
}
}
(2)时间复杂度O(N),额外空间复杂度O(1)的做法。
思路:准备六个变量,小于部分的头尾sH、sT,等于部分的头尾eH、eT,大于部分的头尾mH、mT,六个变量一开始都是空。从头开始遍历,将节点的值与pivot比较,然后看属于哪一部分,再看那部分的头和尾是不是空,是空就头尾都等于当前节点,不是空就把尾巴节点指向当前节点,然后把尾巴节点更新为当前节点,继续遍历周而复始,直到遍历完。然后把小于部分的尾连接等于部分的头,等于部分的尾连接大于部分的头,最后返回小于部分的头即可。
详细思路见https://www.bilibili.com/video/BV13g41157hK?p=6&vd_source=77d06bb648c4cce91c6939baa0595bcd P6 01:36:30
ListNode* nodePartition(ListNode* head, int pivot)
{
ListNode* sH = NULL;
ListNode* sT = NULL;
ListNode* eH = NULL;
ListNode* eT = NULL;
ListNode* mH = NULL;
ListNode* mT = NULL;
ListNode* next = NULL;
while (head != NULL)
{
next = head->next;
head->next = NULL;
if (head->val < pivot)
{
if (sH == NULL)
{
sH = head;
sT = head;
}
else
{
sT->next = head;
sT = head;
}
}
else if (head->val > pivot)
{
if (mH == NULL)
{
mH = head;
mT = head;
}
else
{
mT->next = head;
mT = head;
}
}
else
{
if (eH == NULL)
{
eH = head;
eT = head;
}
else
{
eT->next = head;
eT = head;
}
}
head = next;
}
if (sH == NULL)
{
if (eH == NULL)
return mH;
else
{
eT->next = mH;
return eH;
}
}
else
{
if (eH == NULL)
{
sT->next = mH;
return sH;
}
else
{
sT->next = eH;
eT->next = mH;
return sH;
}
}
//最后连接部分的简洁写法
//if (sT != NULL)
//{
// sT->next = eH;
// eT = eT == NULL ? sT : eT;
//}
//if (eT != NULL)
//{
// eT->next = mH;
//}
//return sH != NULL ? sH : (eH != NULL ? eH : mH);
}
题目(5):复制含有随即指针节点的链表
(1)最简单的思路:遍历链表,然后放进hashmap里,key是原来链表的节点,value是深拷贝的新节点(先只设置值),然后再从头遍历链表,每遍历一个节点,就利用旧节点通过哈希表找到新节点,新节点的next指针就指向利用旧节点的next指针找到的哈希表对应的下一个新节点,random指针同样,最后返回利用head找到的哈希表的新节点。
Node* copyRandomList(Node* head)
{
unordered_map<Node*, Node*> hashmap;
Node* p = head;
while (p != NULL)
{
hashmap.insert(make_pair(p, new Node(p->val)));
p = p->next;
}
p = head;
while (p != NULL)
{
hashmap[p]->next = hashmap[p->next];
hashmap[p]->random = hashmap[p->random];
p = p->next;
}
return hashmap[head];
}
(2)时间复杂度O(N),额外空间复杂度O(1)的做法
思路:遍历链表,然后在旧节点后面加一个深拷贝的新节点(只先设置值),由新节点连接后面的节点
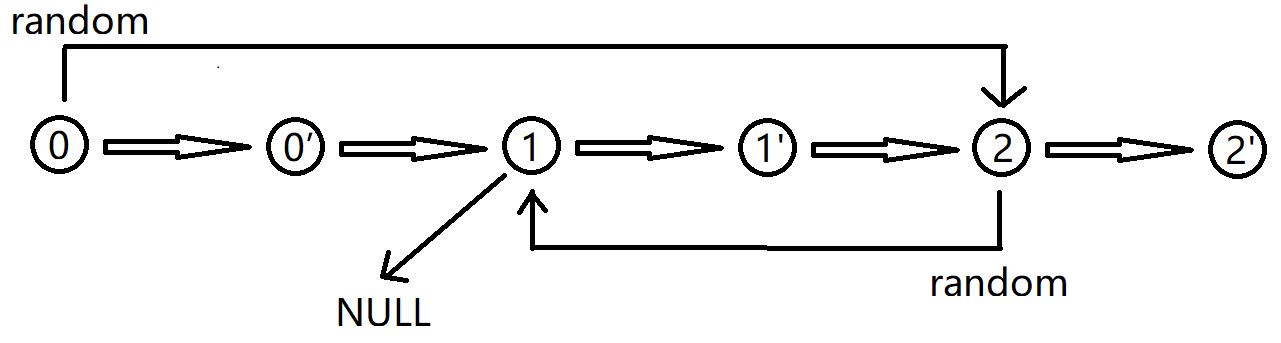
遍历新链表的时候可以一对一对地取,然后可以通过旧节点的random指针指向的节点的next指针指向的新节点找到拷贝的random节点。遍历完之后再把新旧节点分离。
详细思路见https://www.bilibili.com/video/BV13g41157hK?p=6&vd_source=77d06bb648c4cce91c6939baa0595bcd P6 01:53:10
Node* copyRandomList(Node* head)
{
if (head == NULL)
{
return NULL;
}
Node* cur = head;
while (cur != NULL)
{
Node* next = new Node(cur->val);
next->next = cur->next;
cur->next = next;
cur = cur->next->next;
}
Node* curCopy;
cur = head;
while (cur != NULL)
{
curCopy = cur->next;
curCopy->random = cur->random == NULL ? NULL : cur->random->next;
cur = cur->next->next;
}
cur = head;
Node* res = head->next;
while (cur != NULL)
{
Node* temp = cur->next->next;
cur->next->next = temp == NULL ? NULL : temp->next;
cur->next = temp;
cur = cur->next;
}
return res;
}
题目(6):两个链表相交的一系列问题
【题干】给定两个可能有环也可能无环的单链表,头节点head1和head2。请实现一个函数,如果两个链表相交,请返回相交的第一个节点。如果不相交,返回NULL。要求时间复杂度O(N),额外空间复杂度O(1)。
思路:首先解决有环还是无环,两种思路:
- 不考虑额外空间复杂度:创建一个哈希表,然后遍历链表,遍历时先在哈希表里找当前节点是否存在,不存在就把当前节点存进哈希表,然后节点后移。找到相同的节点证明有环,并返回这个节点,这是入环第一个节点;链表遍历完了证明无环。
- 额外空间复杂度O(1):快慢指针,快指针一次走两步,慢指针一次走一步,循环遍历,循环条件是快指针不等于慢指针并且快指针不为NULL,如果有环则快慢指针必在环内相遇。所以如果跳出循环的原因是快指针变为NULL了则无环,否则就有环。当快慢指针相遇时,快指针从head开始重新遍历,慢指针继续遍历,当快慢指针再次相遇时,这个节点就是入环节点(数学证明见leetcode剑指 Offer II 022. 链表中环的入口节点),返回这个节点
解决完有环无环之后,分情况讨论:
-
如果一个有环一个无环,则必定不可能相交,返回NULL;
-
如果都无环,两个链表都遍历一遍,并分别记录链表长度length1和length2,然后看最后一个节点一不一样。不一样则必定不相交,返回NULL;如果一样,则相交,然后再次从头开始遍历,长度长的先遍历,先走|length1 - length2|步,然后短的链表开始走,当两个链表遍历到一样的节点时,这个节点就是相交的第一个节点,返回这个节点。
-
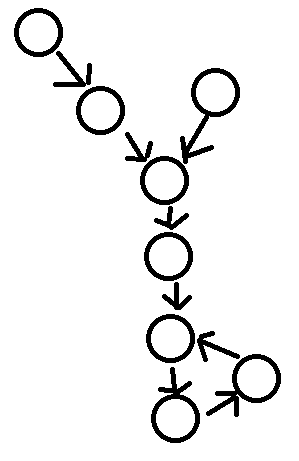
如果都有环,看入环节点是否一样,如果入环节点一样,那么就是下面这种情况
![]()
这种情况就跟两个链表都无环且相交的情况一样,把入环节点当作链表结尾就行了。
如果不一样,那么就是下面这种情况
![]() 这时从其中一个链表的入环节点loop1继续循环往下遍历,如果loop2相遇了,那么一定是情况(2),此时返回loop2即可,因为loop1和loop2都是第一个相交节点。如果转了一圈走回到了loop1还没遇到loop2,那么就是情况(1),返回NULL
这时从其中一个链表的入环节点loop1继续循环往下遍历,如果loop2相遇了,那么一定是情况(2),此时返回loop2即可,因为loop1和loop2都是第一个相交节点。如果转了一圈走回到了loop1还没遇到loop2,那么就是情况(1),返回NULL
详细思路见https://www.bilibili.com/video/BV13g41157hK?p=6&vd_source=77d06bb648c4cce91c6939baa0595bcd P7 前半部分
//返回入环节点的不考虑额外空间复杂度算法
ListNode* detectCycle(ListNode* head)
{
unordered_set<ListNode*> nodeSet;
ListNode* cur = head;
while (cur != NULL)
{
if (nodeSet.count(cur) != 0)
{
return cur;
}
nodeSet.insert(cur);
cur = cur->next;
}
return NULL;
}
//返回入环节点额外空间复杂度O(1)的算法
ListNode* detectCycle(ListNode* head)
{
ListNode* F = head;
ListNode* S = head;
while (F != NULL)
{
S = S->next;
if (F->next == NULL)
{
return NULL;
}
F = F->next->next;
if (F == S)
{
F = head;
while (F != S)
{
F = F->next;
S = S->next;
}
return F;
}
}
return NULL;
}
//解题完整代码
ListNode* noLoop(ListNode* head1, ListNode* head2);
ListNode* bothLoop(ListNode* head1, ListNode* loop1, ListNode* head2, ListNode* loop2);
ListNode* firstIntersectionNode(ListNode* head1, ListNode* head2)
{
ListNode* res1 = detectCycle(head1);
ListNode* res2 = detectCycle(head2);
if ((res1 == NULL && res2 != NULL) || (res2 == NULL && res1 != NULL))
{
return NULL;
}
else if (res1 != NULL && res2 != NULL)
{
return noLoop(head1, head2);
}
else
{
return bothLoop(head1, res1, head2, res2);
}
}
ListNode* noLoop(ListNode* head1, ListNode* head2)
{
if (head1 == NULL || head2 == NULL)
{
return NULL;
}
ListNode* cur1 = head1;
ListNode* cur2 = head2;
int length = 0;
while (cur1->next != NULL)
{
cur1 = cur1->next;
length++;
}
while (cur2->next != NULL)
{
cur2 = cur2->next;
length--;
}
if (cur1 != cur2)
{
return NULL;
}
cur1 = length > 0 ? head1 : head2;
cur2 = cur1 == head1 ? head2 : head1;
length = abs(length); //求绝对值
for (int i = 0; i < length; i++)
{
cur1 = cur1->next;
}
while (cur1 != cur2)
{
cur1 = cur1->next;
cur2 = cur2->next;
}
return cur1;
}
ListNode* bothLoop(ListNode* head1, ListNode* loop1, ListNode* head2, ListNode* loop2)
{
if (loop1 == loop2)
{
ListNode* cur1 = head1;
ListNode* cur2 = head2;
int length = 0;
while (cur1 != loop1)
{
cur1 = cur1->next;
length++;
}
while (cur2 != loop1)
{
cur2 = cur2->next;
length--;
}
cur1 = length > 0 ? head1 : head2;
cur2 = cur1 == head1 ? head2 : head1;
length = abs(length); //求绝对值
for (int i = 0; i < length; i++)
{
cur1 = cur1->next;
}
while (cur1 != cur2)
{
cur1 = cur1->next;
cur2 = cur2->next;
}
return cur1;
}
else
{
ListNode* cur = loop1;
while (cur != loop2)
{
cur = cur->next;
if (cur == loop1)
{
return NULL;
}
}
return loop2;
}
}


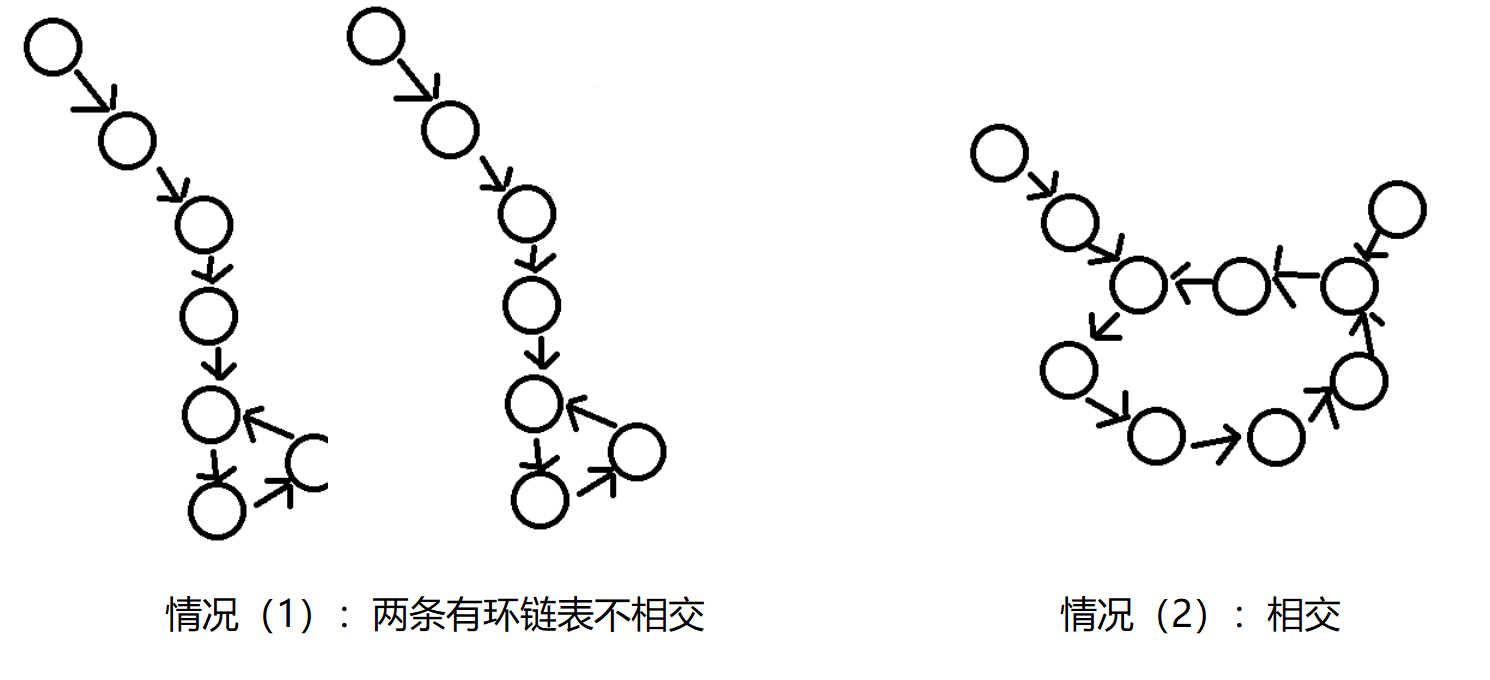 这时从其中一个链表的入环节点loop1继续循环往下遍历,如果loop2相遇了,那么一定是情况(2),此时返回loop2即可,因为loop1和loop2都是第一个相交节点。如果转了一圈走回到了loop1还没遇到loop2,那么就是情况(1),返回NULL
这时从其中一个链表的入环节点loop1继续循环往下遍历,如果loop2相遇了,那么一定是情况(2),此时返回loop2即可,因为loop1和loop2都是第一个相交节点。如果转了一圈走回到了loop1还没遇到loop2,那么就是情况(1),返回NULL
 浙公网安备 33010602011771号
浙公网安备 33010602011771号