Something FUN!!! (geometry)

Let $r_1$ and $r_2$ be the radius of two concenter circles with $r_1<r_2$.

Point $A$ is moving at constant speed on the circle with radius $r_2$, and point $B$ is moving at constant speed on the circle with radius $r_1$.

The midpoint of line $AB$ makes some interesting diagrams.

For example, if $r_2=2r_1$, the resulting shape is a cardioid.

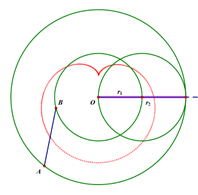
If $r_2=3r_1$, there is something like Garfield’s eyes.

  

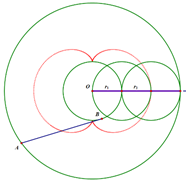
For $r_2=4r_1$, the shape is reminiscent of a nice clover.

 

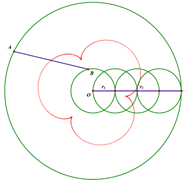
When $r_2=6r_1$, there is a blooming Catharanthus roseus.

 

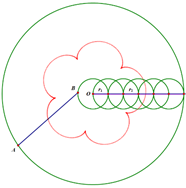
In general, for $r_2=kr_1$, the “flower” has $(k-1)$ “petals”.