线索二叉树,树和森林

线索二叉树,树和森林

线索二叉树

为什么要研究线索二叉树?

二叉链表存储的二叉树无法找到某个结点的在某种遍历序列里面的前驱和后继结点.

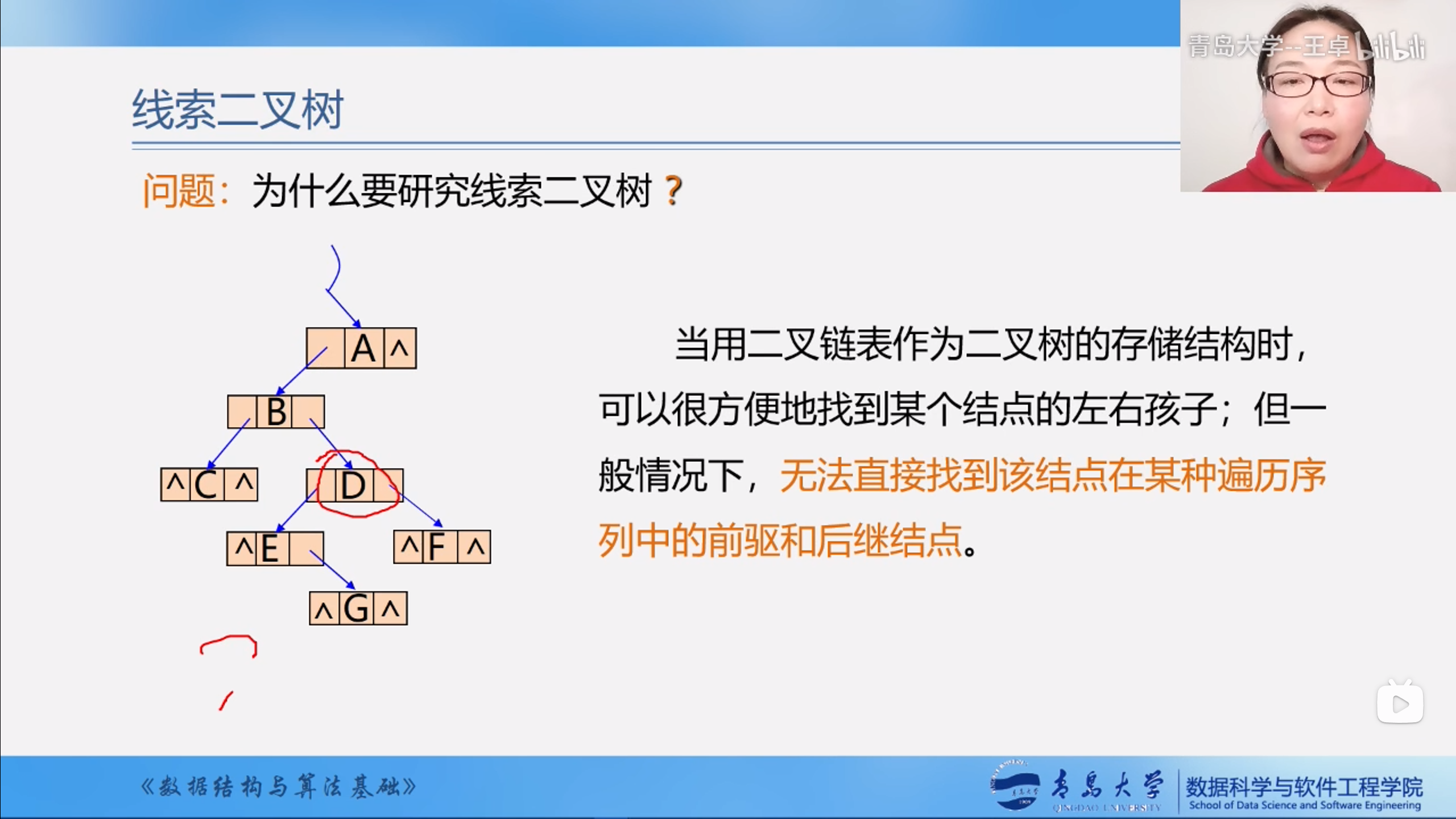
我们利用二叉链表中的指针与来寻找特定遍历序列的二叉树结点的前驱和后继

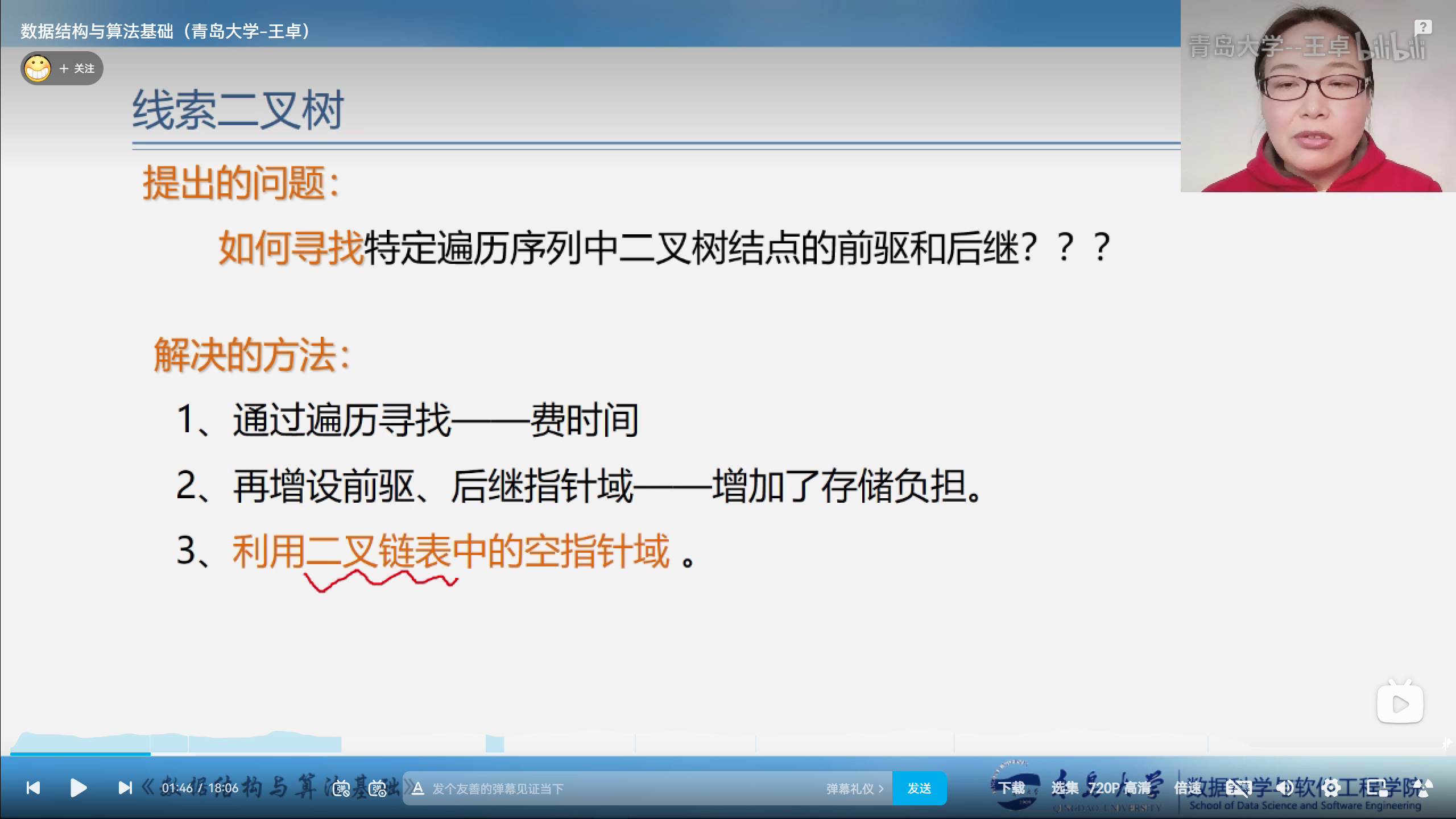
根据前面的所学的内容,二叉链表中有n+1个空指针域,我们要把这些空指针域来利用起来.

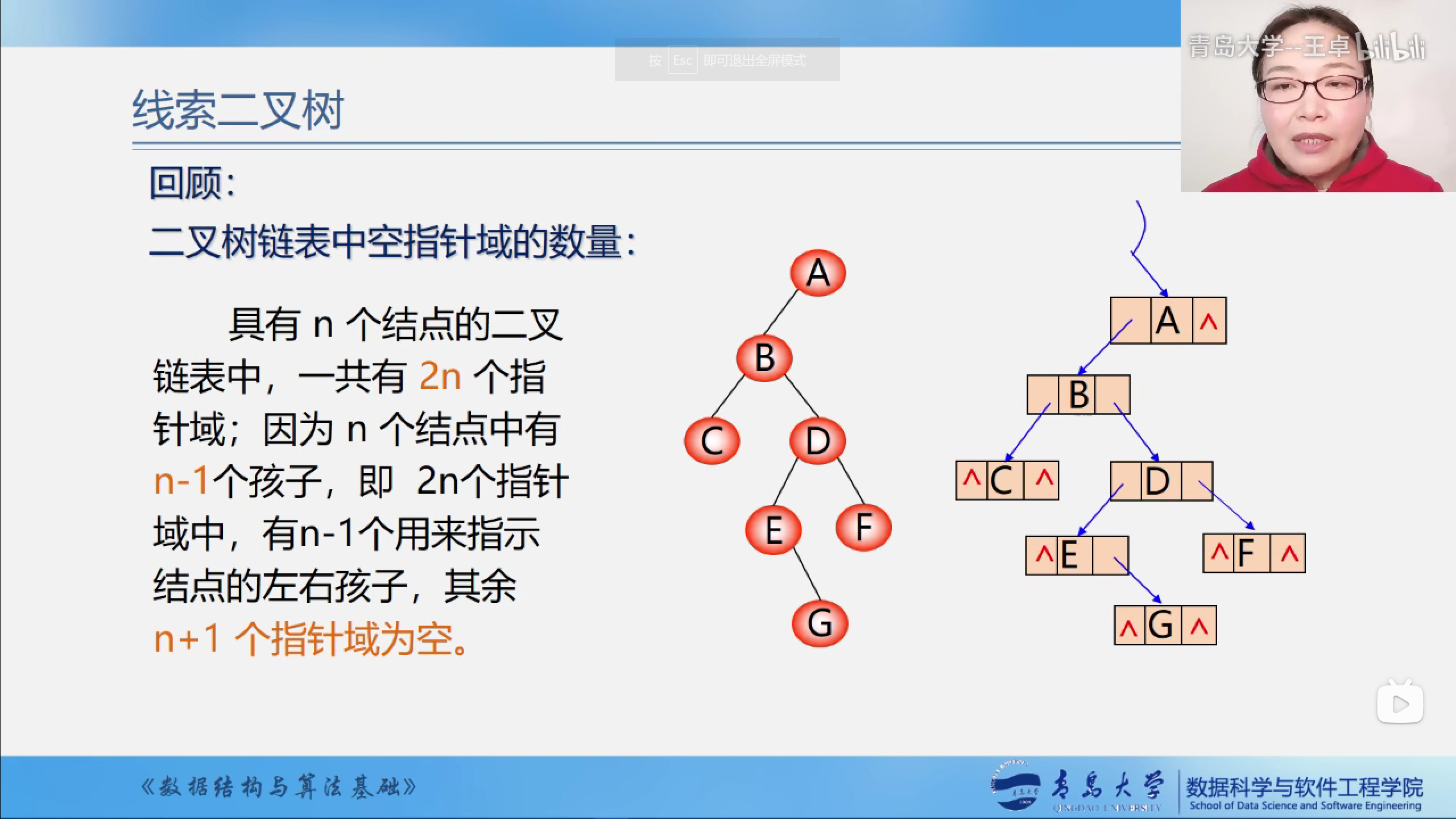
线索二叉树

如果某个结点的左孩子为空,则将左孩子的指针域改为指向其前驱.

如果某个结点的右孩子为空,则将右孩子的指针域改为指向其后继.

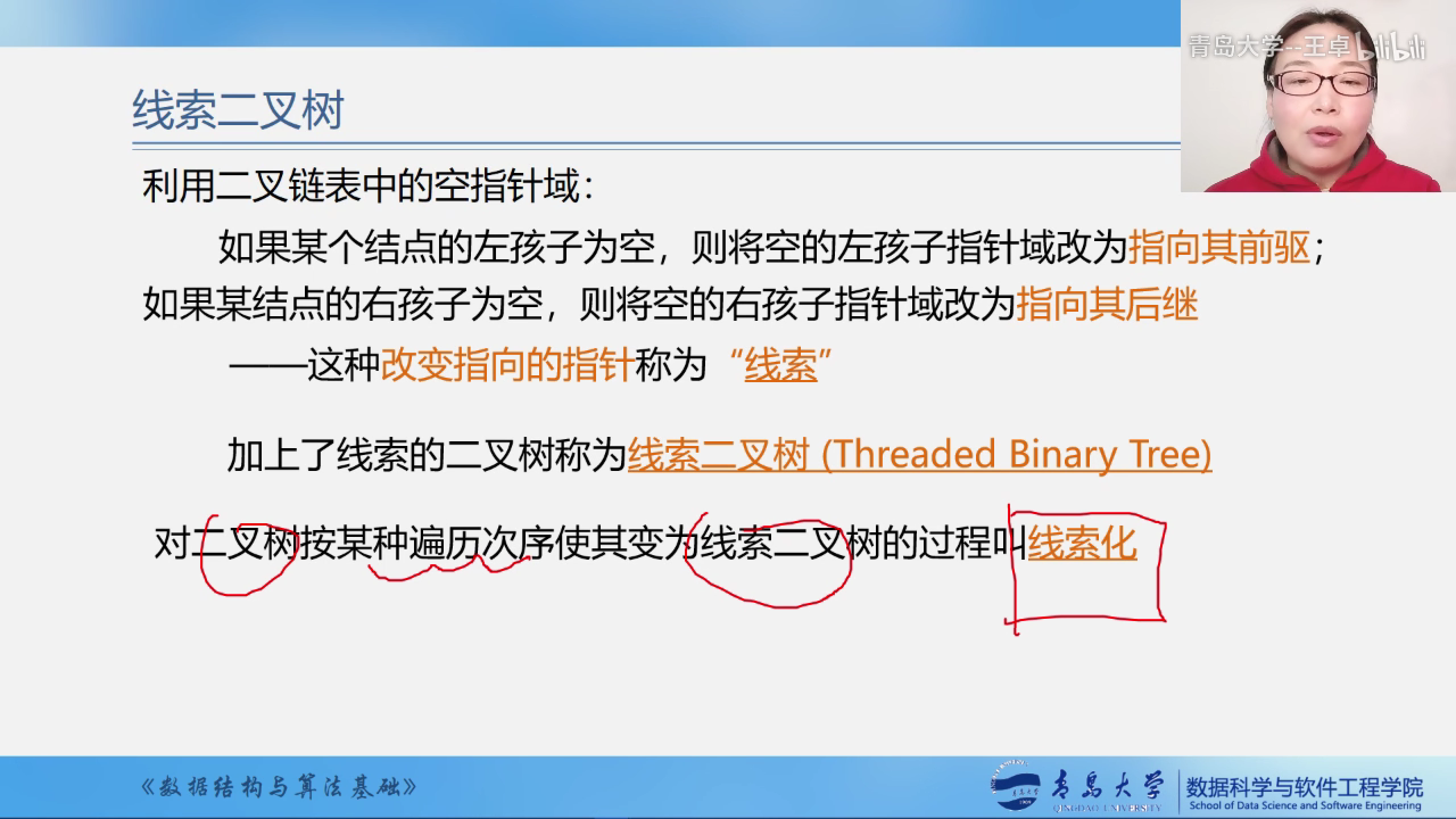
注意不是指向其双亲结点,而是指向其在某中遍历顺序下的前驱和后继结点.

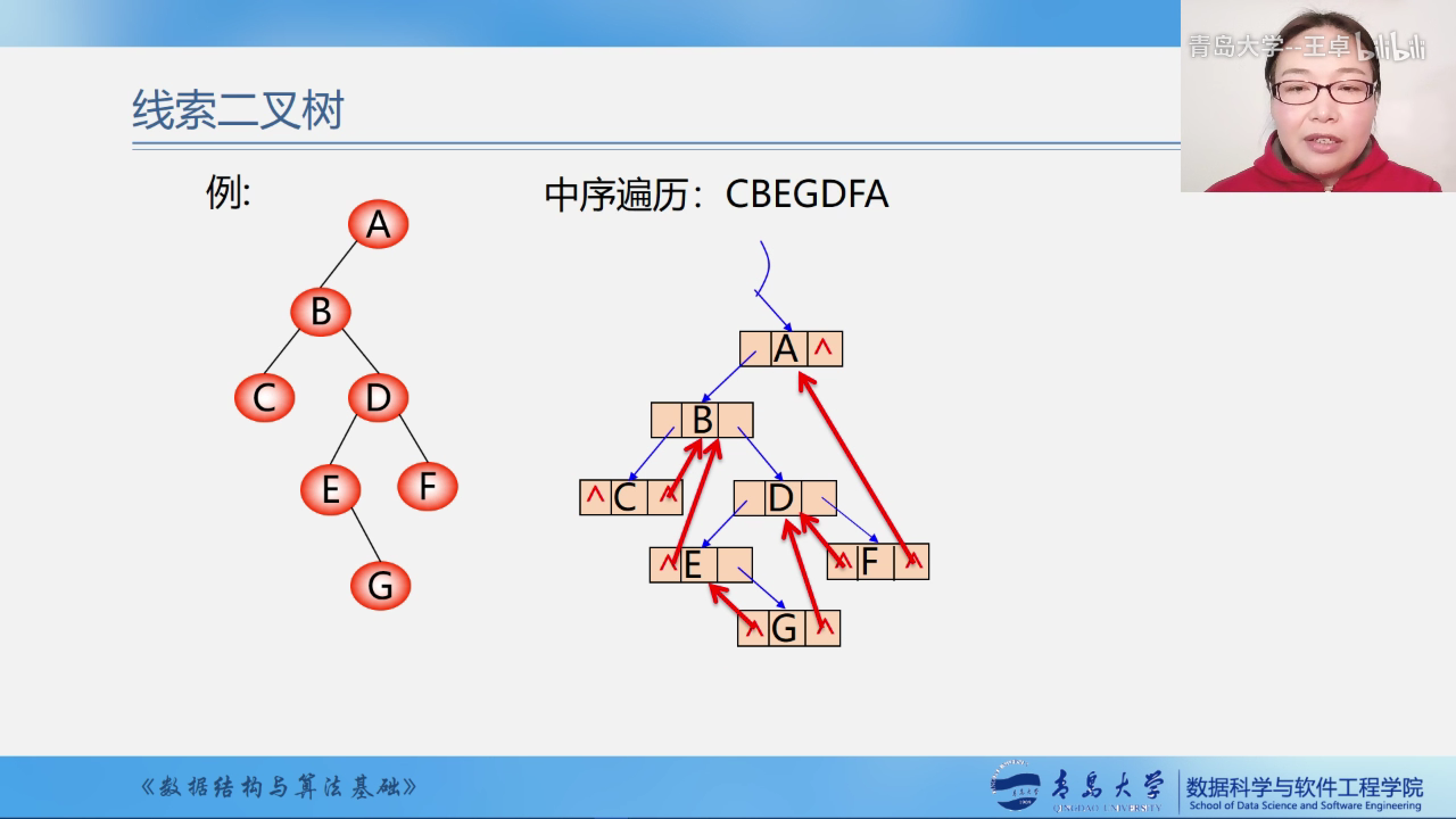
但是增设了这些指针之后,会难以区分是指向孩子的指针还是指向前驱结点或者后继结点的指针,因为指针是一个地址是无法区分出来的.

解决办法是加上两个标志域ltag和rtag

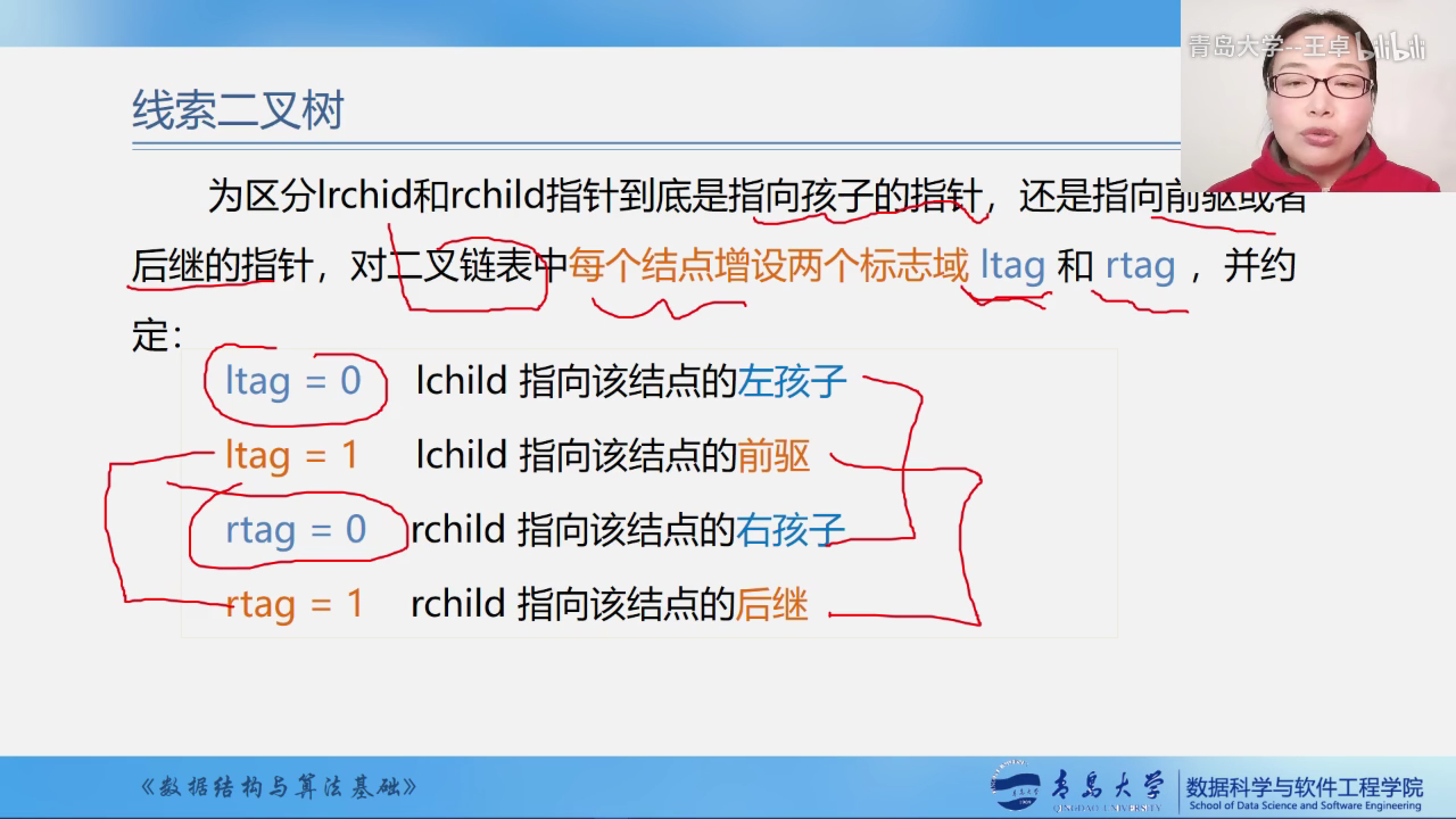
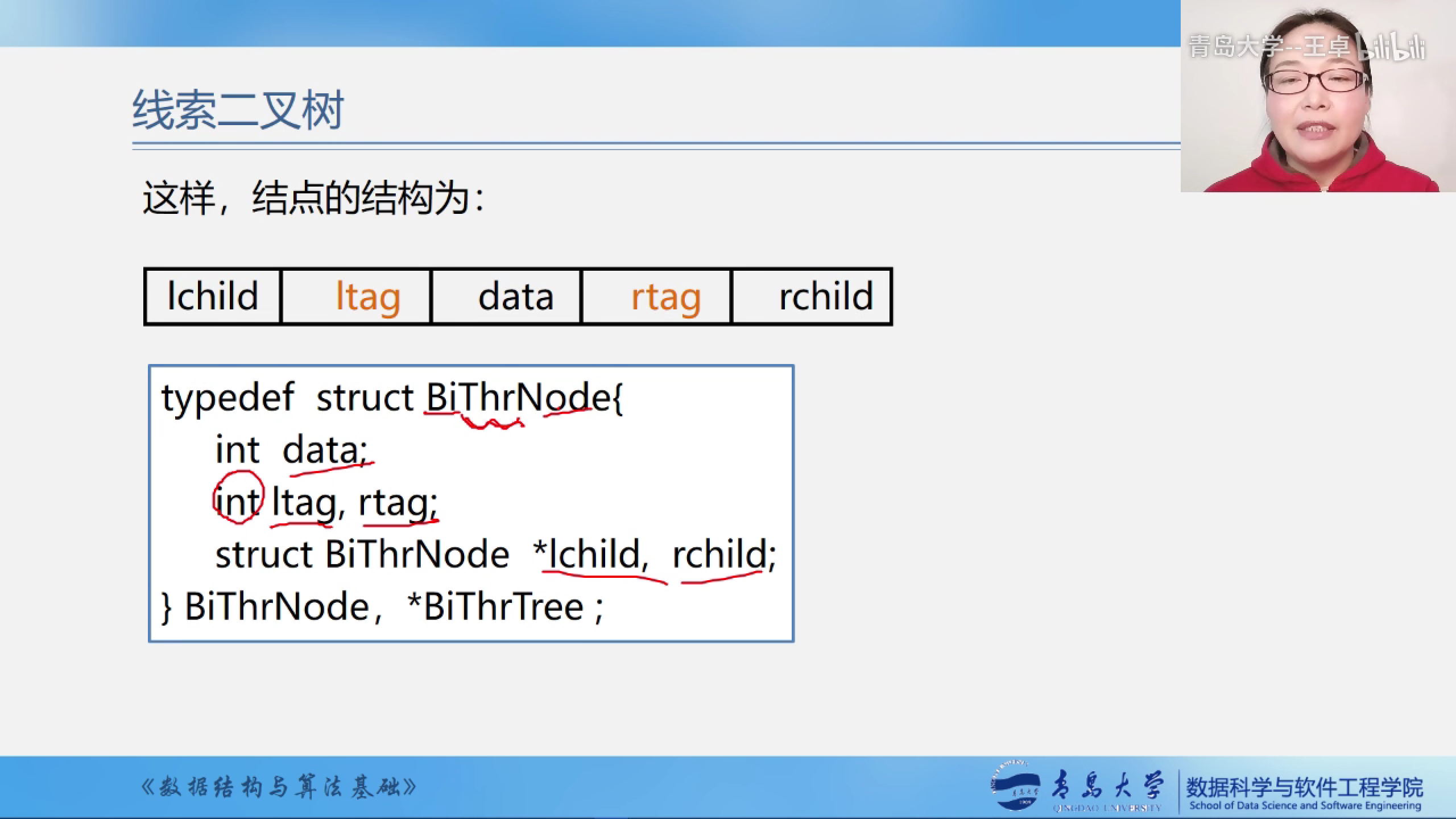
线索二叉树的结点结构有5部分构成

分别是

指向左右孩子的指针lchild,rchild

数据域

两个标志域,ltag和rtag

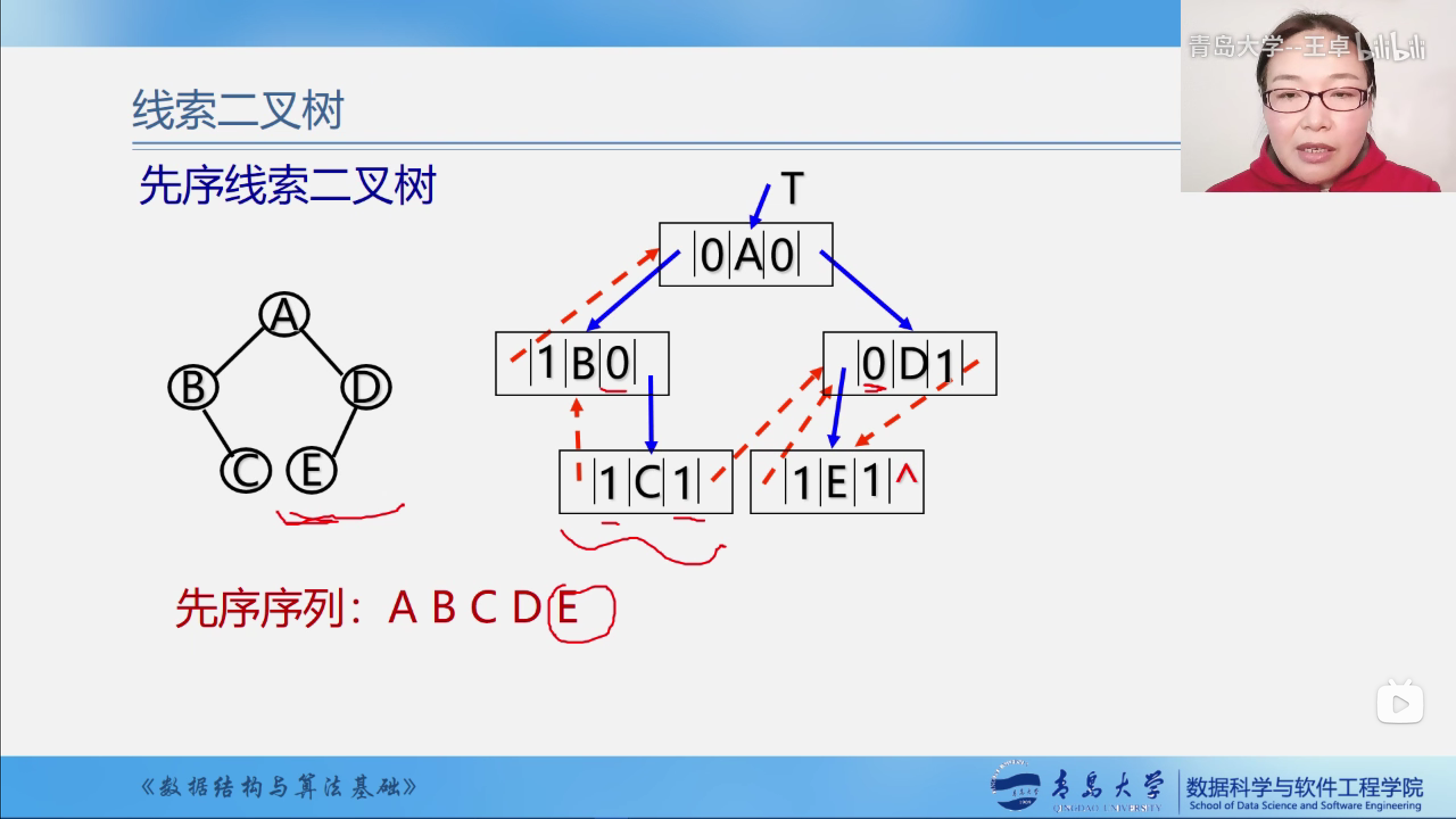
先序线索二叉树

中序线索二叉树

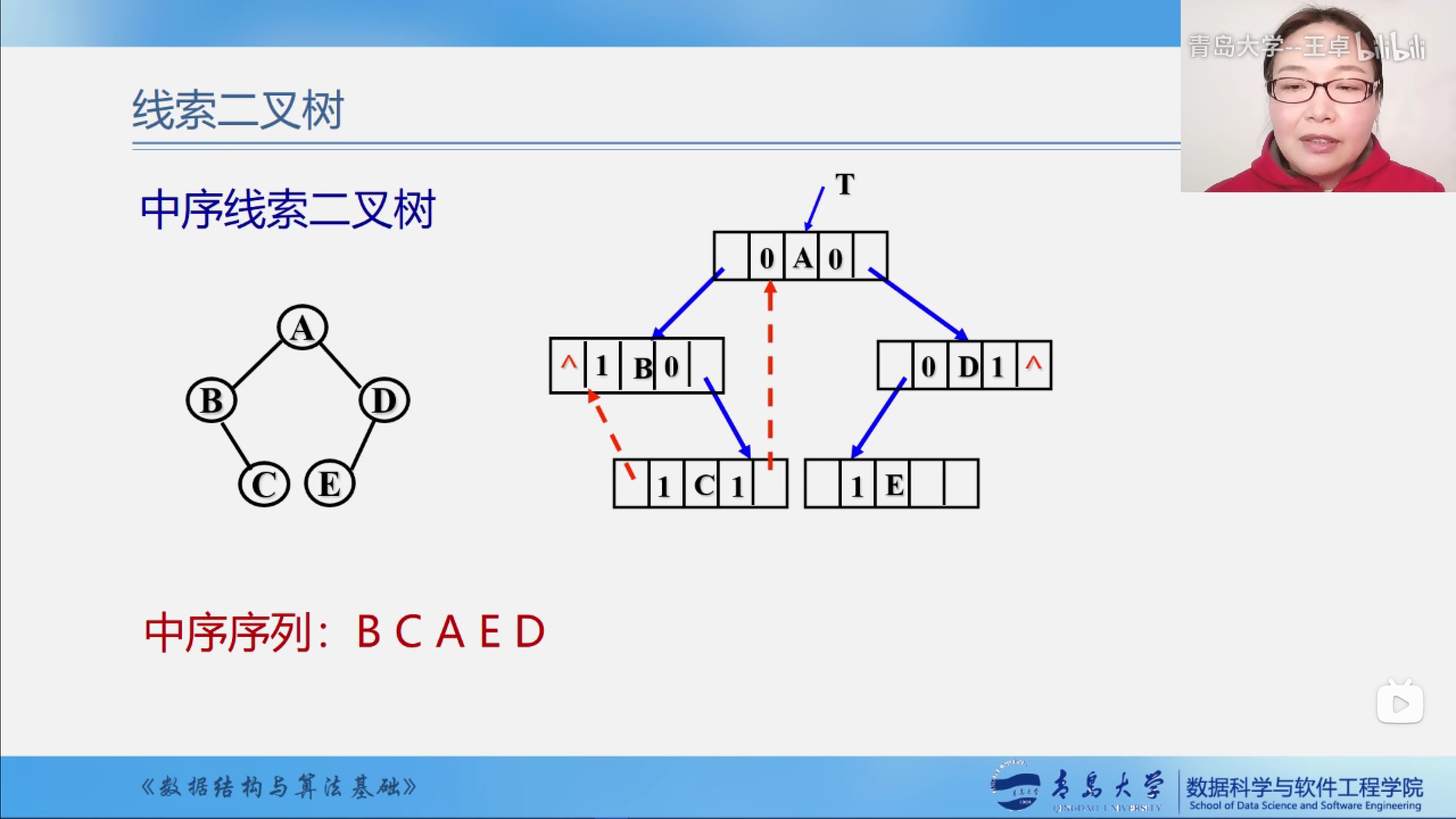
后序线索二叉树

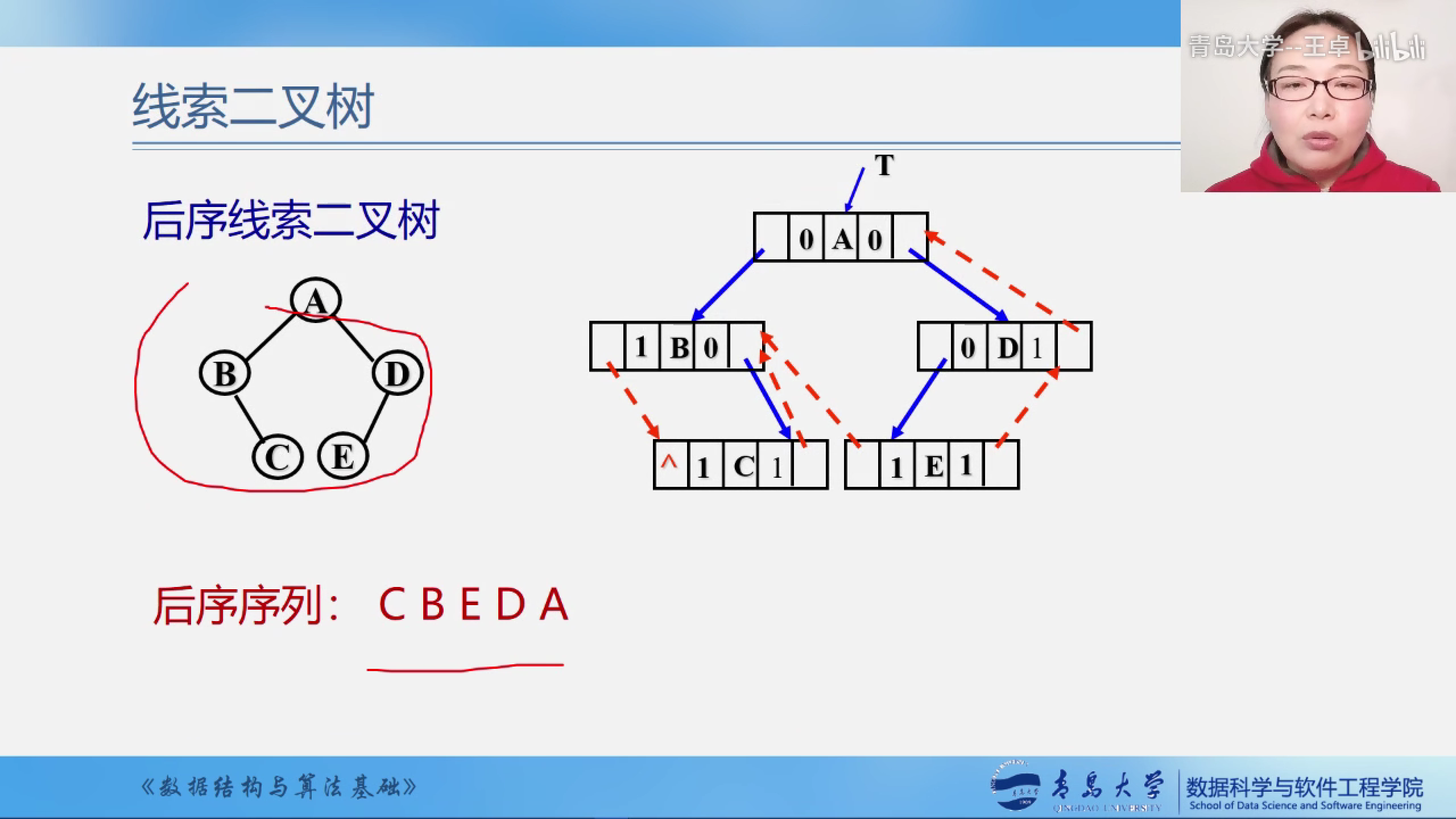
练习

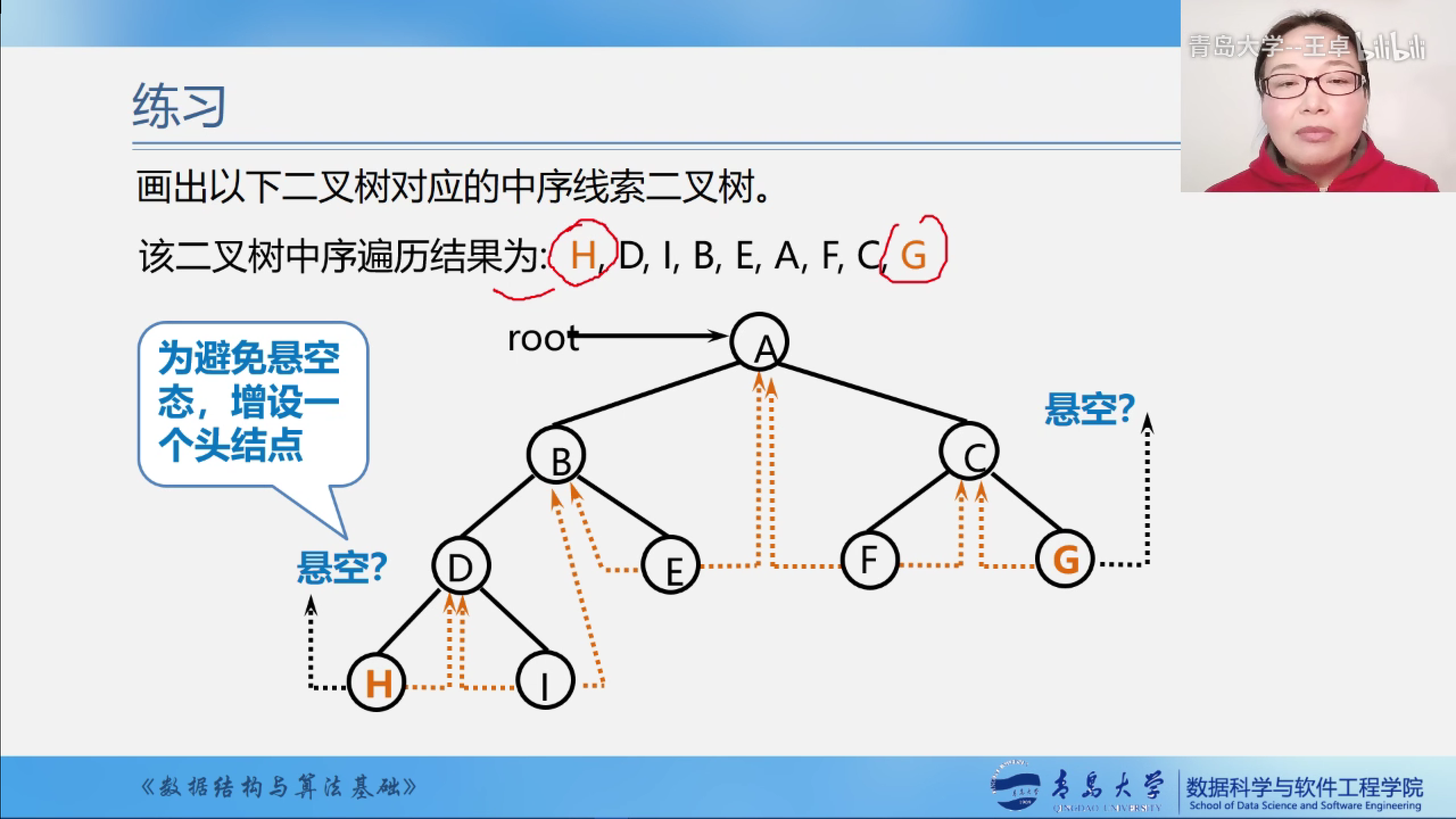
线索二叉树还是有指针会悬空,(即空指针域,因为在某种遍历序列当中某个结点可能没有前驱和后继)怎么解决?

可以增加一个头结点

让头结点的左指针指向根结点,头结点的右指针指向二叉树遍历顺序的最后结点

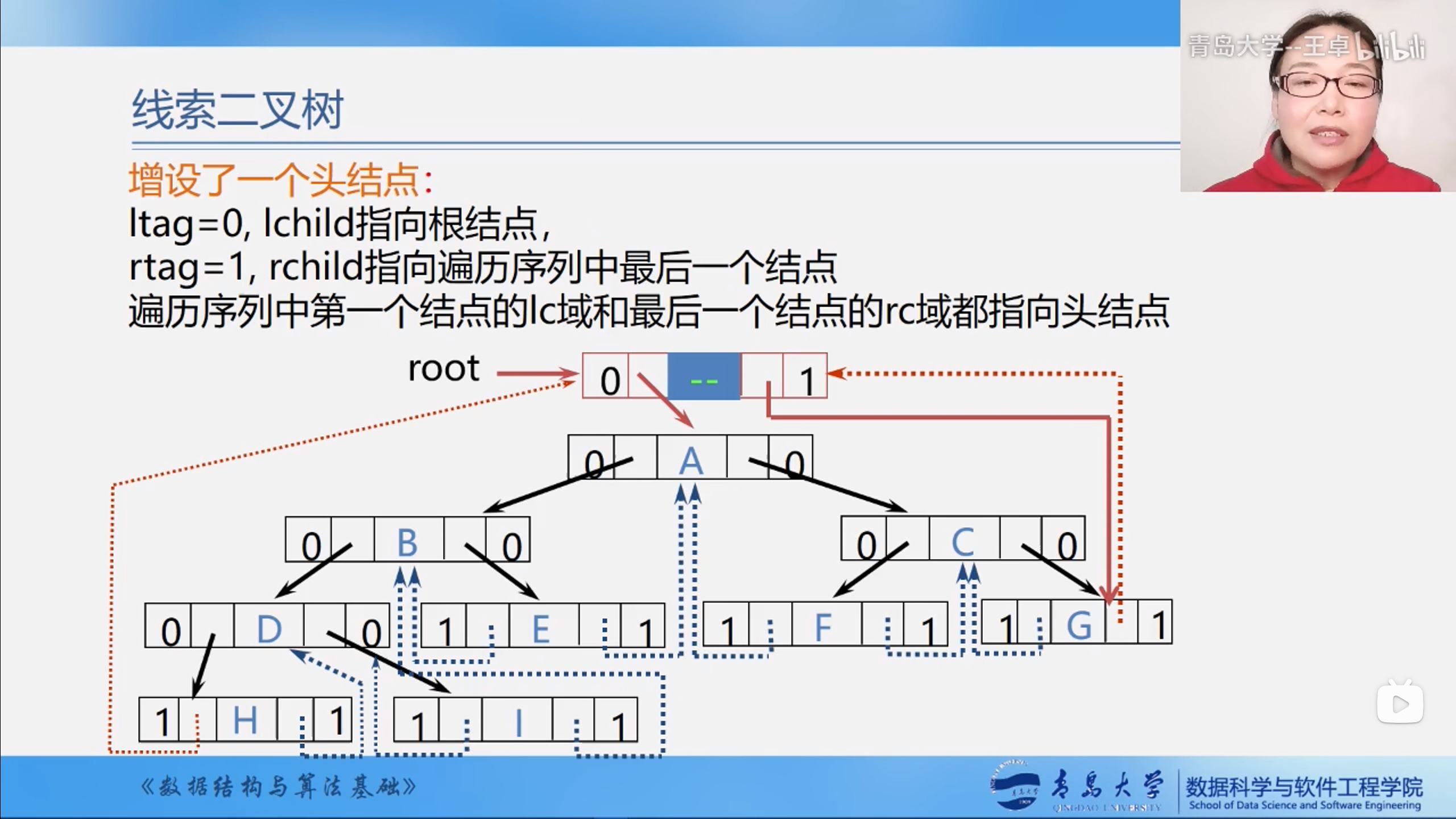
为什么线索二叉树中不能让指针悬空,最后要额外加上一个本来就不存在的头结点呢?

而且为啥这个设置头节点ltag=0,rtag=1?

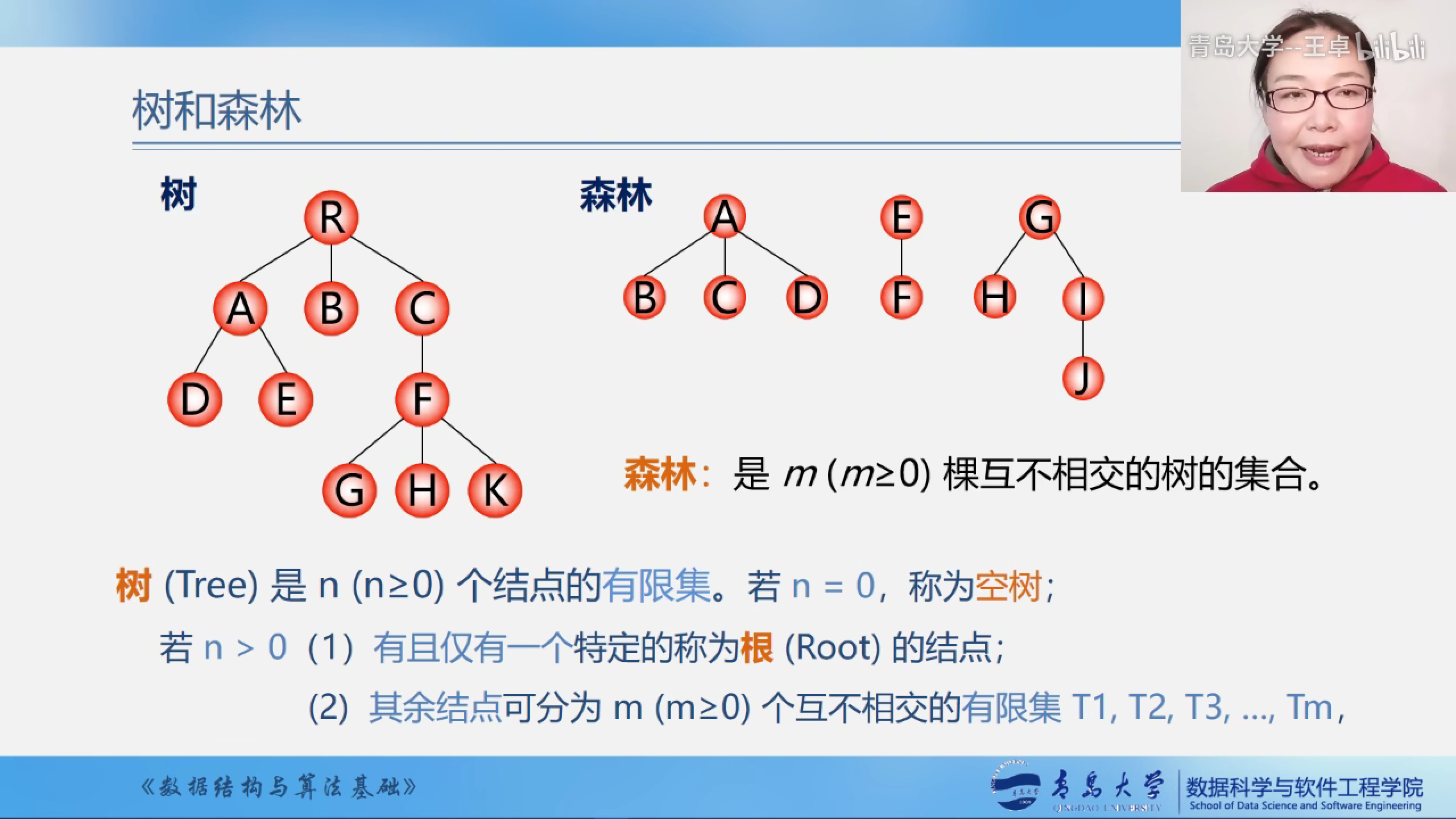
树和森林

森林是m棵互不相交的树的集合.

将树去掉根结点可以变成森林,将森林的每个树全部加上根结点可以变成一颗树.

根据树的定义可以看出,树也是一个递归的定义.

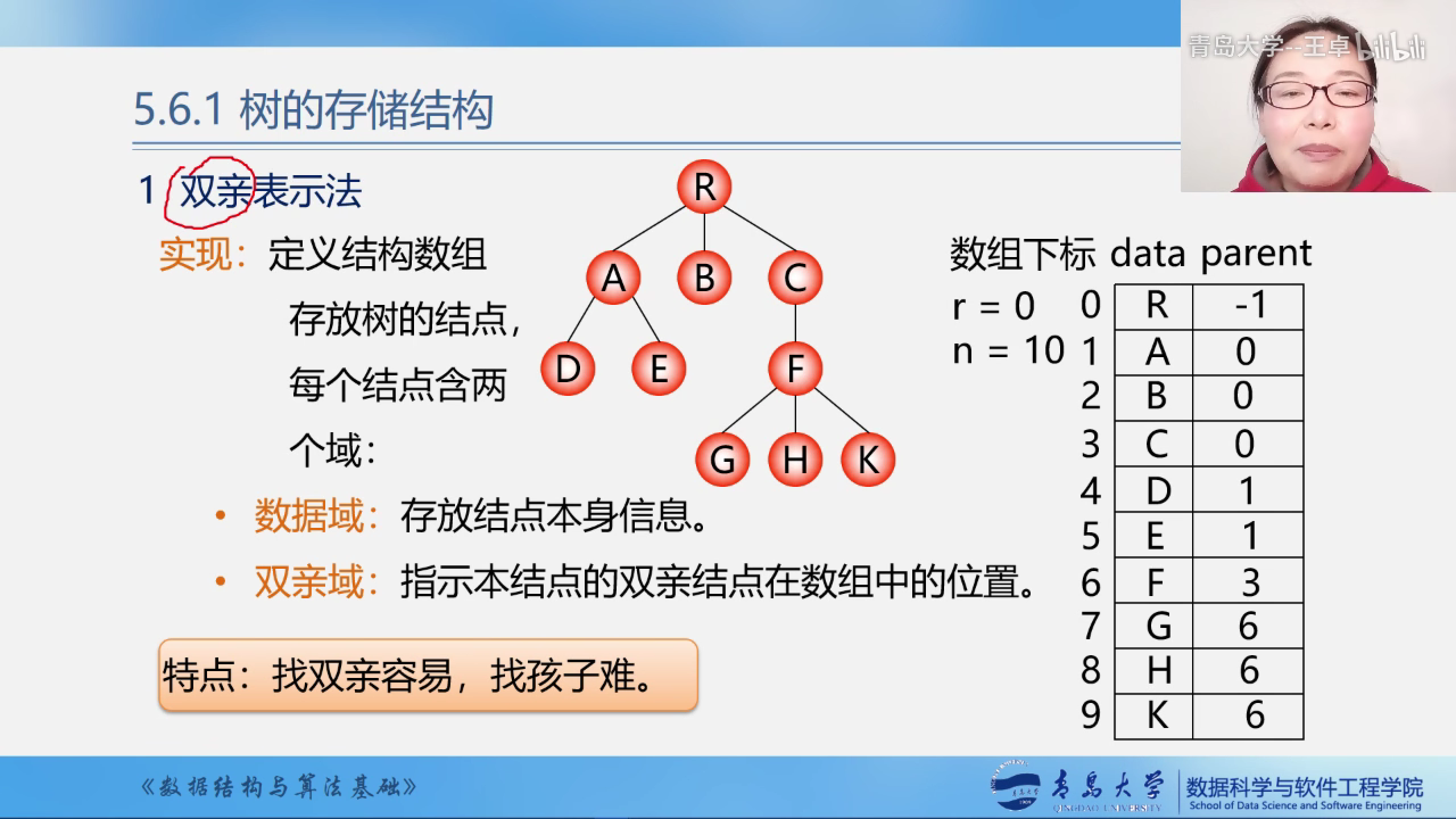
树的存储结构

双亲表示法

数据域:存放结点本身数据

双亲域:存放双亲结点在数组当中的位置.

特点:找双亲容易,找孩子难.

下图的编号是按照层序遍历的方式来编号的.

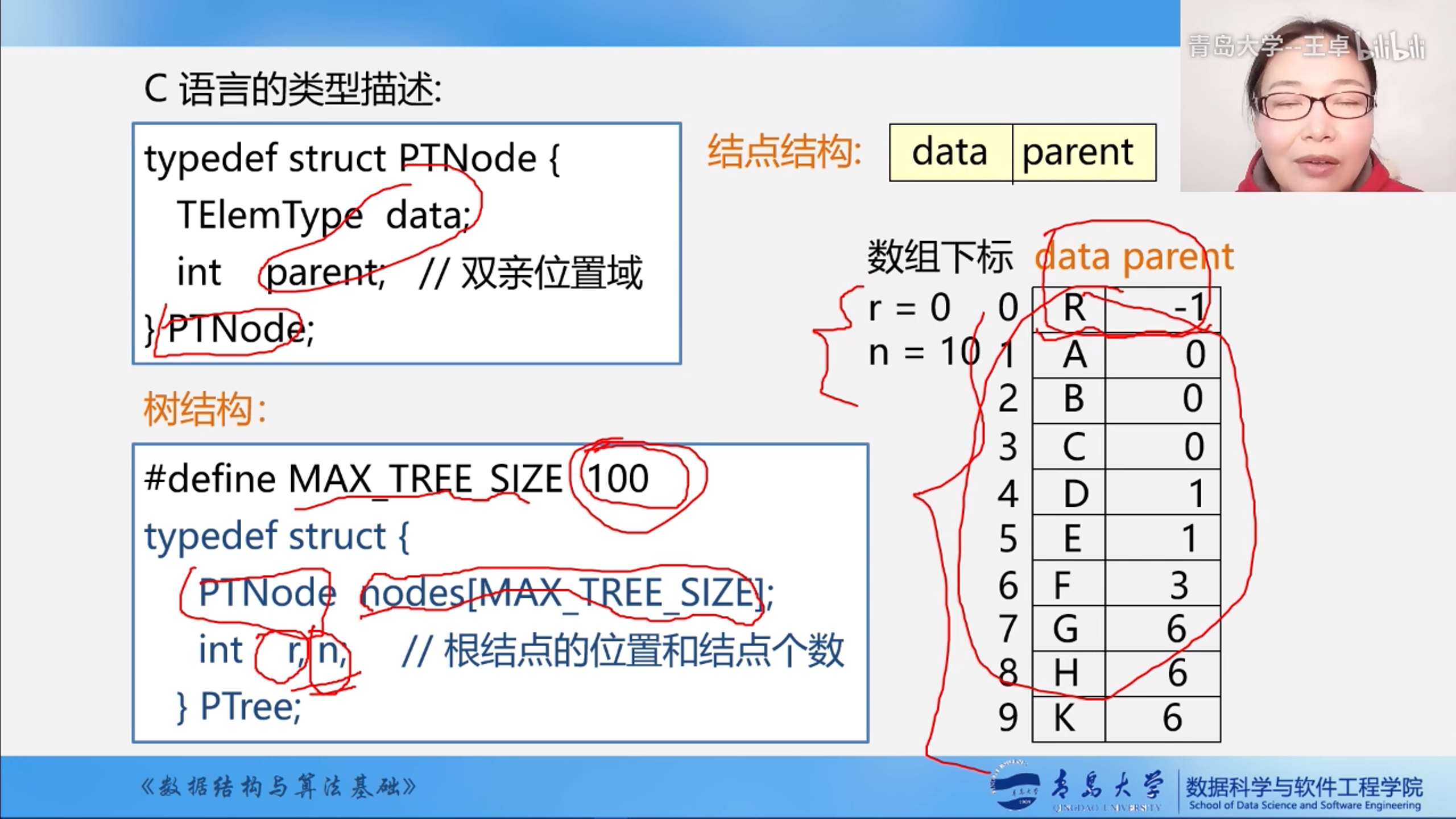
双亲表示法使用结构体数组存储

1. 首先定义结构体结点
2. 然后开辟一个结构体数组来存储数据
3. 

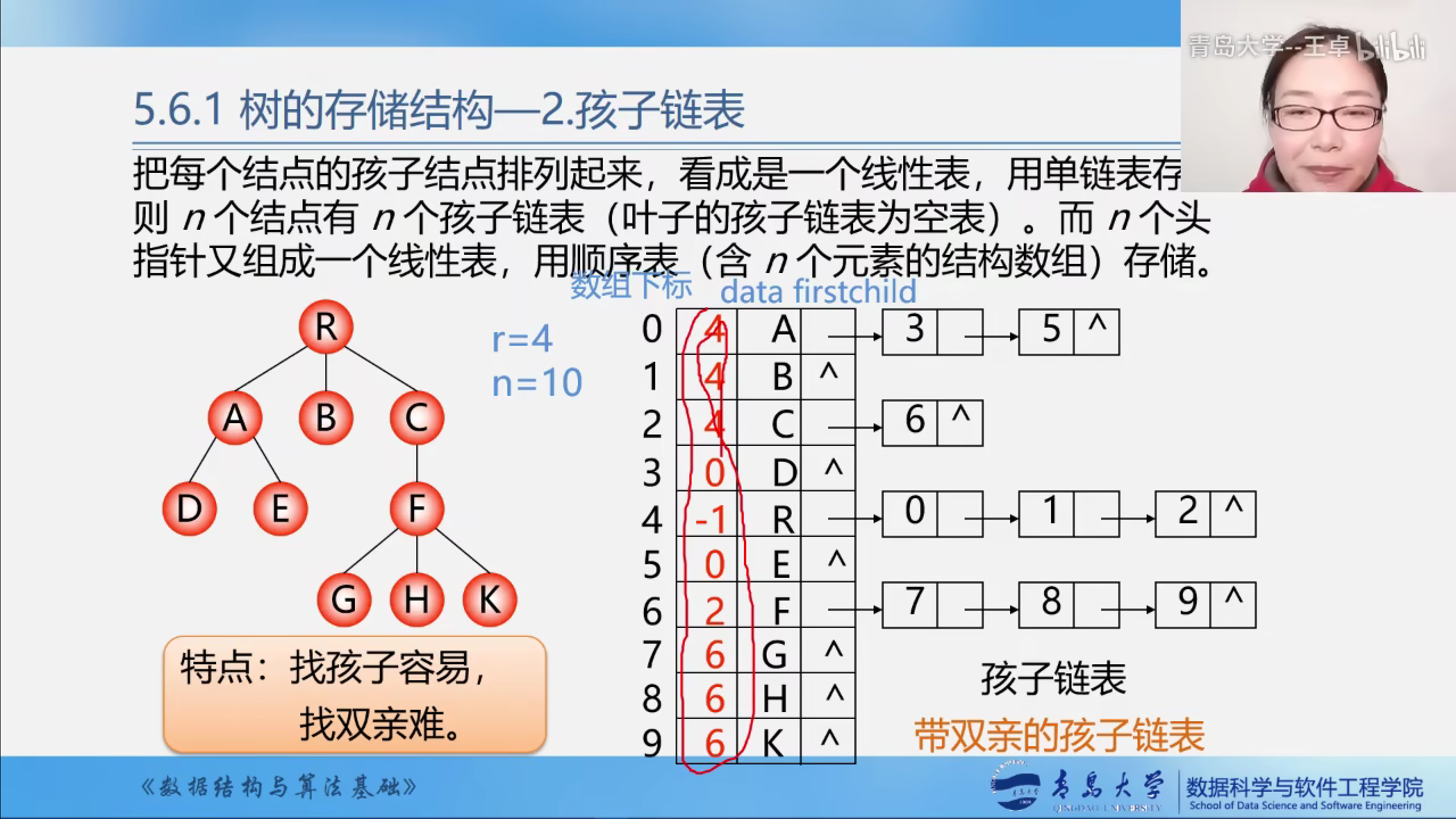
孩子链表存储

1. 将每个结点的孩子用链表存储起来
2. 保存每个链表的头指针
3. 将头指针的数组保存起来,用线性表存储
4. 寻找孩子容易,找双亲难

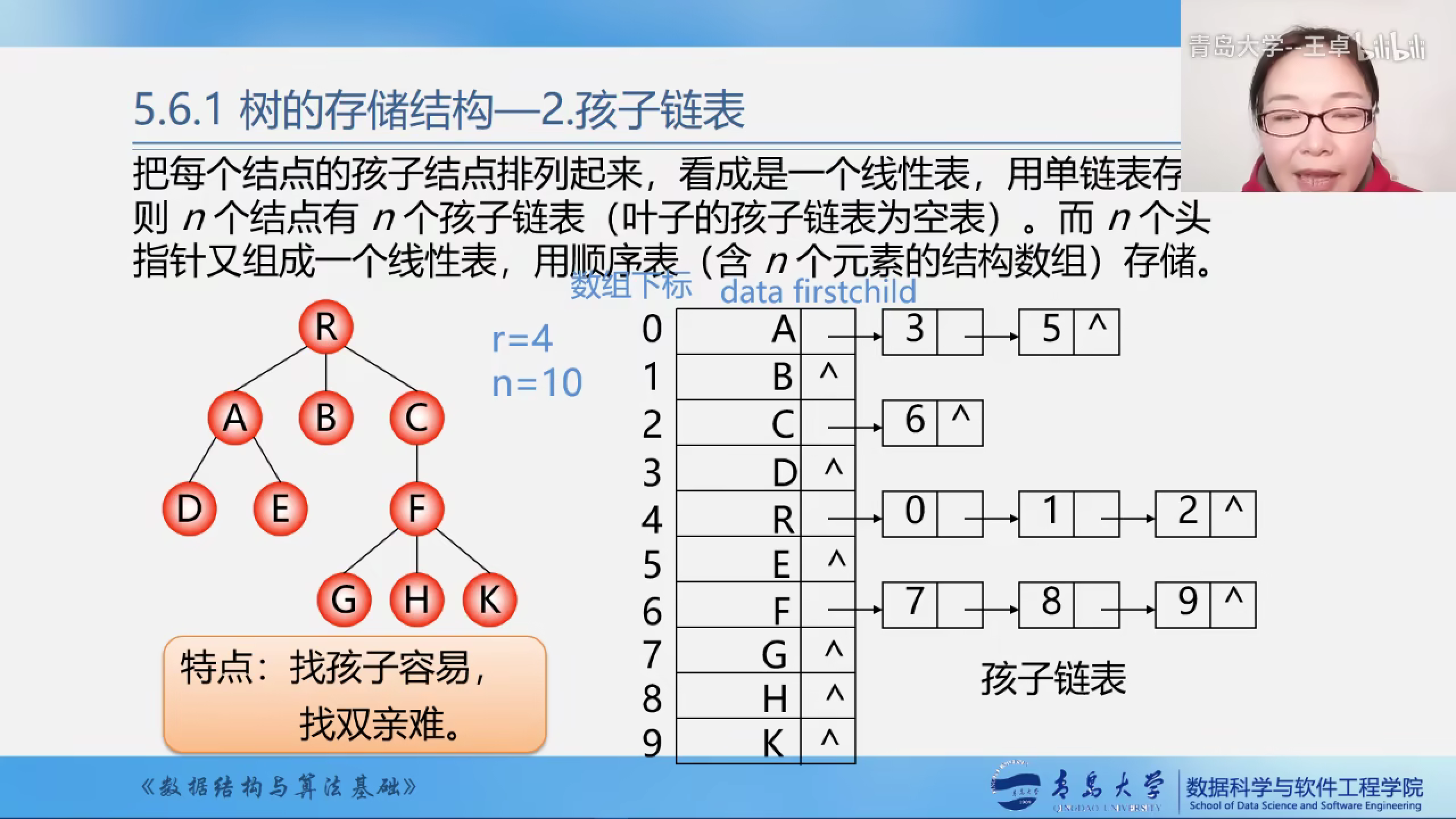
每个结点都是一个头节点,然后指向自己的孩子.

带双亲的孩子链表

可以将上面的双亲表示法和孩子链表表示法合并到一起.

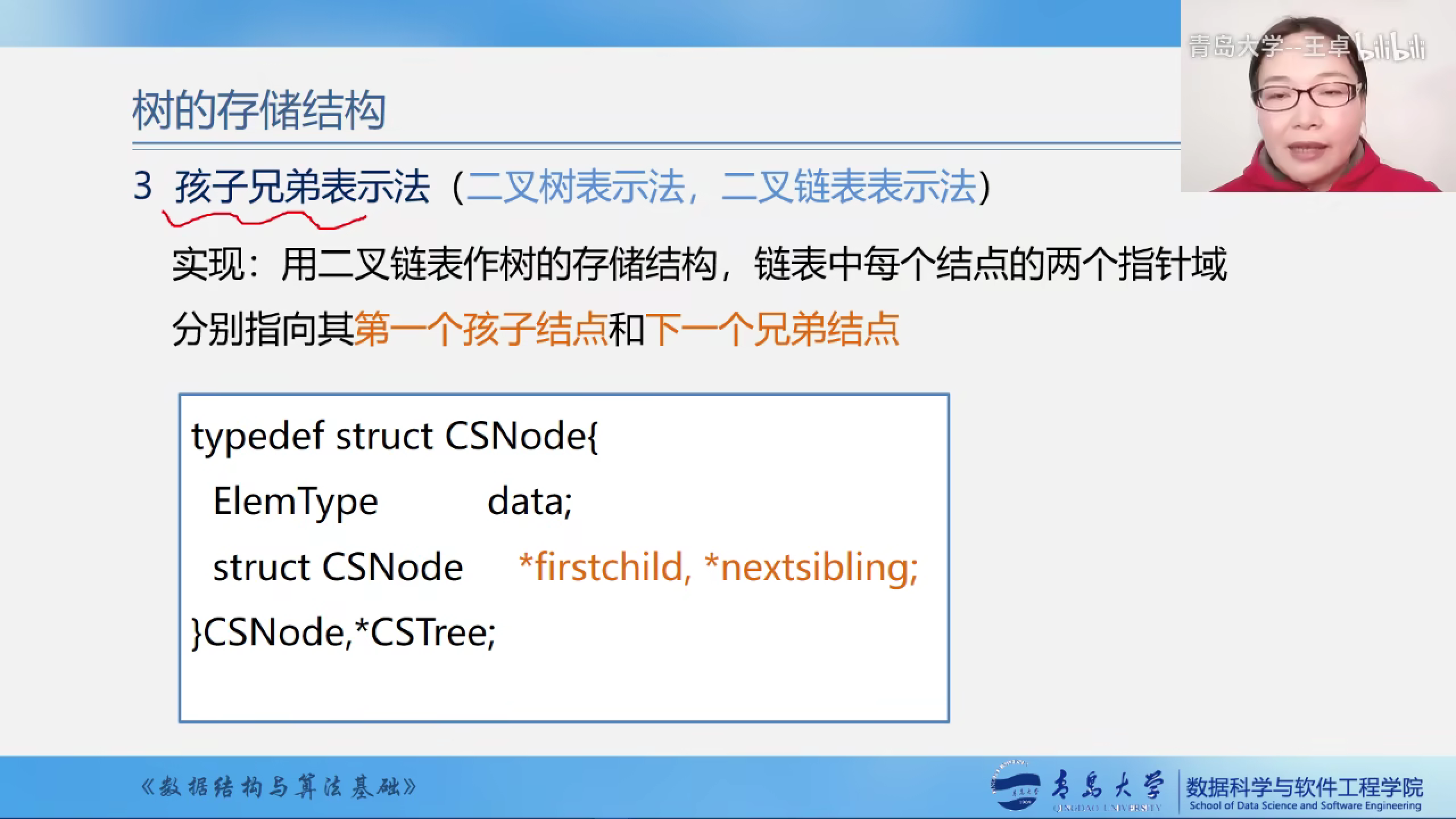
孩子兄弟表示法

使用二叉链表来存储树的结构.

一个指针指向其第一个孩子

一个指针指向其下一个兄弟

通过右指针去寻找兄弟,通过左指针去寻找孩子

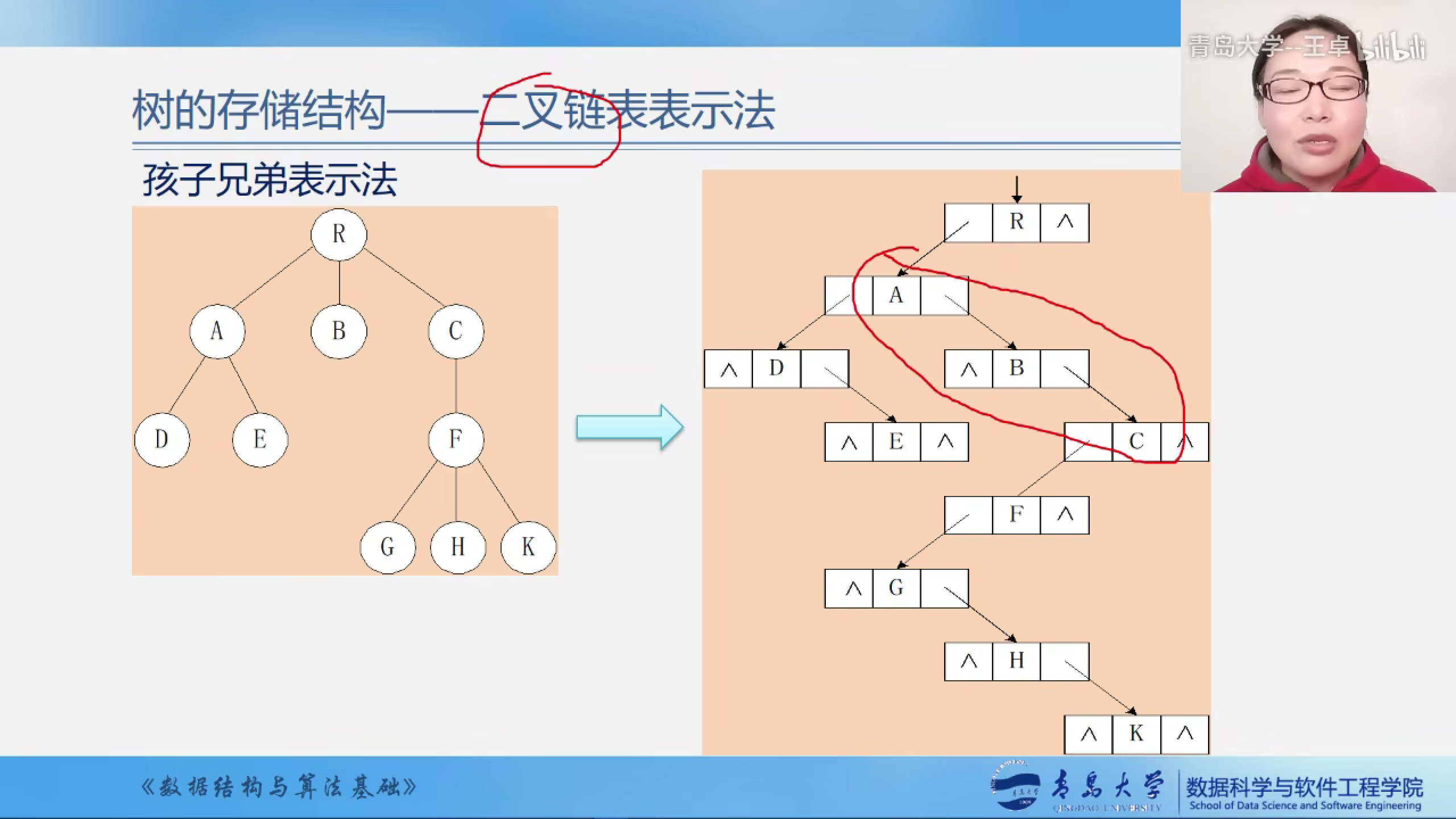
孩子兄弟表示法的具体实现过程演示.

孩子兄弟表示法的好处?

将树可以转换为二叉树,便于存储.

可以通过每次寻找左孩子找到该结点的第一个孩子,然后通过这个孩子的右指针找到这个结点的所有孩子.

树使用二叉链表存储

树和二叉树需要转换

如果树使用用二叉链表来储存的话

该结点的左指针指向该结点的下一个孩子,右指针指向该结点的下一个兄弟.

其实就是一个孩子兄弟链表的形式,通过这样做树就可以表示为一个唯一的二叉树了

注意:二叉树是左指针指向左孩子,右指针指向右孩子.

注意:而树的二叉链表是左指针指向该结点的第一个孩子,右指针指向该结点的下一个兄弟.

这两者之间有唯一的对应关系

给定一颗树,就可以找带唯一的一颗二叉树与之对应.

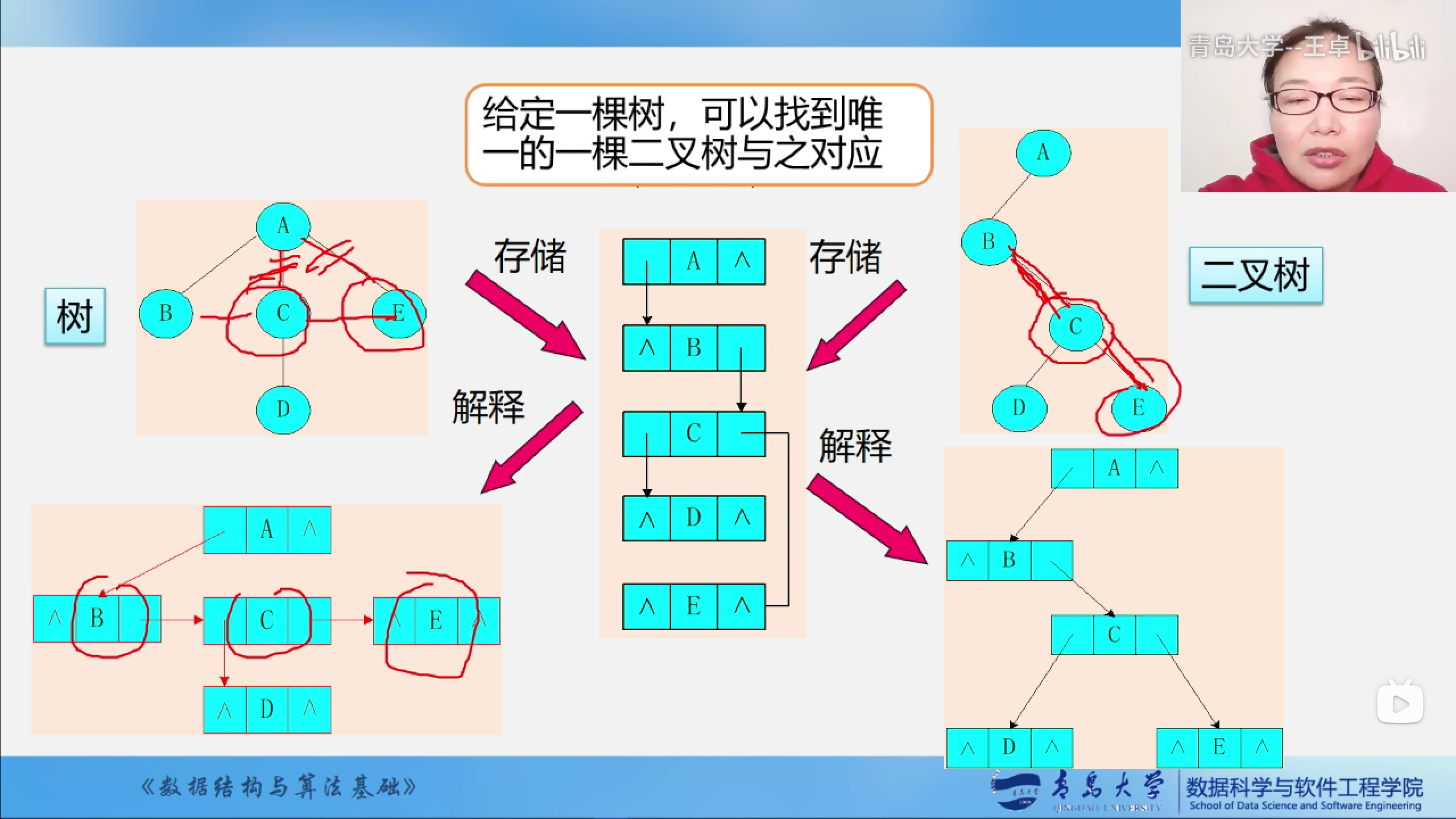
树中的下一个兄弟就是二叉树中的右孩子

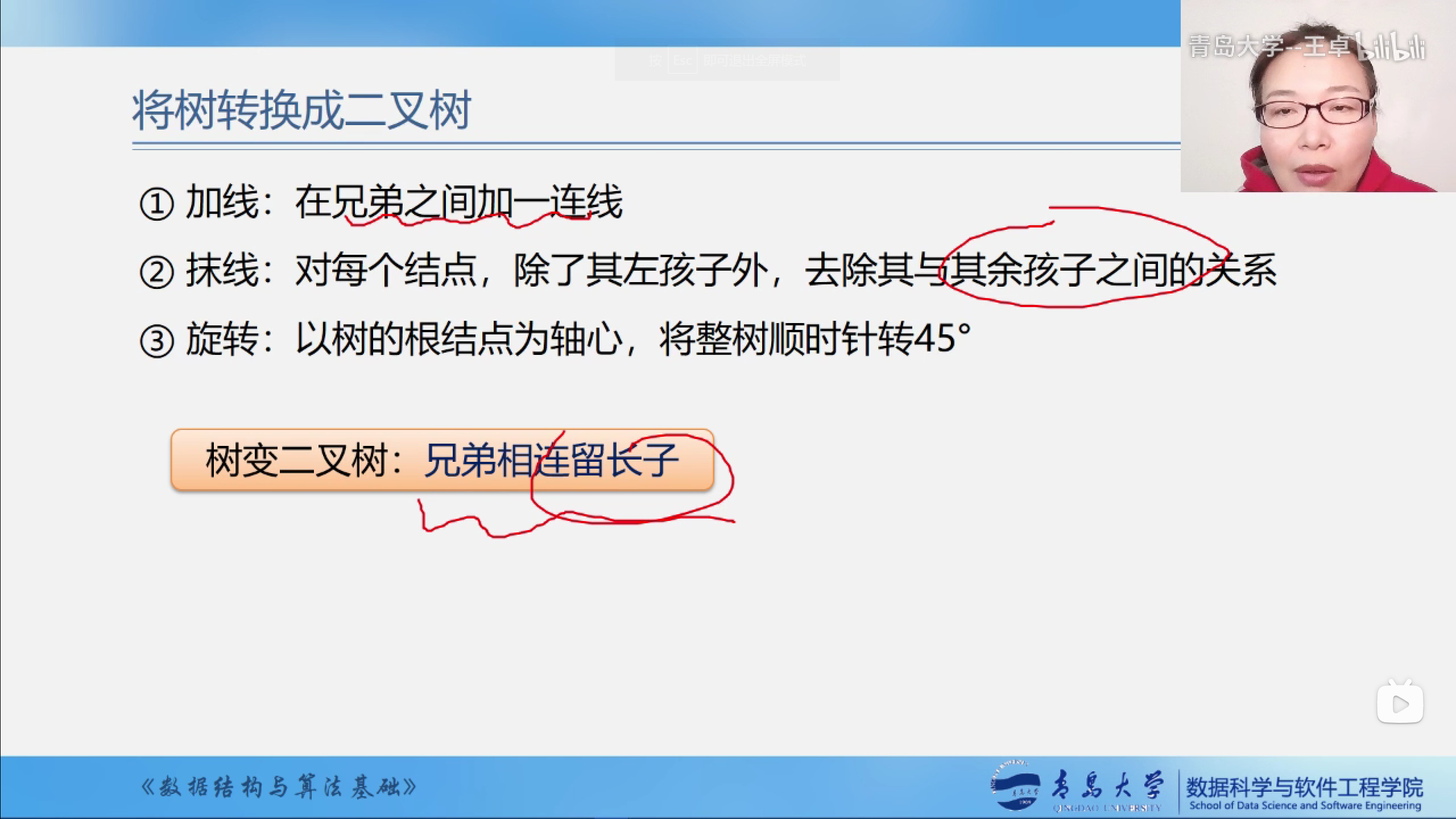
将树转换为二叉树

1. 加线:
2. 抹线:
3. 旋转:

树变二叉树:兄弟相连留长子

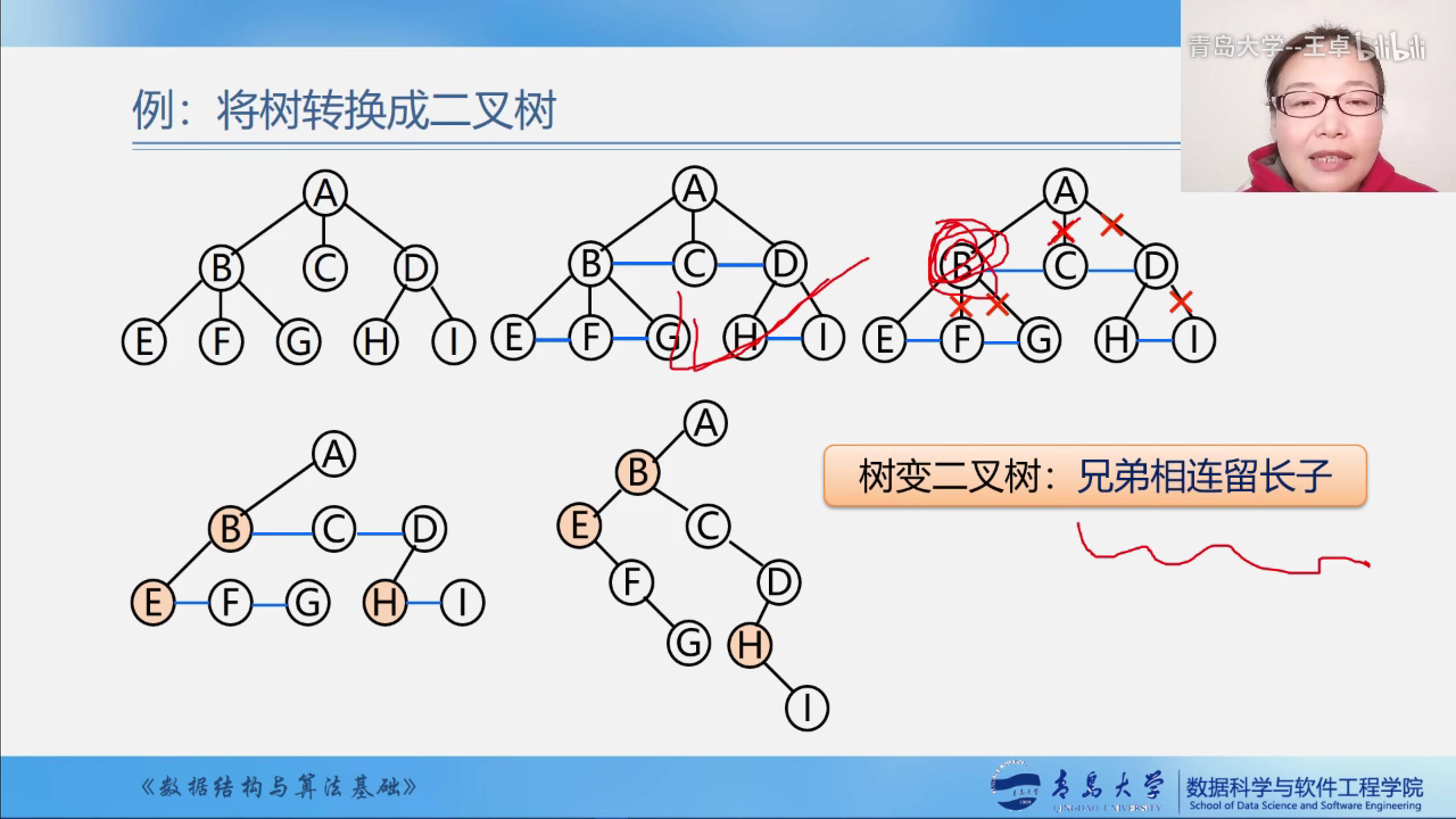
例子:

1. 加线
2. 抹线
3. 旋转

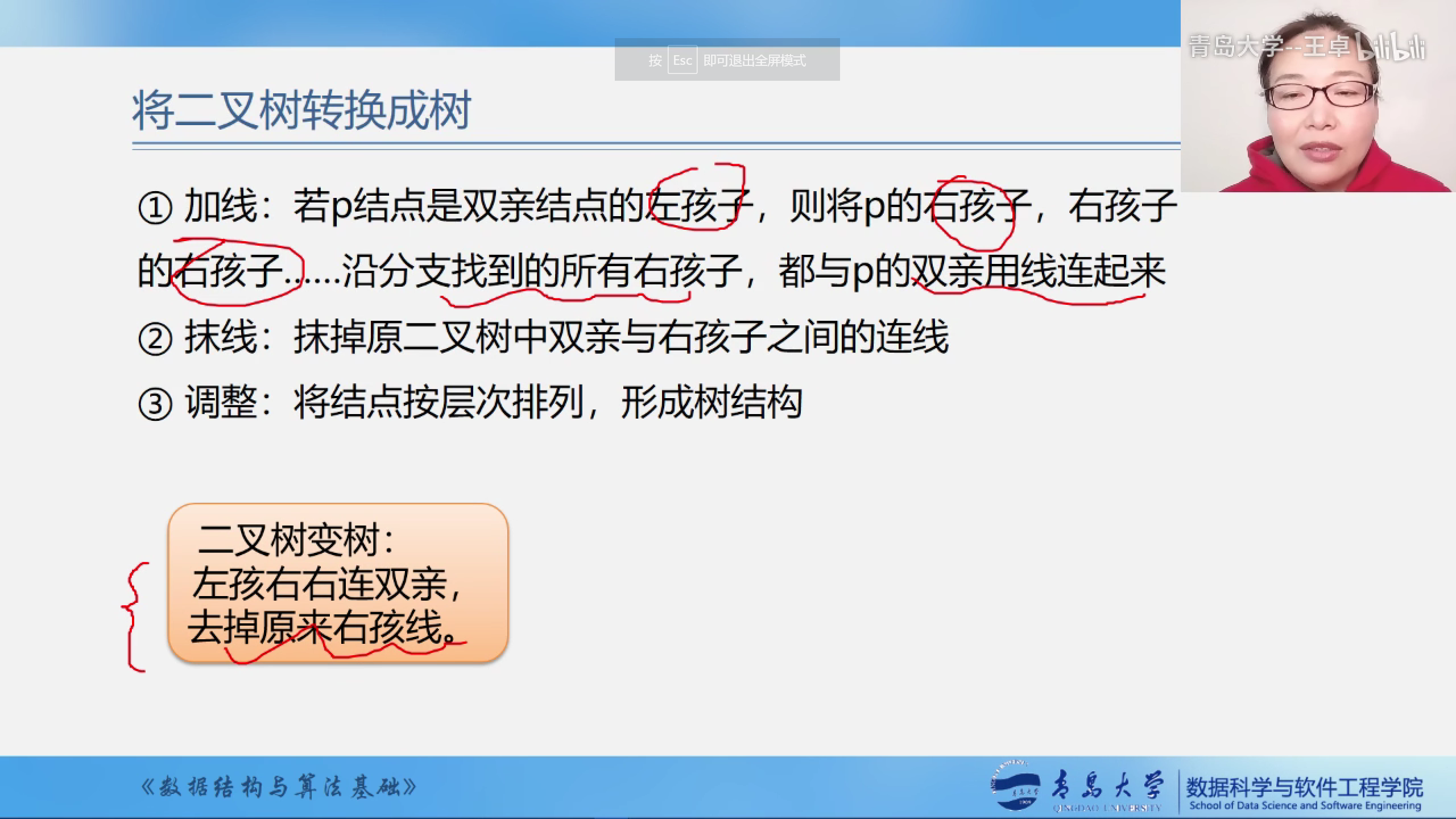
将二叉树转换为树

1. 加线
2. 抹线
3. 调整

左孩右右连双亲

去掉原来右孩线

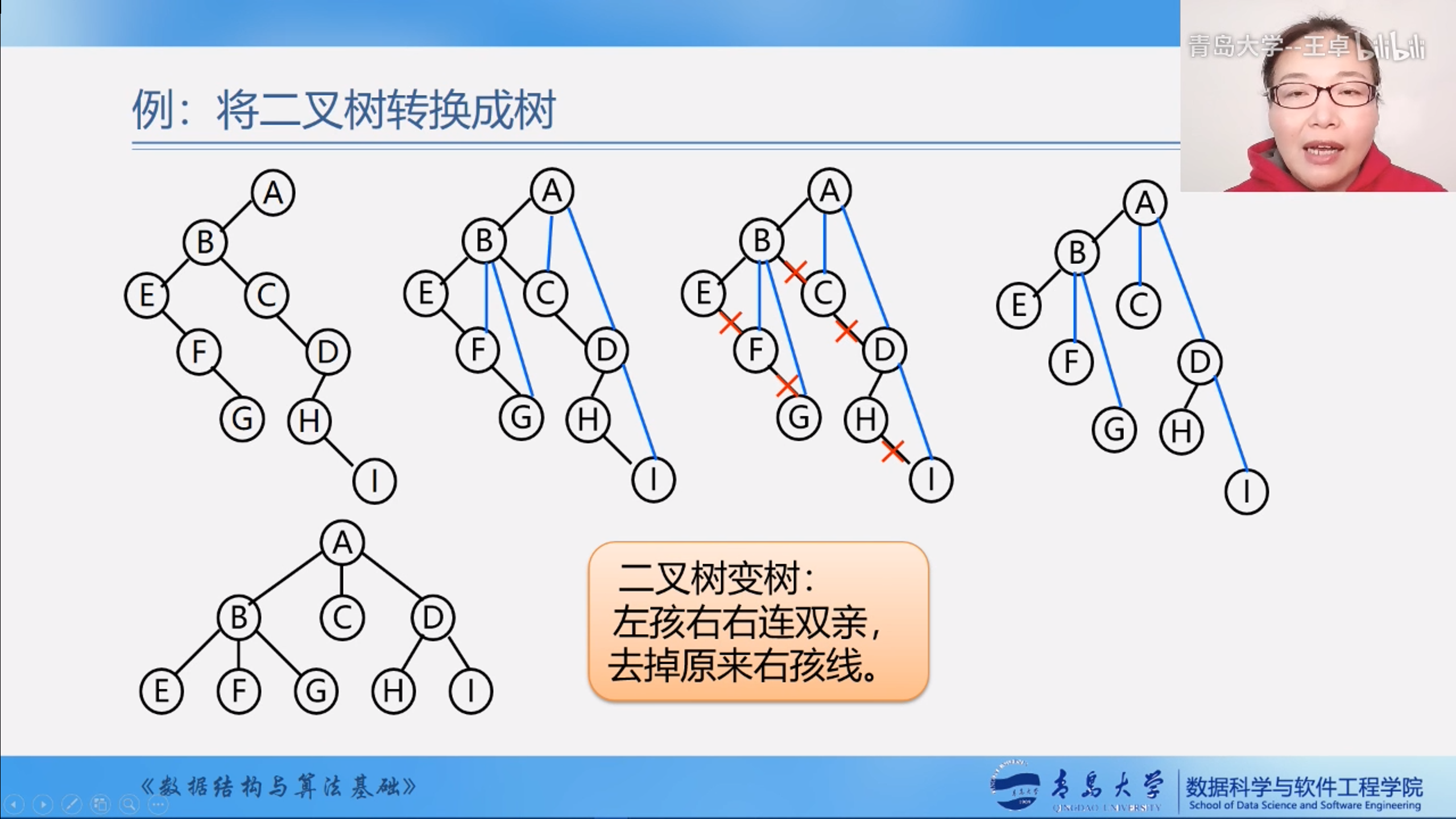
例子

森林和二叉树的转换

树变二叉根相连

1. 将各树转换为二叉树
2. 将每颗树的根结点用线相连
3. 将第一颗树的根结点作为二叉树的根,再以根结点为轴心,顺时针旋转.

树变二叉树

兄弟相连,留长子.

森林变二叉树

树边二叉根相连

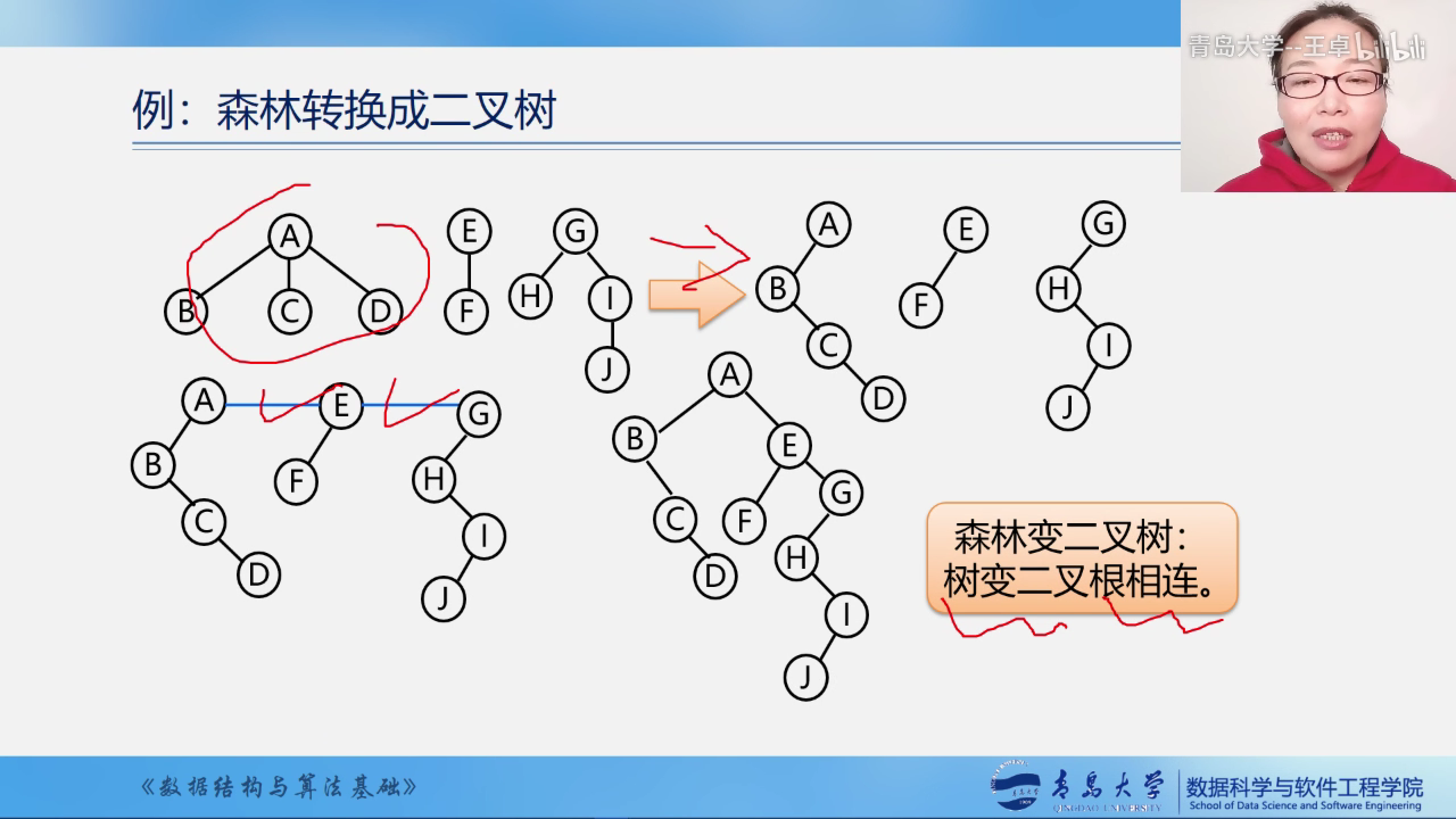
二叉树转化为森林

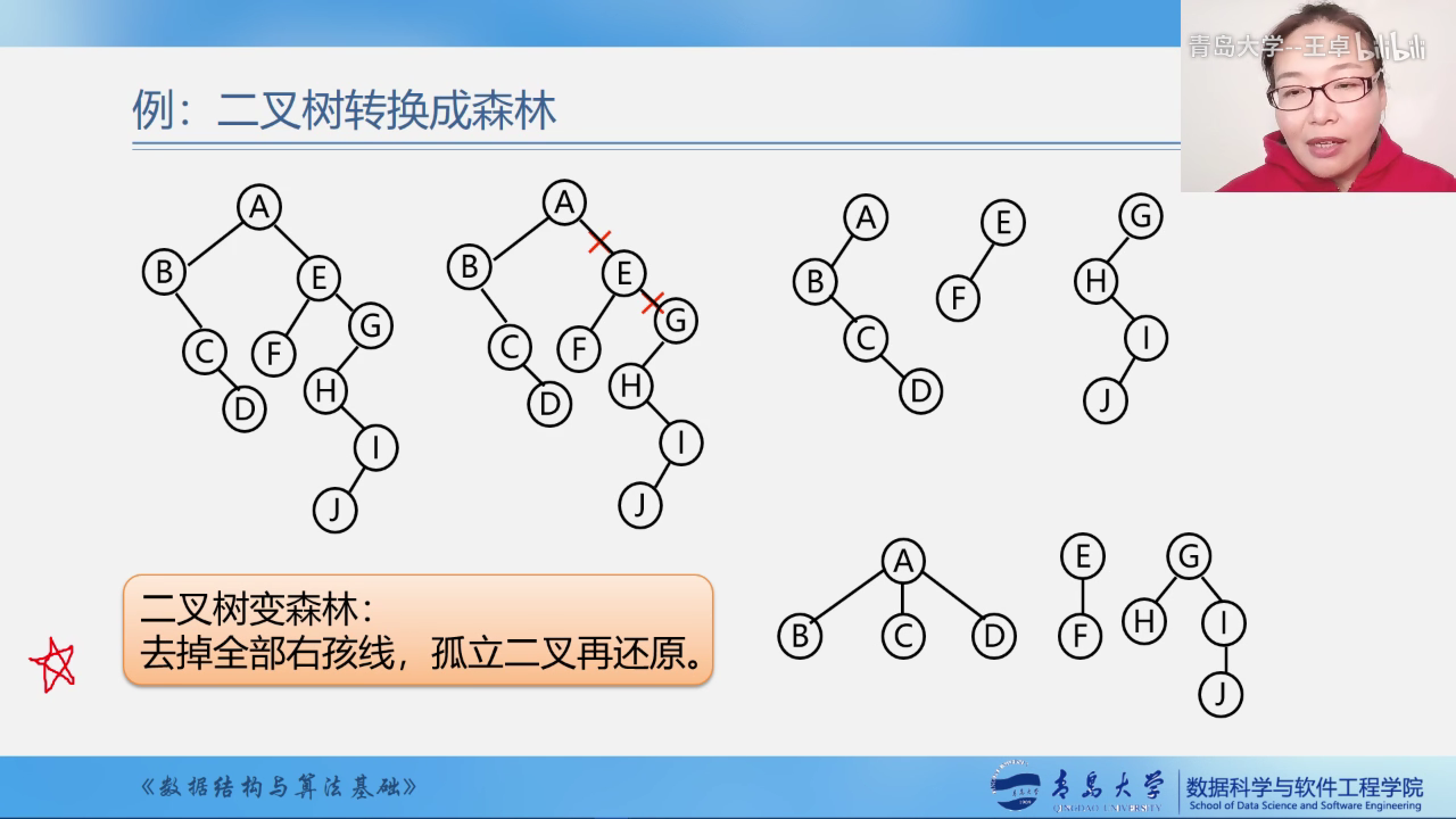
1. 抹线
2. 还原

去掉全部右孩线,孤立二叉再还原.

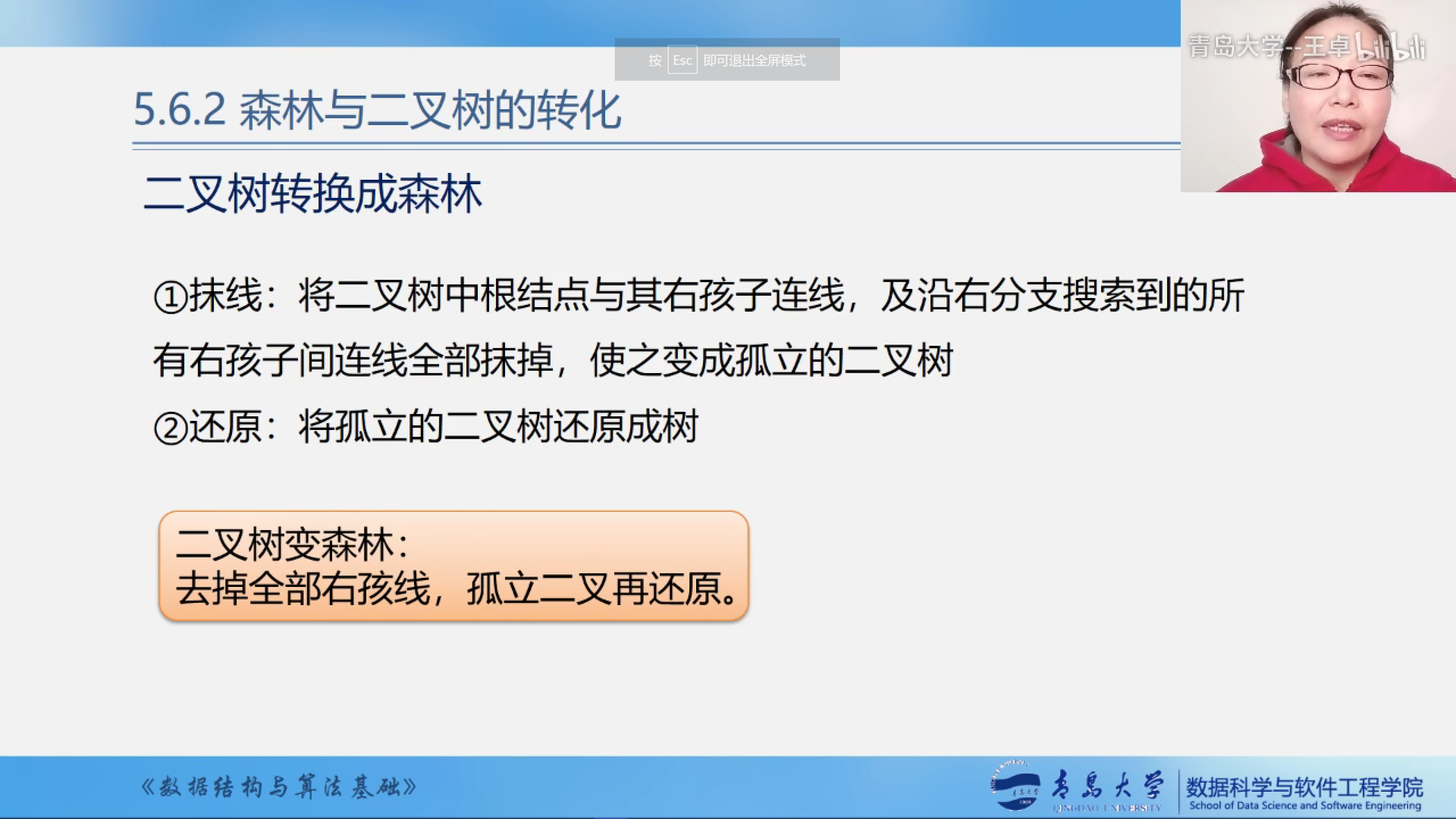
二叉树转化为树

左孩右右连双亲,去掉原来右孩线.

树和森林的遍历

树的遍历

1. 先根遍历

2. 后根遍历

3. 层次遍历

   树没有中序遍历方式.

   

森林的遍历

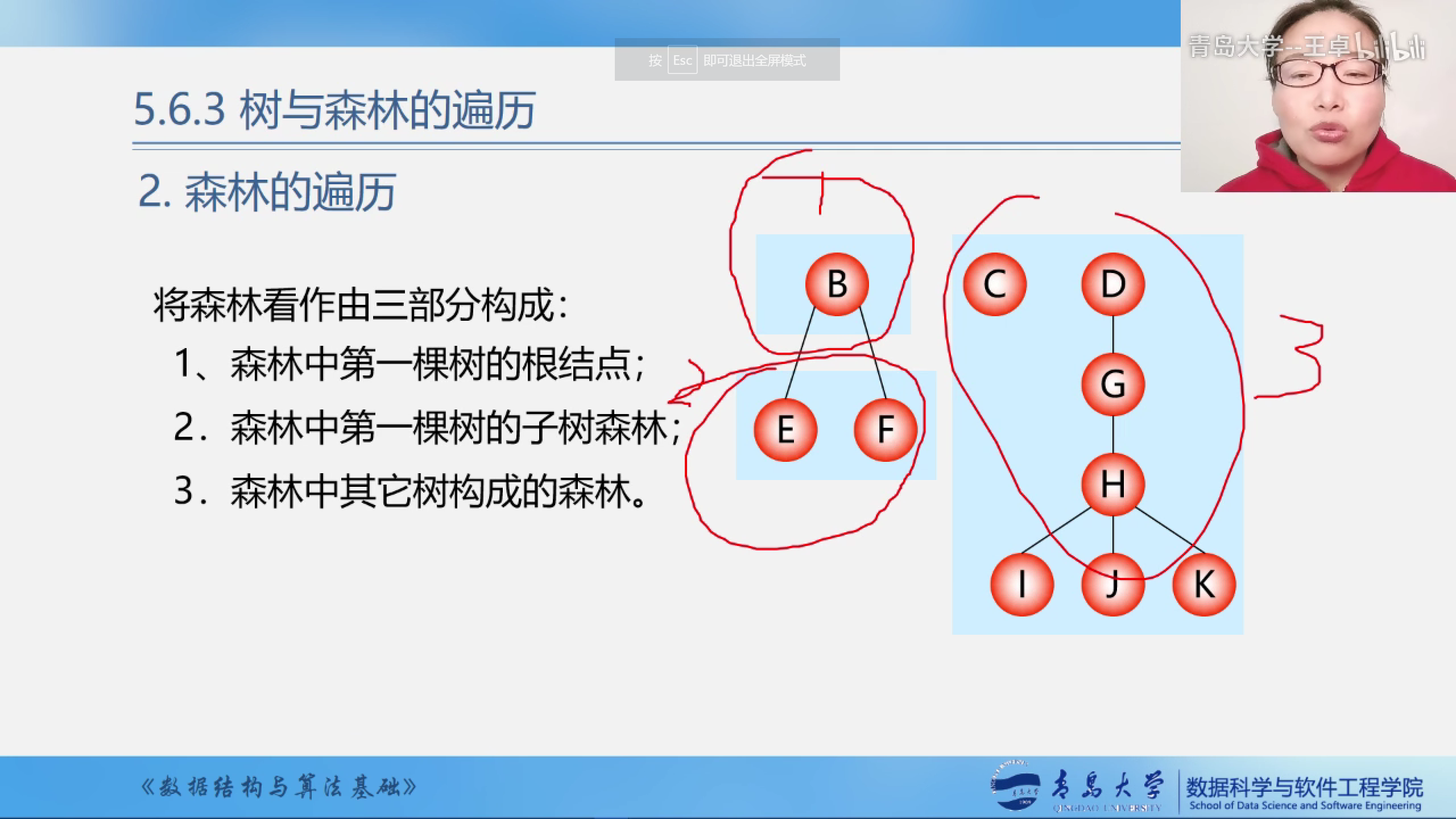
将森林看成3部分.分别遍历这3个部分

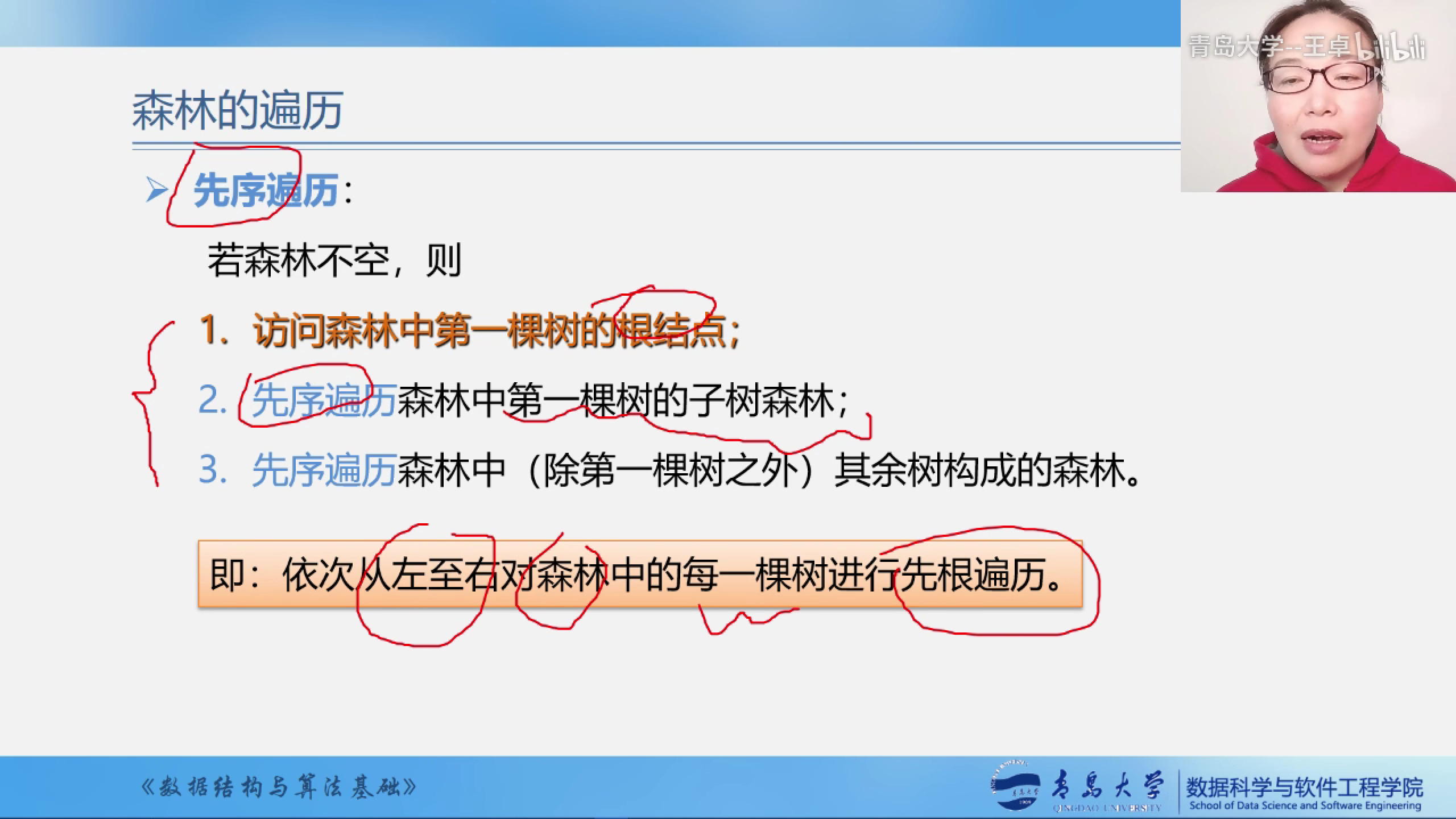
先序遍历

依次从左到右对森林中的每一棵树进行先序遍历

先访问根结点然后访问左子树,然后再访问右子树

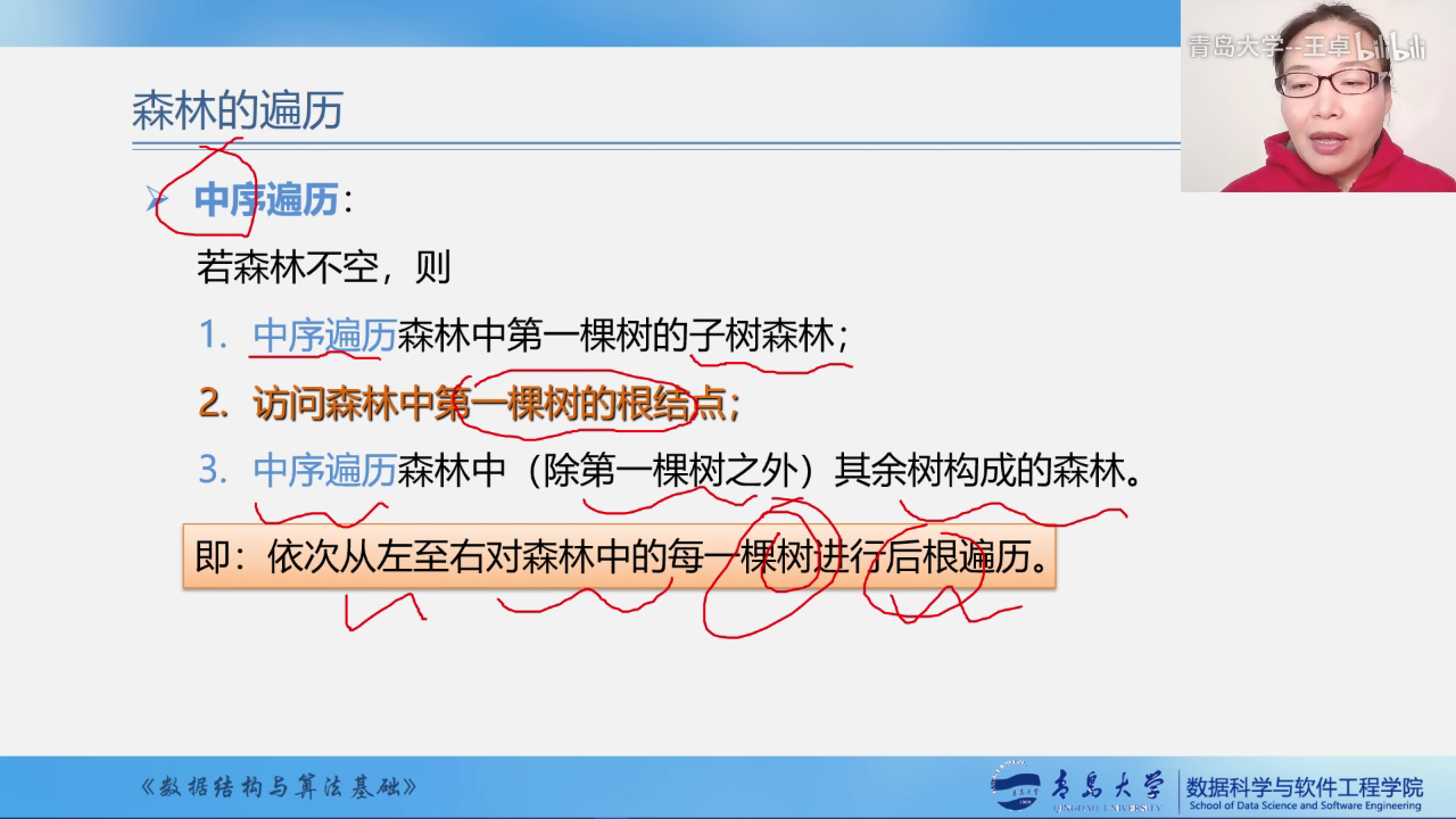
中序遍历

依次从左到右对每一棵树进行后根遍历

例题:森林的遍历