数据结构--平衡二叉树

平衡二叉树

回顾:二叉排序树的查找

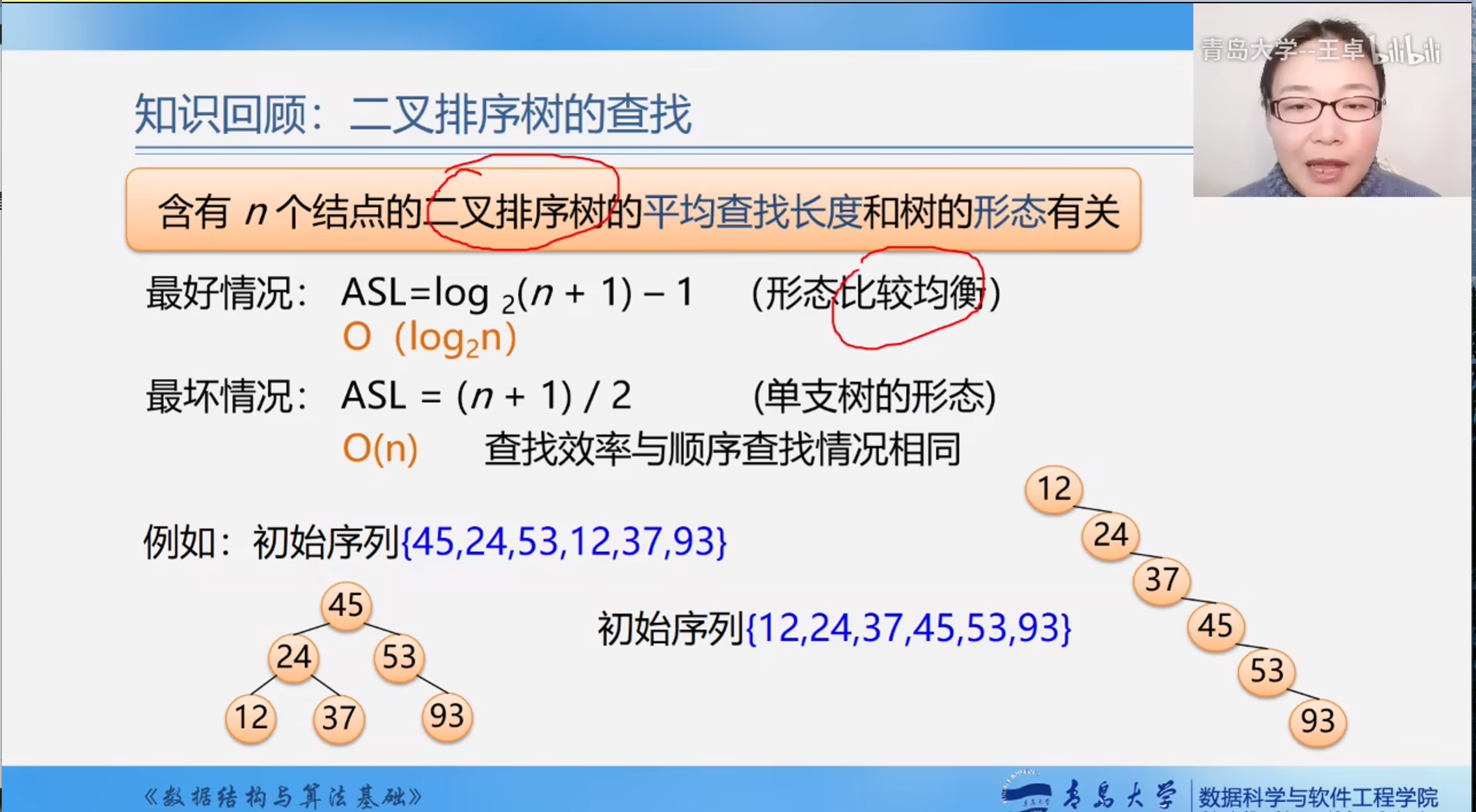
二叉排序树的不平衡会影响查找效率,所有我们要尽量让二叉树的形态均衡.

AVL树(平衡二叉树)

1. 必须是二叉排序树

2. 左子树和右子树的高度之差的绝对值小于等于1

3. 左子树和右子树也是平衡二叉排序树

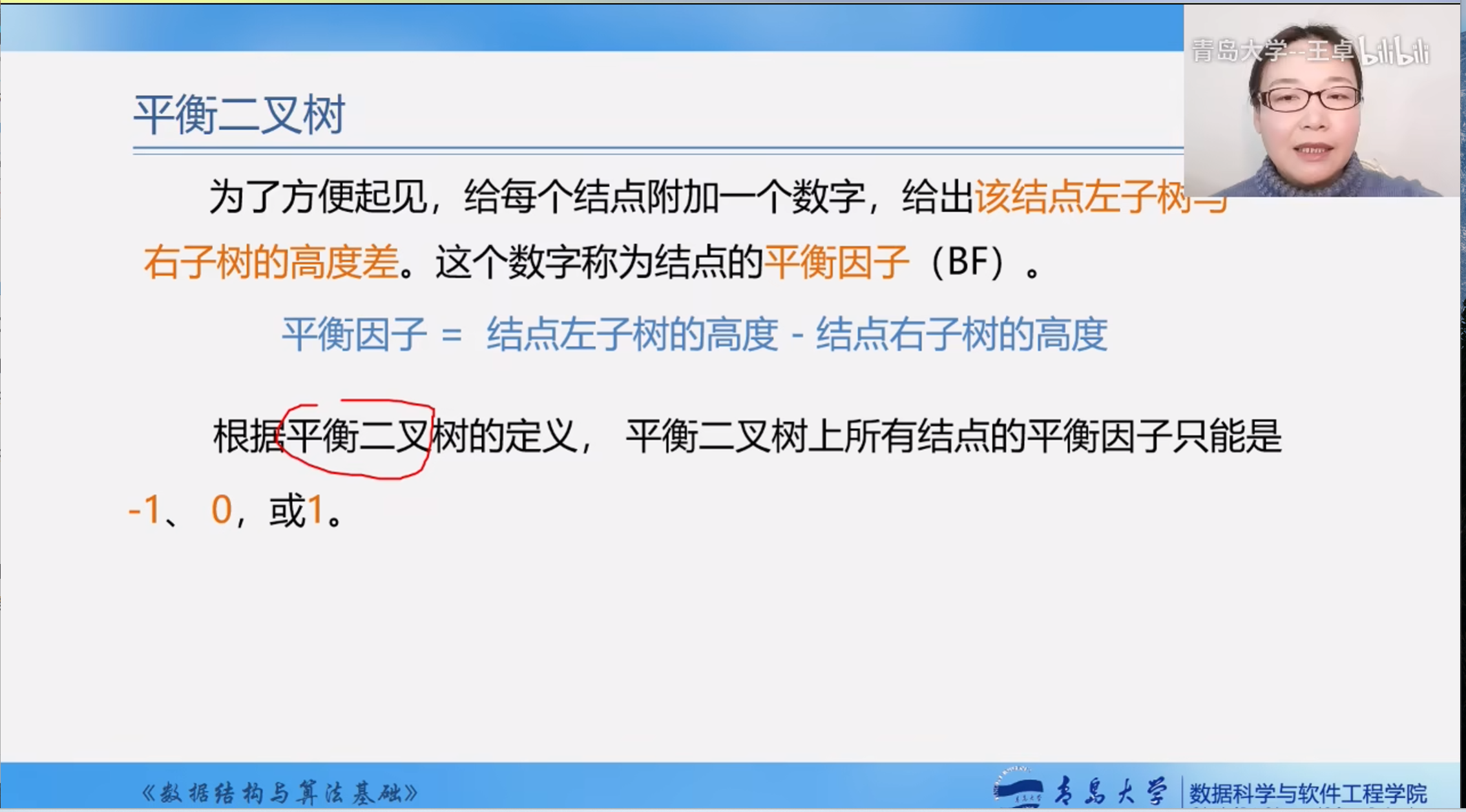
   平衡因子

   该结点左子树与右子树的高度差.

   平衡因子=结点左子树的高度-结点右子树的高度

判断平衡二叉树

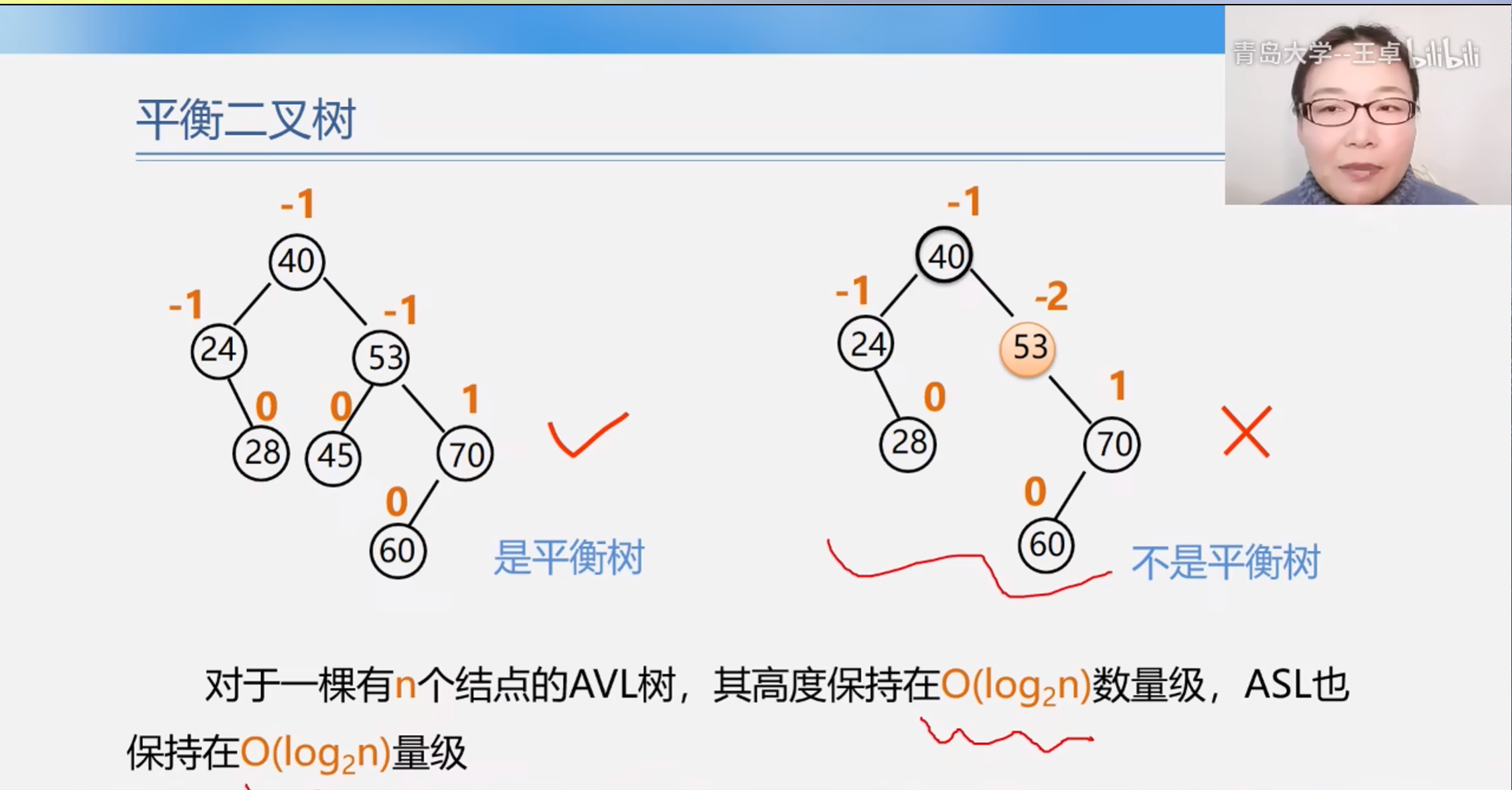
对于一个右n个结点的AVL树,其高度保持再O(logn)数量级,ASLA也保持在O(logn)量级.

平衡调整办法1

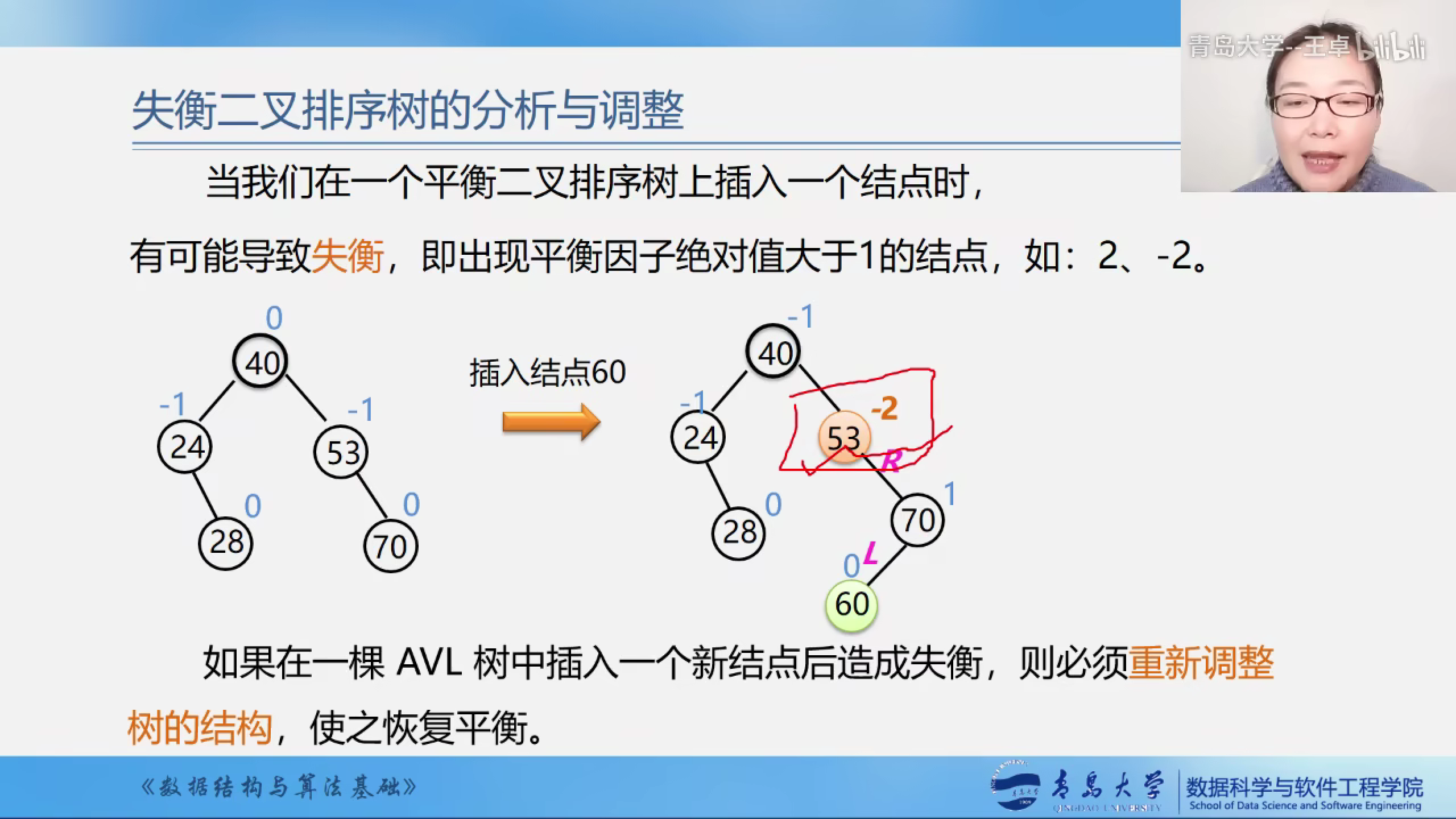
有可能导致失衡,即出现平衡因子大于1的结点

如果在一颗AVLA树中插入一个新结点后造成失衡,则必须重新调整树的结构,让其恢复平衡

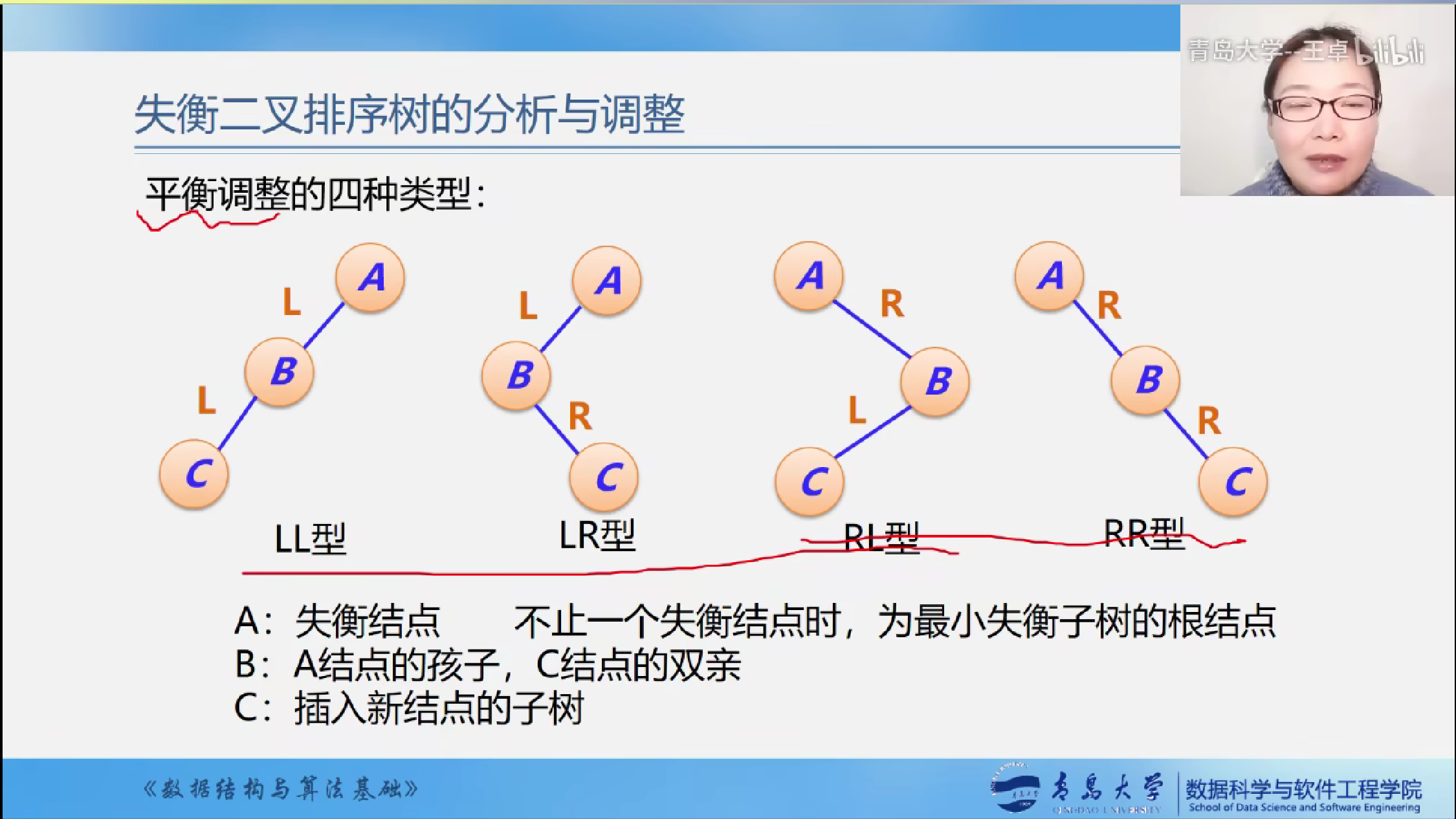
平衡调整的四种类型

A:失衡结点 不止一个失衡结点时,为最小失衡子树的结点

B:A结点的孩子,C结点的双亲.

C:插入新节点的子树.

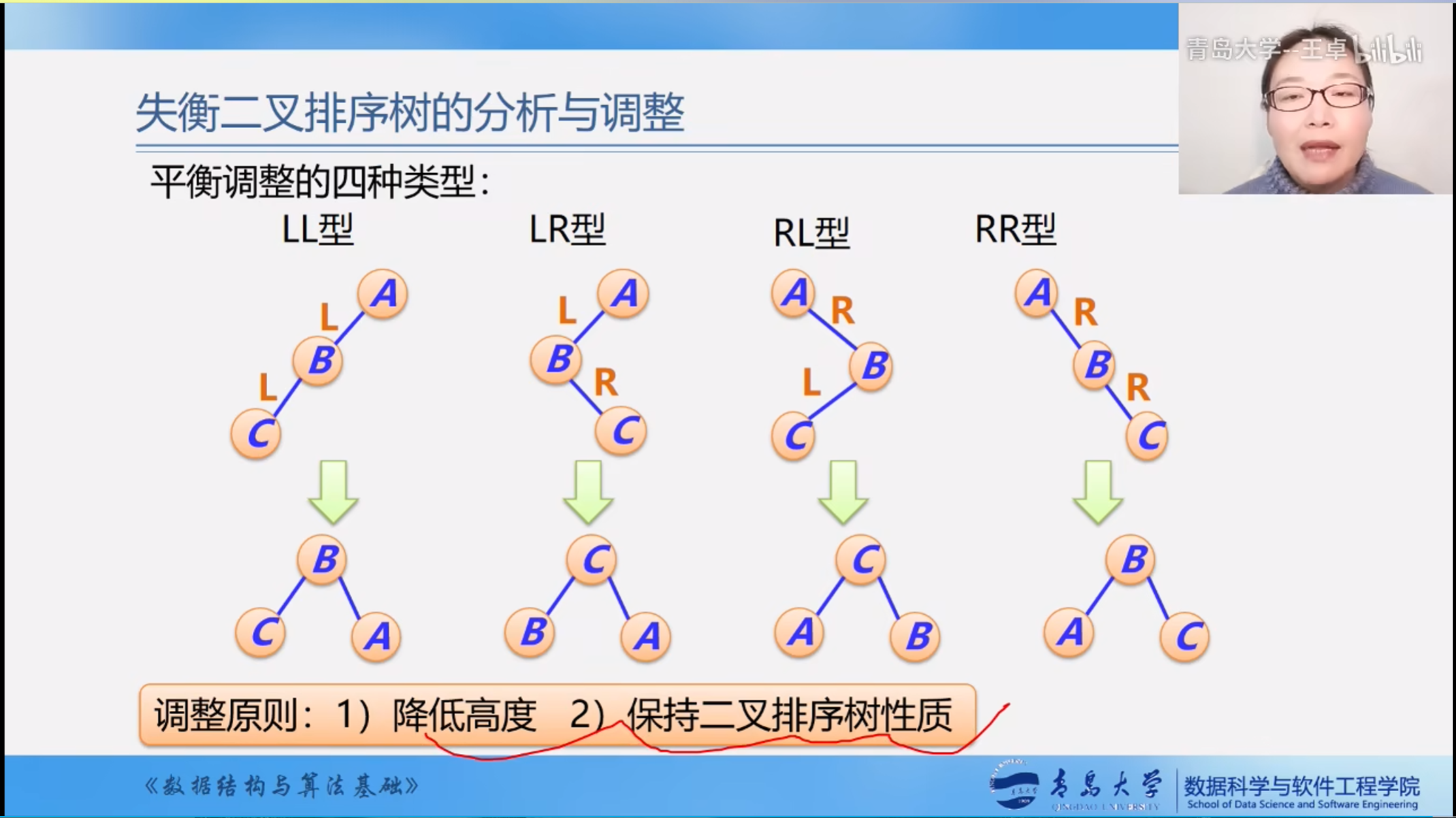
调整原则:

1. 降低高度
2. 保持二叉排序树性质

LL型

1. B结点带左子树α一起上升
2. A结点成为B的右孩子
3. 原来B结点的右子树β作为A的左子树

LL型例题

RR型调整

1. B结点带右子树β一起上升
2. A结点成为B的左孩子
3. 原来B结点的左子树α作为A的右子树

RR型例子

LR型调整

C是最小的所以要上升

1. C结点穿过A、B结点上升
2. B结点成为C的左孩子，
3. A结点成为C的右孩子
4. 原来C结点的左子树β作为B的右子树；
5. 原来C结点的右子树y作为A的左子树

LR型例题

RL型调整

C最小所以C做为根结点

1. C结点穿过A、B结点上升

2. A结点作为C结点的左孩子

3. B结点作为C结点的右孩子

4. 原来C结点的左子树β作为A的右子树；
5. 原来C结点的右子树y作为B的左子树

---

RL型例子

平衡二叉树的调整例题

插入7 进行LR型调整

插入9 进行LL型调整

插入26 进行RR调整

插入18 进行RL调整

插入14

插入15 进行LR调整,调整最小失衡的子树

AVL树构造完毕