自控元件 第0章 磁路及其计算

绪论

本门课程教授控制系统中部分典型执行元件的工作原理、技术指标、和使用方法等，并且专注于那些以电磁为能量中介的执行元件。

至少PPT是这么说的，现在一学期学完学完后我感觉主要学到了不同电机的工作原理，有多大用还不知道。

第0章 磁路及其计算

本章的内容是做了很多近似的，不能用电磁场、甚至不能用大物的标准来抠细节（我也不会哈哈）。。。

0.1 磁路的基本物理量和基本定律

磁场的基本物理量

基本沿用大物的内容，做简要回顾。

• 磁感应强度/磁密\(\boldsymbol B\)：一种用矢量场描述磁现象的方法，其定义不是本门课的重点。

• 磁场强度\(\boldsymbol H=\frac{\boldsymbol B}{\mu}\)（在均匀、各向同性、线性介质内）：另一种用矢量场描述磁现象的方法，其定义不是本门课的重点。

  • 磁导率：表示物质导磁能力大小的物理量，用\(\mu\)表示。

• 磁通量/磁通\({\rm d}\phi=\boldsymbol B\cdot \boldsymbol {{\rm d} A}\)：磁场对某一曲面的面积分。

  • 本门课只讨论均匀的磁场，不均匀的也近似为均匀的，所以也有\(\phi=BA\)。

• 磁路：磁场所形成的闭合回路称为磁路。不过本门课关注的是经过铁磁材料以及铁磁材料间的气隙的磁路。

  • 主磁通：通过主要磁路的磁通，用\(\phi_0\)表示。
  • 漏磁通：另外少量的磁通不在主磁通中的磁通，用\(\phi_s\)表示。

• 磁链\(\varPhi=N\phi\)：通过多匝线圈的磁通。

  本门课讨论的磁场几乎都是由线圈产生的。

• 自感\(L=\frac{\psi}{I}\)：描述线圈中的电流与该电流在其自身所围面积上所产生的磁链的关系。

• 互感\(M=\frac{N_1\phi_{21}}{I_2}=\frac{N_2\phi_{12}}{I_1}\)：描述一个线圈的电流与该电流在另一线圈所围面积上所产生的磁链的关系。\(\phi_{12}\)表示线圈1在线圈2所围面积上所产生的磁通量，\(N_2\)是线圈2的匝数。

  • 互感的同名端：当两个线圈的电流共同从各自的*流入或流出时，其磁场相互加强，互感大于0；反之则相互削弱，互感小于0。用*表示同名端。

在磁路上新定义的量

• 磁压降\(\mathrm d U_m=\boldsymbol H\cdot \mathrm d l\)

  • 注意本门课只讨论均匀的磁场，不均匀的也近似为均匀的，所以也有\(U_m=HL\)。

• 磁（动）势\(F_m=IN\)

  • 物理意义同电磁场里所讲的磁标矢，维基百科上定义为磁动势；本课只是为了计算方便而引入了该量，简称为磁势。

    在一个单连通、没有自由电流的区域里，可以定义磁标势\(\psi\)为

    \[\boldsymbol H=-\nabla\psi \]

    更详细的信息可以参考维基百科条目“磁标矢”和“磁动势”。

  • 电流所产生的磁场的方向为高磁势。

• 磁阻\(R_m=\frac{U_m}{\phi}=\frac{BL}{\mu BA}=\frac{L}{\mu A}\)

  • 针对一个截面积、磁导率都均匀的介质做的定义。

磁场的基本定律

仍然是简要回顾大物内容。

• 安培力\(\mathrm d\boldsymbol F=I\mathrm d\boldsymbol l\times \boldsymbol B\)：通电导体在磁场中受力地规律，其中\(\boldsymbol l\)的指向电流流动的方向
  • 注意本门课只讨论均匀的磁场，不均匀的也近似为均匀的，所以也有\(\boldsymbol F=I\boldsymbol L\times \boldsymbol B\)。
• 电磁感应\(e=-N\frac{\mathrm d\phi}{\mathrm d t}\)
  • 方向可以由楞次定律判断：感应电流的磁场总要阻碍引起感应电流的磁通量的变化。

磁路的基本定律

由磁场的高斯定理可以得到磁路基尔霍夫第一定律，由安培环路定理可以得到磁路基尔霍夫第二定律。

类比电路看的最清楚：

电路	磁路
电动势\(E\)	磁（动）势\(F_m=NI\)
电压降\(U=IR\)	磁压降\(U_m=\phi R_m\)
电流\(I\)	磁通\(\phi\)
电阻\(R=\frac{l}{\gamma A}\)	磁阻\(R_m=\frac{l}{\mu A}\)
电导率\(\gamma\)	磁导率\(\mu\)
基尔霍夫第一定律\(\sum I=0\)	磁路基尔霍夫第一定律\(\sum \phi=0\)
基尔霍夫第二定律\(\sum U=\sum E\)	磁路基尔霍夫第二定律\(\sum U_m=\sum F_m\)

0.2 磁化、磁滞和涡流

磁化

• 物质的导磁性能：不同物质放在磁场\(\boldsymbol H\)中，其内部会产生不同的\(\boldsymbol B\)。其中铁磁物质因为磁化作用其产生的\(\boldsymbol B\)会较大，也即\(\mu\)较大。

  • 磁化：是指在受磁场的作用下，由于材料中磁矩排列时取向趋于一致而呈现出一定的磁性的现象。

• 磁饱和：外磁场过大之后铁磁物质的\(\mu\)又会减小，产生的\(\boldsymbol B\)随\(\boldsymbol H\)的增长减缓。

  

  ①是真空中的\(\boldsymbol B=\mu_0\boldsymbol H\)；②是铁磁物质中的\(\boldsymbol B=\mu\boldsymbol H\)；③是铁磁物质中的\(\mu-H\)关系。

• 温度特性：温度上升到一定时，铁磁材料会转化为弱磁物质，该温度称为居里点。

铁心损耗

包含磁滞损耗和涡流损耗。

磁滞损耗

• 磁滞：将铁磁材料从原始状态逐步磁化，再退磁，则磁感应强度\(B\)的变化总是会落后于外磁场\(H\)的变化的现象。

  

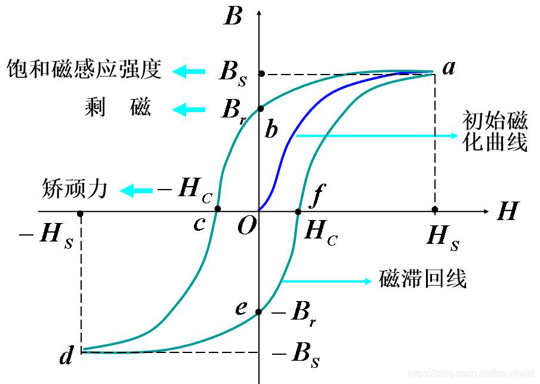
• 磁滞损耗：磁滞现象会发热而引起损耗。

• 铁磁材料的分类

  • 软磁材料：\(B_r\)、\(H_c\)较小，磁滞回线较窄，磁滞损耗小，比如铸铁、硅钢、坡莫合金等，适合做铁心。
  • 硬磁材料：\(B_r\)、\(H_c\)较大，磁滞回线较宽，磁滞损耗大，比如钨钢、钴钢、镍钴合金、稀土合金等，适合做永久磁铁。

涡流损耗

• 涡流：铁磁材料在交变磁化过程中会产生感应电势和感应电流，该电流在铁心中会环绕磁力线做旋涡状分布的现象。
• 涡流损耗：涡流现象同样会发热而产生损耗。
  • 缓解方法
    • 电工钢片叠压做铁心
    • 钢片间刷绝缘漆、钢片材料中加硅，以增加电阻率

0.3 直流磁路的计算

• 已知磁通求磁势：

  气隙上的磁压降

  \[\phi\stackrel{R_m}{\longrightarrow}U_m \]

  铁心上的磁压降

  \[\phi\stackrel{A}{\longrightarrow} B\stackrel{用\mu计算或者查表}{\longrightarrow} H\stackrel{L}{\longrightarrow} U_m \]

  最后使用磁路基尔霍夫第二定律\(\sum U_m=\sum F_m\)即可。

• 已知磁势求磁通

  困难在于铁心磁阻没有确定的公式反推，就像是电路题中遇到了一个随电流非线性变化的电阻。

  • 猜试法：估算出磁通，然后按“已知磁通求磁势”的流程估算磁势，然后与给定磁势比较，误差在10%内（教材）认为可以接受。
  • 图解法
    • 作出铁心的\(\phi-U_m\)曲线（可由磁化曲线拉伸得到）
    • 求气隙的磁阻\(R_m\)，作出\(\phi=\frac{F_m-U_m}{R_m}\)曲线
    • 确定两曲线的焦点，即为对应的\(\phi\)

0.4 交流磁路及其计算

特点

• 因为磁饱和，磁通、电流会畸变

  正弦磁通会产生尖顶电流，正弦电流会产生平顶磁通。

• 因为磁场变化，存在铁心损耗

• 因为磁场变化，存在感应电动势

等值电路

要注意考虑漏磁通的影响，具体来说可以等效为一个电感。本节没有怎么展开。