P10149 [Ynoi1999] XM66F 题解

分析

考虑莫队。

对于 \(a_i=k(l \le i \le r)\) 的下标集合 \(S_k\)，当其加入一个新的下标 \(x\) 时，这个新下标对答案的贡献分两种情况。

第一种，\(x\) 最小。相邻从下标的间隔中产生的贡献是 \(\sum (|S_k|-i+1)\times(ans_{S_{k,i+1}}-ans_{S_{k,i}})\)。画个图可以理解一下：

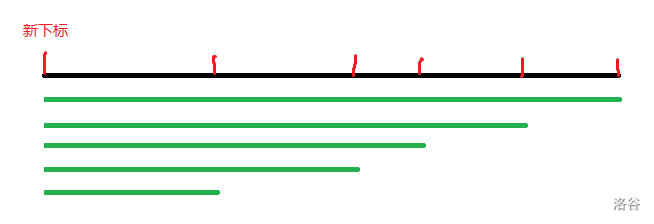
第二中，\(x\) 最大。相邻从下标的间隔中产生的贡献是 \(\sum i\times(ans_{S_{k,i+1}}-ans_{S_{k,i}})\)。画个图可以理解一下：

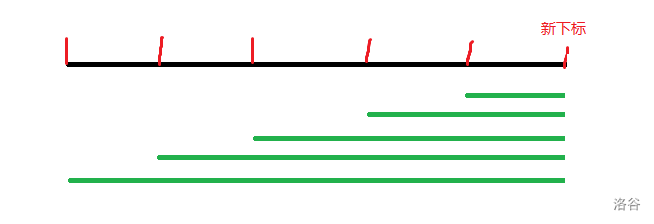
其中绿色部分是产生的贡献，\(ans_i\) 表示前 \(i\) 个数中小于 \(a_i\) 的数量。

然后就是把上面的情况在莫队里 \(O(1)\) 更新。很简单，考虑前缀和优化。定义 \(s_i = \sum\limits_{j=1\land S_{a_i,j} \le i}^{|S_{a_i}|} ans_{S_{a_i,j}}\)。

第一种情况有 \(\sum (|S_k|-i+1)\times(ans_{S_{k,i+1}}-ans_{S_{k,i}})=s_{S_{k,|S_k|}}-s_{S_{k,1}}-(|S_k|-1) \times ans_{S_{k,1}}\)。其实就是找到当前区间的区间和在减掉多出算的。画个图可以理解一下：

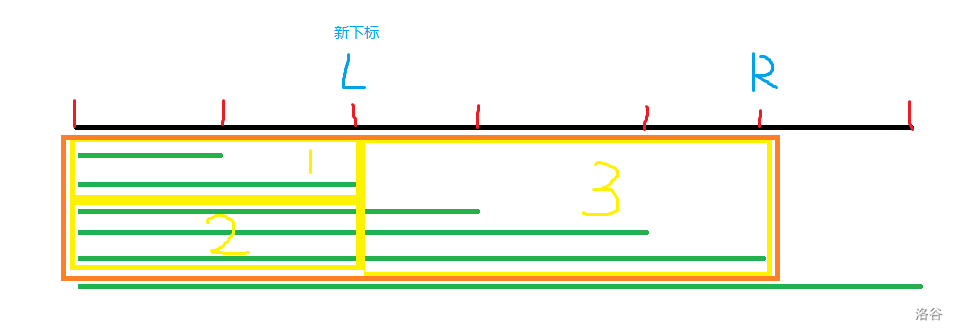
橙色部分是前缀和，需要保留 \(3\) 部分，第一次减掉 \(1\) 部分，第二次减掉 \(2\) 部分。

第二种情况同理，可以自己推一下。

复杂度 \(O(n \log n +n\sqrt{n})\)。

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define re register
#define il inline
#define pii pair<int,int>
#define x first
#define y second
#define gc getchar()
#define rd read()
#define debug() puts("------------")

namespace yzqwq{
	il int read(){
		int x=0,f=1;char ch=gc;
		while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=gc;}
		while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+(ch^48),ch=gc;
		return x*f;
	}
	il int qmi(int a,int b,int p){
		int ans=1;
		while(b){
			if(b&1) ans=ans*a%p;
			a=a*a%p,b>>=1;
		}
		return ans;
	}
	il auto max(auto a,auto b){return (a>b?a:b);}
	il auto min(auto a,auto b){return (a<b?a:b);}
	il int gcd(int a,int b){
		if(!b) return a;
		return gcd(b,a%b);
	}
	il int lcm(int a,int b){
		return a/gcd(a,b)*b;
	}
	il void exgcd(int a,int b,int &x,int &y){
		if(!b) return x=1,y=0,void(0);
		exgcd(b,a%b,x,y);
		int t=x;
		x=y,y=t-a/b*x;
		return ;
	}
	mt19937 rnd(time(0));
}
using namespace yzqwq;

const int N=5e5+10;
int n,m,a[N],w[N];
struct Query{
	int l,r,id;
}Q[N];
int len,sum,ans[N];
vector<int> x[N];
int s[N];
int cnt[N],Cnt[N];
int tr[N],pre[N],nxt[N],lst[N];
int L[N],R[N];

il void add(int x){
	while(x<=n) ++tr[x],x+=x&(-x);
}
il int query(int x){
	int ans=0;
	while(x) ans+=tr[x],x-=x&(-x);
	return ans;
}
il bool cmp(Query a,Query b){
	if(a.l/len!=b.l/len) return a.l<b.l;
	if((a.l/len)&1) return a.r<b.r;
	return a.r>b.r;
}
il void Add(int id,int f){
	int x=a[id];
	++Cnt[x];
	if(Cnt[x]==1) return L[x]=R[x]=id,void(0);
	if(f==1){
		L[x]=id;
		sum+=s[R[x]]-s[L[x]]-(Cnt[x]-1)*cnt[id];
	}
	else{
		R[x]=id;
		sum+=s[pre[L[x]]]+(Cnt[x]-1)*cnt[id]-s[pre[R[x]]];
	}
	return ;
}
il void Del(int id,int f){
	int x=a[id];
	--Cnt[x];
	if(Cnt[x]==0) return L[x]=R[x]=0,void(0);
	if(f==1){
		sum-=s[R[x]]-s[L[x]]-Cnt[x]*cnt[id];
		L[x]=nxt[id];
	}
	else{
		sum-=s[pre[L[x]]]+Cnt[x]*cnt[id]-s[pre[R[x]]];
		R[x]=pre[id];
	}
	return ;
}

il void solve(){
	n=rd,m=rd,len=sqrt(n);
	for(re int i=1;i<=n;++i) x[i].push_back(0);
	for(re int i=1;i<=n;++i) a[i]=rd,x[a[i]].push_back(i),w[i]=x[a[i]].size();
	for(re int i=1;i<=m;++i) Q[i]={rd,rd,i};
	sort(Q+1,Q+m+1,cmp);
	
	for(re int i=1;i<=n;++i) cnt[i]=query(a[i]-1),add(a[i]);
	for(re int i=1;i<=n;++i){
		s[i]=cnt[i]+s[lst[a[i]]];
		nxt[lst[a[i]]]=i,pre[i]=lst[a[i]],lst[a[i]]=i;
	}
	
	int l=1,r=0;
	for(re int i=1;i<=m;++i){
		while(l>Q[i].l) Add(--l,1);
		while(r<Q[i].r) Add(++r,2);
		while(l<Q[i].l) Del(l++,1);
		while(r>Q[i].r) Del(r--,2);
		ans[Q[i].id]=sum;
	}
	for(re int i=1;i<=m;++i) printf("%lld\n",ans[i]);
	return ;
}

signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	int t=1;while(t--)
	solve();
	return 0;
}