蓝桥杯刷题记录

1.近似 GCD

题目描述

小蓝有一个长度为 n 的数组 A = (a1, a2, · · · , an)，数组的子数组被定义为从原数组中选出连续的一个或多个元素组成的数组。数组的最大公约数指的是数组中所有元素的最大公约数。如果最多更改数组中的一个元素之后，数组的最大公约数为 g，那么称 g 为这个数组的近似 GCD。一个数组的近似 GCD 可能有多种取值。

具体的，判断 g 是否为一个子数组的近似 GCD 如下：

1. 如果这个子数组的最大公约数就是 g，那么说明 g 是其近似 GCD。

2. 在修改这个子数组中的一个元素之后（可以改成想要的任何值），子数组的最大公约数为 g，那么说明 g 是这个子数组的近似 GCD。

小蓝想知道，数组 A 有多少个长度大于等于 2 的子数组满足近似 GCD 的值为 g。

输入格式

输入的第一行包含两个整数 n, g，用一个空格分隔，分别表示数组 A 的长度和 g 的值。

第二行包含 n 个整数 a1, a2, · · · , an，相邻两个整数之间用一个空格分隔。

输出格式

输出一行包含一个整数表示数组 A 有多少个长度大于等于 2 的子数组的近似 GCD 的值为 g 。

样例输入

复制

5 3
1 3 6 4 10

样例输出

复制

5

提示

满足条件的子数组有 5 个：

[1, 3]：将 1 修改为 3 后，这个子数组的最大公约数为 3 ，满足条件。

[1, 3, 6]：将 1 修改为 3 后，这个子数组的最大公约数为 3 ，满足条件。

[3, 6]：这个子数组的最大公约数就是 3 ，满足条件。

[3, 6, 4]：将 4 修改为 3 后，这个子数组的最大公约数为 3 ，满足条件。

[6, 4]：将 4 修改为 3 后，这个子数组的最大公约数为 3，满足条件。

对于 20% 的评测用例，2 ≤ n ≤ 102 ；

对于 40% 的评测用例，2 ≤ n ≤ 103；

对于所有评测用例，2 ≤ n ≤ 105 , 1 ≤ g, ai ≤ 109。

思路一

1. 创建数组arr
2. 遍历数组首先选出能够整除g的所有元素，打上标记
3. 获取打上标记的数组元素索引组成的数组arr_true
4. 使用数组arr的长度进行遍历，同时遍历arr_true数组，找出可能与arr_true数组中元素相连的子数组数量

#include<iostream>
using namespace std;

// 定义结构体，方便判断能否被gcd整除
struct num{
    int value;
    bool isreduce;
};

int countTrue(int arr[], int length){
    int count = 0;
    for (int i = 0; i < length; ++i) {
        if (arr[i] == 1){
            count++;
        }
    }
    return count;
}

int main() {
    freopen("a.in", "r", stdin);
    freopen("a.out", "w", stdout);
    int length;
    int g;
    cin >> length >> g;
    int arr[length];
    num arr1[length];
    for (int i = 0; i < length; ++i) {// 接受输入
        cin >> arr[i];
    }

    for (int i = 0; i < length; ++i) {
        int temp = arr[i] % g;
        if (temp != 0 ){ // 如果不能被整除
            arr1[i].value = arr[i];
            arr1[i].isreduce = false;
        }
        else{
            arr1[i].value = arr[i];
            arr1[i].isreduce = true;
        }
    }

    // 分割成子数组，且子数组的元素数量大于等于2
    // 或者获取num.isreduce组成的数组

    for (int i = 0; i < length; ++i) {
        arr[i] = arr1[i].isreduce;

    }

    //获取num中1的索引
    int count = countTrue(arr,length);
    int arr_true[count];
    int temp = 0;
    for (int i = 0; i < length; ++i) {
        if(arr[i] == 1){
            arr_true[temp] = i;
            temp++;
        }
    }

    // 数组长度为length
    int result = 0;
    for (int i = 0; i < length; ++i) {
        int t = i;
        for (int j = 0; j < count; ++j) {
            if(arr_true[j] == t - 1){
                continue;
            }
            if(arr_true[j] == t){
                result++;
                t++;
                continue;
            }
            if(arr_true[j] == t + 1){
                result++;
                t++;
            }
        }
    }
    cout << result;

    return 0;
}

结果

时间超限 22分

思路二

1. 使用辗转相除法定义一个求最大公约数的函数gcd。
2. 使用两个指针，用来指出前后的数组长度，该数组为包含一个不为g的倍数的子数组。
3. 当第一个数满足条件时，但不满足数组长度为2，result不会增加。
4. 当一直不满足条件时，需要一个标记last，区别于j，一直指向不满足条件的数，且为上一个满足条件的最长子数组的下一个不满足条件的数。
5. 直到寻找到下一个满足条件的值时，将result + = i - j。
6. 当下一个值不满足条件时，将i赋值给last，并将j = last + 1。

结果

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, g;
int a[N];

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}


int main()
{
    freopen("a.in", "r", stdin);
    freopen("a.out", "w", stdout);
    scanf("%d%d", &n, &g);

    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    int last = 0;
    long long res = 0;
    for (int i = 1, j = 1; i <= n; i ++ )
    {
        int t = gcd(g, a[i]);
        if (t != g) j = last + 1, last = i;
        if (i - j + 1 >= 2) res += i - j;
    }

    printf("%lld", res);

    return 0;
}

2.2728: 交通信号

题目描述

LQ 市的交通系统可以看成由 n 个结点和 m 条有向边组成的有向图。在每条边上有一个信号灯，会不断按绿黄红黄绿黄红黄... 的顺序循环 (初始时刚好变到绿灯)。当信号灯为绿灯时允许正向通行，红灯时允许反向通行，黄灯时不允许通行。每条边上的信号灯的三种颜色的持续时长都互相独立，其中黄灯的持续时长等同于走完路径的耗时。当走到一条边上时，需要观察边上的信号灯，如果允许通行则可以通过此边，在通行过程中不再受信号灯的影响；否则需要等待，直到允许通行。请问从结点 s 到结点 t 所需的最短时间是多少，如果 s 无法到达 t 则输出−1。

输入格式

输入的第一行包含四个整数 n, m, s, t，相邻两个整数之间用一个空格分隔。

接下来 m 行，每行包含五个整数 ui, vi, gi,ri, di ，相邻两个整数之间用一个空格分隔，分别表示一条边的起点，终点，绿灯、红灯的持续时长和距离（黄灯的持续时长）。

输出格式

输出一行包含一个整数表示从结点 s 到达 t 所需的最短时间。

样例输入

4 4 1 4
1 2 1 2 6
4 2 1 1 5
1 3 1 1 1
3 4 1 99 1

样例输出

11

提示

对于 40% 的评测用例，n ≤ 500 ，1 ≤ gi,ri, di ≤ 100 ；

对于 70% 的评测用例，n ≤ 5000 ；

对于所有评测用例，1 ≤ n ≤ 100000 ，1 ≤ m ≤ 200000 ，1 ≤ s, t ≤ n ，1 ≤ ui, vi ≤ n ，1 ≤ gi,ri, di ≤ 109 。

笔记

1. 首先判断能够从s点到达t点（注意：红灯时能够反向通行）也就是说，该有向图是双向的。

class GraphMatrix(object):
    """
    图的邻接矩阵
    """
    def __init__(self, kind):

        # 图的类型: 无向图, 有向图, 无向网, 有向网

        # kind: Undigraph, Digraph, Undinetwork, Dinetwork,

​        self.kind = kind

        # 顶点表

​        self.vertexs = []

        # 边表, 即邻接矩阵, 是个二维的

​        self.arcs = []

        # 当前顶点数

​        self.vexnum = 0

        # 当前边(弧)数

​        self.arcnum = 0

3.2692:质因数个数

时间限制: 2s 内存限制: 256MB 提交: 2495 解决: 352

题目描述

给定正整数 n，请问有多少个质数是 n 的约数。

输入格式

输入的第一行包含一个整数 n。

输出格式

输出一个整数，表示 n 的质数约数个数。

样例输入

396

样例输出

3

提示

396 有 2, 3, 11 三个质数约数。

对于 30% 的评测用例，1 ≤ n ≤ 10000。

对于 60% 的评测用例，1 ≤ n ≤ 109。

对于所有评测用例，1 ≤ n ≤ 1016。

思路

1. 使用循环遍历会导致时间超时，所以需要缩减遍历。例如，10的约数为1，2，5，10.当10/5时得到2，并且2<5可知，在前面已经存在10/2=5了，进而将遍历的时间缩短了一半。
2. 首先判断i是否是n的约数，，由于是从2开始的，如果能够被2除尽，则2为质因数，此时将n除2直到不能得到整数，再对i+1，依次进行循环处理。
3. 所有的整数，都可以分解为质因数相乘的结果。

代码

n = int(input())
i = 2
res = 0
while i <= n//i:
    if(n % i  == 0):
        res+=1
        while(n % i  == 0):
            n //= i
    i +=1

if n>1:
    res+=1
print(res)

4.2681: 矩形拼接

时间限制: 1s 内存限制: 512MB 提交: 235 解决: 55

题目描述

已知 3 个矩形的大小依次是 a1 × b1, a2 × b2 和 a3 × b3。用这 3 个矩形能拼出的所有多边形中，边数最少可以是多少？例如用 3 × 2 的矩形（用 A 表示）、4 × 1 的矩形（用 B 表示）和 2 × 4 的矩形（用 C 表示）可以拼出如下 4 边形。

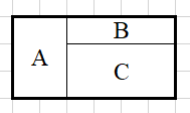
例如用 3 × 2 的矩形（用 A 表示）、3 × 1 的矩形（用 B 表示）和 1 × 1 的矩形（用 C 表示）可以拼出如下 6 边形。

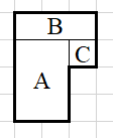
输入格式

输入包含多组数据。

第一行包含一个整数 T，代表数据组数。

以下 T 行，每行包含 6 个整数 a1, b1, a2, b2, a3, b3，其中 a1, b1 是第一个矩形的边长，a2, b2 是第二个矩形的边长，a3, b3 是第三个矩形的边长。

输出格式

对于每组数据，输出一个整数代表答案。

样例输入

2
2 3 4 1 2 4
1 2 3 4 5 6

样例输出

4
6

提示

对于 10% 的评测用例，1 ≤ T ≤ 5，1 ≤ a1, b1, a2, b2, a3, b3 ≤ 10，a1 = a2 = a3。

对于 30% 的评测用例，1 ≤ T ≤ 5，1 ≤ a1, b1, a2, b2, a3, b3 ≤ 10。

对于 60% 的评测用例，1 ≤ T ≤ 10，1 ≤ a1, b1, a2, b2, a3, b3 ≤ 20。

对于所有评测用例，1 ≤ T ≤ 1000，1 ≤ a1, b1, a2, b2, a3, b3 ≤ 100。

思路

1. 三个矩形叠加在一起形成的图形最少边数有三种情况，4，6，8。
2. 当a1 = a2 = a3时，可以组成的最少边数为4。
3. 进行分类匹配

代码

import os
import sys

# x1, x2, x3表示分别从三个矩形中获取的边长
def check1(x1, x2, x3):  # 能完全匹配，四边形
    if x1 >= x2 and x1 >= x3:
        if x1 == x2 + x3 and a[2] + a[3] - x2 == a[4] + a[5] - x3:
            return True
    if x2 >= x1 and x2 >= x3:
        if x2 == x1 + x3 and a[0] + a[1] - x1 == a[4] + a[5] - x3:
            return True
    if x3 >= x1 and x3 >= x2:
        if x3 == x1 + x2 and a[0] + a[1] - x1 == a[2] + a[3] - x2:
            return True
    return False


def chachk2(x1, x2, x3):  # 能部分匹配，六边形
    if x1 >= x2 and x1 >= x3:
        if x1 == x2 + x3:
            return True
    if x2 >= x1 and x2 >= x3:
        if x2 == x1 + x3:
            return True
    if x3 >= x1 and x3 >= x2:
        if x3 == x1 + x2:
            return True
    return False


T = int(input())
for t in range(T):
    a = list(map(int, input().split()))
    ans = 8  # 除能完全匹配和部分匹配外的为八变形
    for i in range(0, 2):  # 第1个矩形横竖两种摆法
        for j in range(2, 4):  # 第2个矩形横竖两种摆法
            for k in range(4, 6):  # 第3个矩形横竖两种摆法
                x1, x2, x3 = a[i], a[j], a[k]
                if x1 == x2 and x2 == x3:  # 三边相等一定能拼成四边形
                    ans = min(ans, 4)
                if check1(x1, x2, x3):
                    ans = min(ans, 4)
                if x1 == x2 or x2 == x3 or x3 == x1:
                    ans = min(ans, 6)
                if chachk2(x1, x2, x3):
                    ans = min(ans, 6)
    print(ans)

5.2686: 消除游戏

时间限制: 3s 内存限制: 512MB 提交: 1109 解决: 47

题目描述

在一个字符串 S 中，如果 S i = S i−1 且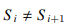，则称 S i 和 S i+1 为边缘字符。如果且 S i = S i+1，则 S i−1 和 S i 也称为边缘字符。其它的字符都不是边缘字符。

对于一个给定的串 S，一次操作可以一次性删除该串中的所有边缘字符（操作后可能产生新的边缘字符）。

请问经过 2^64 次操作后，字符串 S 变成了怎样的字符串，如果结果为空则输出 EMPTY。

输入格式

输入一行包含一个字符串 S 。

输出格式

输出一行包含一个字符串表示答案，如果结果为空则输出 EMPTY。

样例输入

edda

样例输出

EMPTY

提示

对于 25% 的评测用例，|S | ≤ 103 ，其中 |S | 表示 S 的长度；

对于 50% 的评测用例，|S | ≤ 104 ；

对于 75% 的评测用例，|S | ≤ 105 ；

对于所有评测用例，|S | ≤ 106，S 中仅含小写字母。

思路

1. 使用两个list，存储相隔距离为1的string的索引
2. 通过边缘元素的判断，得出边缘元素的索引list，
3. 遍历边缘元素的索引list，如果标记list为true，表明该元素已经remove过，否则remove该元素，并置标记list为true。
4. 输出是将元素拼接成新的string，并判断是否为空。

代码

N=10**6+10
pos=[]
l,r=[0]*N,[0]*N
st=[False]*N
s=input()
n=len(s)
s="@"+s+"@"
# 构建双向链表
for i in range(1,n+1):
    l[i]=i-1
    r[i]=i+1
# 查找所有边缘字符
# 6
def check(i):
    if s[l[i]]=="@" or s[r[i]]=="@":
        return
    if s[l[i]]==s[i] and s[r[i]]!=s[i]:
        pos.append(r[i])
        pos.append(i)
    if s[l[i]]!=s[i] and s[r[i]]==s[i]:
        pos.append(l[i])
        pos.append(i)

def remove(j):
    r[l[j]]=r[j]
    l[r[j]]=l[j]
    # 删除j结点，置为True
    st[j]=True

for i in range(1,n+1):
    check(i)
while pos:
    ne=[]
    for p in pos:
        if st[p]:continue
        remove(p)
        ne.append(l[p])
        ne.append(r[p])
    pos=[]
    for e in ne:
        if not st[e]:
            check(e)
ans=""
for i in range(1,n+1):
    if not st[i]:
        ans+=s[i]
if ans:
    print(ans)
else:
    print("EMPTY")

6.2666: 爬树的甲壳虫

题目描述

有一只甲壳虫想要爬上一颗高度为 n 的树，它一开始位于树根，高度为 0，当它尝试从高度 i − 1 爬到高度为 i 的位置时有 Pi 的概率会掉回树根，求它从树根爬到树顶时，经过的时间的期望值是多少。

输入格式

输入第一行包含一个整数 n 表示树的高度。

接下来 n 行每行包含两个整数 xi , yi，用一个空格分隔，表示。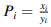

输出格式

输出一行包含一个整数表示答案，答案是一个有理数，请输出答案对质数 998244353 取模的结果。其中有理数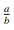对质数 P 取模的结果是整数 c 满足 0 ≤ c < P 且 c · b ≡ a (mod P)。

样例输入

1
1 2

样例输出

2

提示

对于 20% 的评测用例，n ≤ 2，1 ≤ xi < yi ≤ 20 ；

对于 50% 的评测用例，n ≤ 500，1 ≤ xi < yi ≤ 200 ；

对于所有评测用例，1 ≤ n ≤ 100000，1 ≤ xi < yi ≤ 109 。

思路

代码

mod = 998244353
n = int(input())
# E[0] = 0
result = 0
for _ in range(n):
    x, y = map(int, input().split())
    result = (result + 1) * y % mod * \
             pow(y - x, mod - 2, mod) % mod
print(result)

7.2688:技能升级

时间限制: 1s 内存限制: 512MB 提交: 1107 解决: 90

题目描述

小蓝最近正在玩一款 RPG 游戏。他的角色一共有 N 个可以加攻击力的技能。其中第 i 个技能首次升级可以提升 Ai 点攻击力，以后每次升级增加的点数都会减少 Bi。(上取整) 次之后，再升级该技能将不会改变攻击力。

现在小蓝可以总计升级 M 次技能，他可以任意选择升级的技能和次数。请你计算小蓝最多可以提高多少点攻击力？

输入格式

输入第一行包含两个整数 N 和 M。

以下 N 行每行包含两个整数 Ai 和 Bi。

输出格式

输出一行包含一个整数表示答案。

样例输入

3 6
10 5
9 2
8 1

样例输出

47

提示

对于 40% 的评测用例，1 ≤ N, M ≤ 1000；

对于 60% 的评测用例，1 ≤ N ≤ 104 , 1 ≤ M ≤ 107；

对于所有评测用例，1 ≤ N ≤ 105，1 ≤ M ≤ 2 × 109，1 ≤ Ai , Bi ≤ 106。

代码

import math
N,M = map(int,input().split())
a_list = [0]
b_list = [0]
c_list = [0]
for _ in range(N):
    a,b = map(int,input().split())
    c = math.ceil(a/b)
    a_list.append(a)
    b_list.append(b)
    c_list.append(c)

ans = 0
for i in range(M):
    temp = max(a_list)
    if temp>0:
        idx = a_list.index(temp)
        ans +=temp
        a_list[idx] = temp - b_list[idx]
    else:
        break
print(ans)

代码-二分

import os
import sys

# 请在此输入您的代码
def check(mid):
    cnt = 0
    for i in range(n):
        if a[i] < mid:
            continue
        cnt += (a[i] - mid) // b[i] + 1
        if cnt >= m:
            return True
    return False


n, m = map(int, input().split())
a = []
b = []
for _ in range(n):
    a1, b1 = map(int, input().split())
    a.append(a1)
    b.append(b1)
l, r = 1, 1000000
while l <= r:
    mi = (l + r) // 2
    if check(mi):
        l = mi + 1
    else:
        r = mi - 1
attack = 0
res = m
for i in range(n):
    if a[i] < r:
        continue
    t = (a[i] - l) // b[i] + 1
    if a[i] - b[i] * (t - 1) == r:
        t -= 1
    attack += (a[i] * 2 - (t - 1) * b[i]) * t / 2
    res -= t
print(int(attack) + res * r)

8.2583: 单词分析

时间限制: 1s 内存限制: 128MB 提交: 1236 解决: 596

题目描述

小蓝正在学习一门神奇的语言，这门语言中的单词都是由小写英文字母组成，有些单词很长，远远超过正常英文单词的长度。小蓝学了很长时间也记不住一些单词，他准备不再完全记忆这些单词，而是根据单词中哪个字母出现得最多来分辨单词。
现在，请你帮助小蓝，给了一个单词后，帮助他找到出现最多的字母和这个字母出现的次数。

输入格式

输入一行包含一个单词，单词只由小写英文字母组成。

输出格式

输出两行，第一行包含一个英文字母，表示单词中出现得最多的字母是哪个。如果有多个字母出现的次数相等，输出字典序最小的那个。
第二行包含一个整数，表示出现得最多的那个字母在单词中出现的次数。

样例输入

lanqiao

样例输出

a
2

提示

对于所有的评测用例，输入的单词长度不超过 1000。

思路

1. 暴力求解
2. 计数和字母需要单独求解，需要两个循环，不能一起得到

代码

word=input()
a=0
b=[]
for i in word:
    c=word.count(i)
    if c>=a:
        a=c
for j in word:
    if word.count(j)==a:
        b.append(j)
b.sort()
print(b[0])
print(a)

9.2591: 成绩统计

时间限制: 1s 内存限制: 128MB 提交: 1435 解决: 743

题目描述

小蓝给学生们组织了一场考试，卷面总分为100分，每个学生的得分都是一个0到100的整数。如果得分至少是 60分，则称为及格。如果得分至少为85分，则称为优秀。
请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整数。

输入格式

输入的第一行包含一个整数n，表示考试人数。接下来 n行，每行包含一个 0至 100的整数，表示一个学生的得分。

输出格式

输出两行，每行一个百分数，分别表示及格率和优秀率。百分号前的部分四舍五入保留整数。

样例输入

7
80
92
56
74
88
100
0

样例输出

71%
43%

代码

n=int(input())
a=[int(input()) for i in range(n)]
def f(x):
    return format(100*len([i for i in a if i>=x])/n,'.0f')+'%'
print(f(60),f(85),sep='\n')

10. 2571: 回文日期

时间限制: 1s 内存限制: 128MB 提交: 4012 解决: 1015

题目描述

2020 年春节期间，有一个特殊的日期引起了大家的注意：2020年2月2日。因为如果将这个日期按“yyyymmdd” 的格式写成一个8 位数是20200202，
恰好是一个回文数。我们称这样的日期是回文日期。
有人表示20200202 是“千年一遇” 的特殊日子。对此小明很不认同，因为不到2年之后就是下一个回文日期：20211202 即2021年12月2日。
也有人表示20200202 并不仅仅是一个回文日期，还是一个ABABBABA型的回文日期。对此小明也不认同，因为大约100 年后就能遇到下一个ABABBABA 型的回文日期：21211212 即2121 年12 月12 日。算不上“千年一遇”，顶多算“千年两遇”。
给定一个8 位数的日期，请你计算该日期之后下一个回文日期和下一个ABABBABA型的回文日期各是哪一天。

输入格式

输入包含一个八位整数N，表示日期。

输出格式

输出两行，每行1 个八位数。第一行表示下一个回文日期，第二行表示下
一个ABABBABA 型的回文日期。

样例输入

20200202

样例输出

20211202
21211212

提示

对于所有评测用例，10000101 ≤ N ≤ 89991231，保证N 是一个合法日期的8位数表示。

思路

1. 将输入的日期进行拆分，年，月，日
2. 先将年份加一，然后revese进行判断是否符合月日标准，这是第一个回文日期
3. 将年份计算之后，使用datetime的转换方法判断是否属于日期
4. 设计依次加一的方式进行判断

代码

import datetime
N = input()
Long = 89991231

def huiwen(N):
    if N[3] == N[4]:
        if N[2] == N[5]:
            if N[1] == N[6]:
                if N[0] == N[7]:
                    return True
    else:
        return False
    return False
def AB(N):
    if N[0] == N[2]:
        if N[1] == N[3]:
            return True
        else:
            return False
    else:
        return False

def isdate(N):
    try:
        N = datetime.datetime.strptime(N,"%Y%m%d")
        return True
    except Exception as e:
        if e != "":
            return False
        else:
            return True


date = list(N)
dateNum = [int(x) for x in date]

huiwenNum =abNum =0
for i in range(10000):
    sign_one = sign_hundred = sign_thousand = 0
    dateNum[3] = dateNum[3]+1
    sign_one = int(dateNum[3]/10)
    dateNum[3] %= 10
    dateNum[4] = dateNum[3]
    if sign_one ==1:
        dateNum[2] += 1
        sign_hundred = int(dateNum[2] / 10)
        dateNum[2] %= 10
    dateNum[5] = dateNum[2]
    if sign_hundred ==1:
        dateNum[1] += 1
        sign_thousand = int(dateNum[1] / 10)
        dateNum[1] %= 10
    dateNum[6] = dateNum[1]
    if sign_thousand ==1:
        dateNum[0] += 1
        dateNum[0] %= 10
    dateNum[7] = dateNum[0]

    dateStr = [str(x) for x in dateNum]
    dateStr = "".join(dateStr)
    if isdate(dateStr):
        # 判读是日期是否属于回文
        if huiwen(dateNum):
            if huiwenNum ==0:
                print(dateStr)
                huiwenNum+=1
        if AB(dateNum):
            if abNum ==0:
                print(dateStr)
            break
    else:
        continue

11.数字三角形

题目描述

上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右 边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

输入描述

输入的第一行包含一个整数 N\ (1 \leq N \leq 100)N (1≤N≤100)，表示三角形的行数。

下面的 NN 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。

输出描述

输出一个整数，表示答案。

输入输出样例

示例

输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

输出

27

思路

1. 从上到下依次进行计算
2. 在计算时将该元素直接更换成相加的结果
3. 最后返回时一定是在中间，题目规定向左和向右步数相差不能大于1

代码

h = int(input())  # 输入数据
W = [list(map(int, input().split())) for i in range(h)]
# 循环遍历计算到每一行的和的最大值
for i in range(1, h):
    for j in range(0, i + 1):
        if j == 0:  # 最左边元素只能由右上方得到
            W[i][j] += W[i - 1][j]
        elif j == i:  # 最右边元素只能由左上方得到
            W[i][j] += W[i - 1][j - 1]
        else:  # 其余元素由上方较大值得到
            W[i][j] += max(W[i - 1][j - 1: j + 1])
if h & 1:  # 如果是奇数行，则返回最中间值
    print(W[-1][h // 2])
else:  # 偶数行则返回中间较大值
    print(max(W[-1][h // 2 - 1], W[-1][h // 2]))

12.成绩分析

题目描述

小蓝给学生们组织了一场考试，卷面总分为 100 分，每个学生的得分都是一个 0 到 100 的整数。

请计算这次考试的最高分、最低分和平均分。

输入描述

输入的第一行包含一个整数 n\ (1 ≤ n ≤ 10^4)n (1≤n≤104)，表示考试人数。

接下来 nn 行，每行包含一个 0 至 100 的整数，表示一个学生的得分。

输出描述

输出三行。

第一行包含一个整数，表示最高分。

第二行包含一个整数，表示最低分。

第三行包含一个实数，四舍五入保留正好两位小数，表示平均分。

输入输出样例

示例

输入

7
80
92
56
74
88
99
10

输出

99
10
71.29

代码

n=int(input())
lis=list()
for i in range(n):
  lis.append(int(input()))

print(max(lis))
print(min(lis))
print("{:.2f}".format(sum(lis)/n))

13.货物摆放

题目描述

小蓝有一个超大的仓库，可以摆放很多货物。

现在，小蓝有 nn 箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、宽、高。

小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 LL、WW、HH 的货物,满足 n = L \times W \times Hn=L×W×H。

给定 nn，请问有多少种堆放货物的方案满足要求。

例如，当 n = 4n=4 时，有以下 66 种方案：1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 × 1 × 11×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1。

请问，当 n = 2021041820210418n=2021041820210418 （注意有 1616 位数字）时，总共有多少种方案？

提示：建议使用计算机编程解决问题。

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

代码

# 三个数字相乘等于 2021041820210418

n=2021041820210418
l=[]     # ！！！！用于存因数不是因子例如：10=2*5
i=2
x=n
# 通过开根号 并且存在能够除尽的数，将x存入l中
while i<pow(x+1,0.5):
    if x%i==0:
        l.append(i)
        x=x//i
    else:
        i+=1
l.append(x)
# 设置一个集合
s=set()     # ！！！！用于存因子 如10=1*2*5*10
s.add(1)
for j in l:
    p=set()
    for k in s:
        p.add(j*k)
    for k in p:
        s.add(k)
count=0
for k1 in s:             # 遍历两层求解
    for k2 in s:
        if n%(k1*k2)==0:
            count+=1
print(count)

14.等差素数列

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

2,3,5,7,11,13,....2,3,5,7,11,13,.... 是素数序列。 类似：7,37,67,97,127,1577,37,67,97,127,157 这样完全由素数组成的等差数列，叫等差素数数列。

上边的数列公差为 3030，长度为 66。

20042004 年，格林与华人陶哲轩合作证明了：存在任意长度的素数等差数列。 这是数论领域一项惊人的成果！

有这一理论为基础，请你借助手中的计算机，满怀信心地搜索：

长度为 10 的等差素数列，其公差最小值是多少？

思路

若公差不是2的倍数，那么长度为10的等差数列里，必有一个2的倍数。所以，公差必须是2的倍数。同理，公差必须是3、5、7的倍数，所以求2、3、5、7的最小公倍数即可。而正因为2、3、5、7都是素数，所以它们的最小公倍数就是它们的积。

代码

print(2*3*5*7)

15.杨辉三角形

题目描述

下面的图形是著名的杨辉三角形：

如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列： 1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1。....

给定一个正整数 N，请你输出数列中第一次出现 N 是在第几个数？

输入描述

输入一个整数 N。

输出描述

输出一个整数代表答案。

输入输出样例

示例 1

输入

6

输出

13

评测用例规模与约定

对于 20% 的评测用例，1≤N≤10； 对于所有评测用例，1≤N≤1000000000。

思路

1. 不可以使用二叉树的数据排列方式进行计算
2. 只需看左半边，并且斜着看是递增序列，横着看是严格递增序列，因此只会在靠近三角形内部的斜行中出现，不会再外面的斜行中出现
3. 从内向外搜索

代码

def C(n, m):
  up = 1; down = 1
  t = n
  for i in range(1, min(m, n - m) + 1):
    up *= t; t -= 1
    down *= i
  return up // down

n = int(input())

def search(i):
  l = i; r = max(n, l); k = i // 2
  while l < r:
    mid = l + r >> 1
    if C(mid, k) < n: l = mid + 1
    else: r = mid
  return l

for i in range(34, -1, -2):
  t = search(i)
  if C(t, i // 2) == n:
    print(t * (t + 1) // 2 + i // 2 + 1)
    break

16. 跳跃

题目描述

小蓝在一个 n 行 m 列的方格图中玩一个游戏。

开始时，小蓝站在方格图的左上角，即第 1 行第 1 列。

小蓝可以在方格图上走动，走动时，如果当前在第 r 行第 c 列，他不能走到行号比r 小的行，也不能走到列号比 c* 小的列。同时，他一步走的直线距离不超过3。

例如，如果当前小蓝在第 3 行第 5 列，他下一步可以走到第 3 行第 6 列、第 3 行第 7 列、第 3 行第 8 列、第 4 行第 5 列、第 4 行第 6 列、第 4 行第 7 列、第 5 行第 5 列、第 5 行第 6 列、第 6 行第 5 列之一。

小蓝最终要走到第 n 行第m 列。

在图中，有的位置有奖励，走上去即可获得，有的位置有惩罚，走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值，奖励为正，惩罚为负。

小蓝希望，从第 1 行第 1 列走到第n 行第 m 列后，总的权值和最大。请问最大是多少？

输入描述

输入的第一行包含两个整数 n,m，表示图的大小。

接下来 n 行，每行 m 个整数，表示方格图中每个点的权值。

其中，1≤n≤100，−104≤权值≤104。

输出描述

输出一个整数，表示最大权值和。

输入输出样例

示例 1

输入

3 5
-4 -5 -10 -3 1
7 5 -9 3 -10
10 -2 6 -10 -4

输出

15

思路

1. 使用逆向思维，不采用从（0，0）开始向右向下遍历，采用向左向上进行遍历。如果出现负数则跳过。
2. 在进行遍历的时候，将数据进行更新表明从前方到该点的最大代价

代码

n, m = map(int, input().split())
dp = [[*map(int, input().split())] for _ in range(n)]
direct = [(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(2,0),(2,1),(3,0)]# 可能行走的距离
for x in range(n):
  for y in range(m):
    res = []
    for dx,dy in direct:
      lx = x - dx
      ly = y - dy
      if(lx>=0 and ly>=0 and lx<n and ly<m):
        res.append(dp[lx][ly])
    dp[x][y] += max(res) if len(res)!=0 else 0
print(dp[-1][-1])

17.时间显示

题目描述

小蓝要和朋友合作开发一个时间显示的网站。

在服务器上，朋友已经获取了当前的时间，用一个整数表示，值为从 1970 年 11 月 11 日 00:00:00 到当前时刻经过的毫秒数。

现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需要显示出时分秒即可，毫秒也不用显示，直接舍去即可。

给定一个用整数表示的时间，请将这个时间对应的时分秒输出。

输入描述

输入一行包含一个整数，表示时间。

输出描述

输出时分秒表示的当前时间，格式形如 HH:MM:SS，其中 HH 表示时，值为 00 到 23，MM 表示分，值为 00 到 59，SS 表示秒，值为 00 到 59。时、分、秒 不足两位时补前导 00。

输入输出样例

示例 1

输入

46800999

输出

13:00:00

示例 2

输入

1618708103123

输出

01:08:23

评测用例规模与约定

对于所有评测用例，给定的时间为不超过 10的18次方的正整数。

代码

from datetime import datetime, timedelta

start = datetime(year=1970, month=1, day=1)
dela = timedelta(milliseconds=1)
now = int(input())

now = start + now * dela
print('%02d:%02d:%02d' % (now.hour, now.minute, now.second))

18. 特别数的和

题目描述

小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导 0），在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。

请问，在 1 到 n* 中，所有这样的数的和是多少？

输入描述

输入一行包含一个整数 n（1≤n≤10的4次方 ）。

输出描述

输出一行，包含一个整数，表示满足条件的数的和。

输入输出样例

示例

输入

40

输出

574

代码

n = int(input())

sum = 0
for i in range(1, n + 1):
    for j in str(i):
        if j in '2019':
            sum += i
            break

print(sum)

19.子串分值

题目描述

对于一个字符串 SS，我们定义 SS 的分值 f(S)f(S) 为 SS 中恰好出现一次的字符个数。例如 f(aba) = 1，f(abc) = 3, f(aaa) = 0，f(aba)=1，f(abc)=3, f(aaa)=0。

现在给定一个字符串 S_{0 …… n − 1}S0⋯n−1（长度为 nn，1≤n≤105），请你计算对于所有 S 的非空子串 S_{i …… j}(0 ≤ i ≤ j < n)S**i⋯j(0≤i≤j<n)，f(S_{i …… j})f(S**i⋯j) 的和是多少。

输入描述

输入一行包含一个由小写字母组成的字符串 SS。

输出描述

输出一个整数表示答案。

输入输出样例

示例

输入

ababc

输出

21

思路

这道题可以用暴力解法，但是本题的本意并不是在这里。

这里其实是求字母的贡献度，只有当字母个数在子串中个数为1才会有贡献度。

对此，我们可以从要分析字母A的左右两边出发，分别计算移动了多远才会出现一个字母与A相同，然后停止遍历，记录下步长left和right。

然后是怎么算总的贡献度。 当前字母的贡献度=(left+1) * (right+1)。

为什么是这个呢？ 以bacbacdb为例,我们对第四个字母b进行分析:

• 先往左边遍历,可以移动两个单位,则left = 2;
• 再往右边遍历,可以移动3个单位,则right = 3;
• 则对于b字母,有贡献度的部分为acbacd,满足的字串(注意要有b)有：
• 从左边第一个字母a开始,分别是acb,acba,acbac,acbacd,有4个
• 然后左边从第二个字母c开始,为cb,cba,cbac,cbacd,有4个
• 从左边第三个字母b开始,为b,ba,bac,bacd,有4个
• 我们在分析过程中可以得到规律,就是(往左移动的步数+1) * (往右移动的步数+1),加1是因为要包含分析的字母

代码

S = input()  #输入字符串
sumvalue =0
#遍历计算一个字符的贡献值，
for i in range(0,len(S)):
  numleft =0
  numright = 0
  temp = S[i] #也就是第i个字符的
  loc = i-1
  while(loc>=0 and S[loc]!=temp):
    loc-=1
    numleft+=1
  loc = i+1
  while(loc<len(S) and S[loc]!=temp):
    loc+=1 #一直往上加
    numright+=1
  sumvalue+=((numleft+1)*(numright+1)) #也就是
  # print(numleft,numright)
  # print(((numleft+1)*(numright+1)))
print(sumvalue)