基于全阶观测器的三自由度运动系统状态反馈控制simulink建模与仿真

1.课题概述

       基于全阶观测器的三自由度运动系统状态反馈控制simulink建模与仿真。整个控制系统包含闭环结构，全阶观测器，三自由度车辆模型。

 

2.系统仿真结果

（完整程序运行后无水印）

 

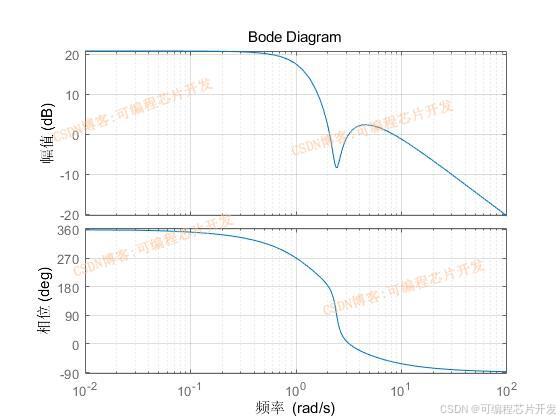
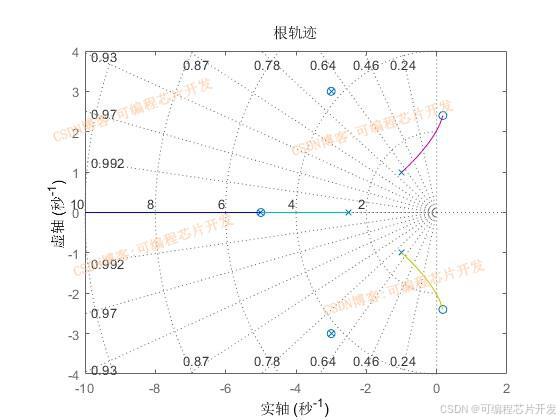
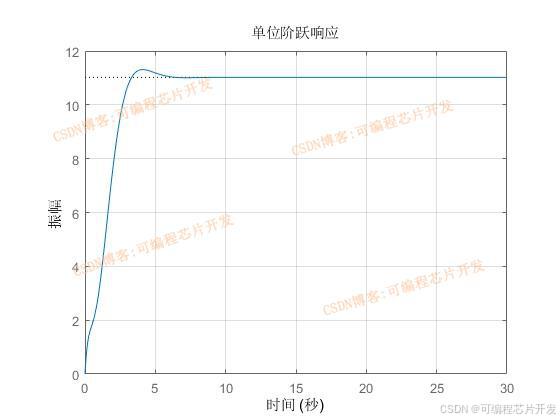
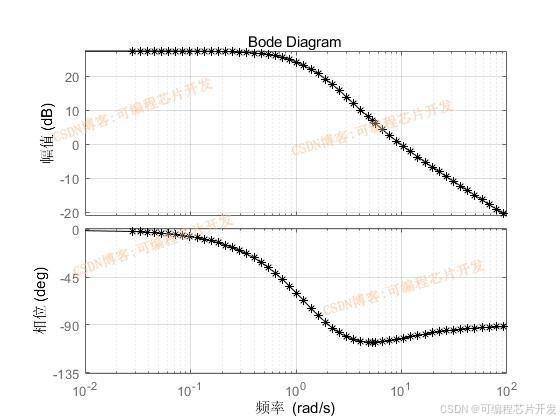
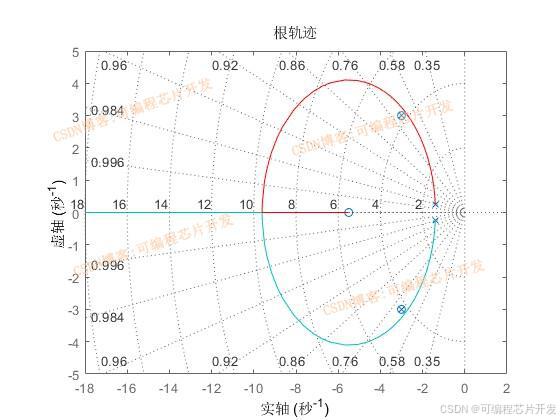
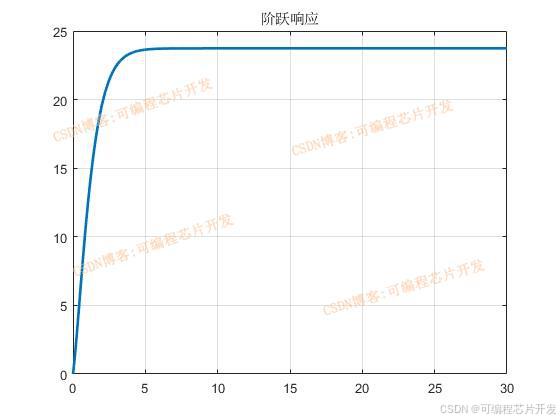
3.核心程序与模型

版本：MATLAB2022a

%反馈,计算反馈向量
K         = place(A,B,sys_pole);							
vector_fb = acker(A',C',view_pole);
vector_fb = vector_fb';
fprintf('反馈向量:\n\n');
vector_fb


%分析观测器模型
AHC       = A - vector_fb*C;
fprintf('观测器矩阵:\n\n');
AHC

%全阶观测器
Rk = rank(A);
A2 = [A-B*K    ,B*K;
zeros(Rk),A-vector_fb*C];

[nb1,nb2] = size(B);

B2        = [B;zeros(Rk,nb2)];						
C2        = [C zeros(nb2,Rk)];		
D2        = D;
[num,den] = ss2tf(A2,B2,C2,D2,1);

figure;
bode(num,den,'k-*');
grid on;		

%分析观测器的根轨迹
figure;
rlocus(num,den);
grid on;					


%闭环零极点
[Z,P,K]=tf2zp(num,den);	
fprintf('零极点:\n\n');
Z
P
K
[Y,T,X] = step(num,den,30);
figure;
plot(X,Y,'linewidth',2);								
title('阶跃响应');
grid on;

%仿真三个方向的三自由度结果图
c1=[1;2;3];				
c2=[-1;-2;-3];				
syms s;
AHC=[  -0.4000  0   -5.4764
    1.0000      0   -4.6762
   -1.4000    9.8000   -9.6000];
x=ilaplace(inv(s*eye(3)-AHC))*(c1-c2);

t=0:0.01:10;
Y = double(vpa(subs(x)));

figure;
subplot(311);
plot(t,Y(1,:),'linewidth',2);
grid on
xlabel('Time(sec)');
ylabel('x方向');
subplot(312);
plot(t,Y(2,:),'linewidth',2);
grid on
xlabel('Time(sec)');
ylabel('y方向');
subplot(313);
plot(t,Y(3,:),'linewidth',2);
grid on
xlabel('Time(sec)');
ylabel('z方向');

　　

 

4.系统原理简介

       全阶观测器在控制工程中扮演着关键角色，特别是在实现状态反馈控制的复杂系统中，例如三自由度运动系统。这类系统广泛应用于航天器姿态控制、机器人臂操纵等领域，要求高度的稳定性和精度。

 

      首先，我们定义一个简化的三自由度运动系统模型，假设系统遵循线性动力学方程，忽略非线性效应和外部扰动。设系统状态向量为x(t)=[x1​,x2​,x3​]T，表示三个自由度的角位置或角速度（具体根据系统定义），系统的动力学可以用状态空间形式表示为：

 

 

 

       基于全阶观测器的三自由度运动系统状态反馈控制策略，通过精准的状态估计和设计合理的控制律，实现了对复杂动态系统的高效控制。该方法不仅提高了系统的稳定性和响应速度，还增强了对外界干扰的抵抗能力，是现代控制理论在高精度运动控制领域的重要应用。