基于遗传优化模糊控制器的水箱水位控制系统simulink建模与仿真

1.课题概述

       基于遗传优化模糊控制器的水箱水位控制系统simulink建模与仿真。对比模糊控制器和基于遗传优化的模糊控制器。

 

2.系统仿真结果

遗传算法迭代过程：

 

 

 

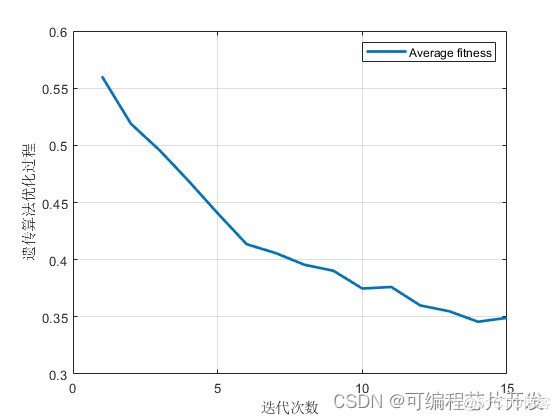
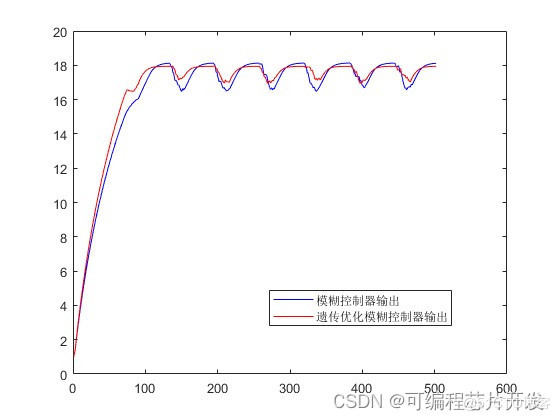
遗传优化模糊控制和模糊控制的控制器输出对比：

 

 

 

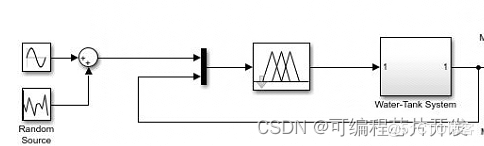
3.核心程序与模型

版本：MATLAB2022a

 

matlab部分：

Areas = [];
% FIS = addvar(FIS,'input','Cost',[0.5 1.5]);
Areas = [Areas,[0.4;0.6]];
Areas = [Areas,[1.2;1.8]];


%FIS = addmf(FIS,'input',1,'Cheap','trimf', [0 0.5 0.75]);
Areas = [Areas,[0.4;0.6]];
Areas = [Areas,[0.6;0.9]];

%FIS = addmf(FIS,'input',1,'Expensive','trimf',[1.25 1.5 2]);
Areas = [Areas,[1.2;1.3]];
Areas = [Areas,[1.4;1.6]];
Areas = [Areas,[1.8;2.2]];

%FIS = addmf(FIS,'input',1,'Medium','trapmf',[0.5 0.75 1.25 1.5]);
Areas = [Areas,[0.4;0.6]];
Areas = [Areas,[0.6;0.9]];
Areas = [Areas,[1.2;1.3]];
Areas = [Areas,[1.4;1.6]];

%FIS = addvar(FIS,'input','Water level prev',[5 20]);
Areas = [Areas,[4;6]];
Areas = [Areas,[15;25]];
....................................................................



FieldD = [rep([10],[1,Nums]);Areas;rep([0;0;0;0],[1,Nums])];

gen   = 0;
Js    = 0.5*rand(NIND,1);
Objv  = (Js+eps);
gen   = 0; 



while gen < MAXGEN

      Pe0 = 0.99;
      pe1 = 0.01; 

FitnV=ranking(Objv);    
      Selch=select('sus',Chrom,FitnV);    
      Selch=recombin('xovsp', Selch,Pe0);   
      Selch=mut( Selch,pe1);   
      phen1=bs2rv(Selch,FieldD);   

      for jj=1:1:NIND
          [gen,jj]
          X           = phen1(jj,:);
          %计算对应的目标值
          [FIS2]      = func_obj(X);
          sim("GA_opt")% Simulink模型"tops"。
          load y2.mat
dat = ans.Data;
len = length(dat);
          E           = std(dat(len/2:len,2));
JJ(jj,1)     = E;
      end 

Objvsel=(JJ);    
      [Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);   
      gen=gen+1; 


      Error2(gen) = mean(JJ);
end 
Error2=smooth(Error2,4);
figure
plot(Error2,'linewidth',2);
grid on
xlabel('迭代次数');
ylabel('遗传算法优化过程');
legend('Average fitness');



[V,I] = min(JJ);
X     = phen1(I,:);


.............................................................................
% 将规则列表添加到FIS中。
FIS2 = addrule(FIS, ruleList);


sim("GA_opt2")

save y3GA.mat Error2 X
54

　　

 

simulink部分：

 

4.系统原理简介

       基于遗传优化模糊控制器的水箱水位控制系统是一种将模糊控制与遗传算法相结合的智能控制策略，旨在实现水箱水位的精确控制。模糊控制利用模糊逻辑处理不精确或不确定的信息，而遗传算法则作为一种全局优化技术，用于自动调整模糊控制器的参数，提高控制性能。

 

4.1 模糊控制器原理

      模糊控制基于模糊集合理论，用于处理具有语言描述而非精确数值的控制问题。对于水箱水位控制系统，模糊控制器的主要组成部分包括：

 

输入变量：水箱当前水位（Error, e）和水位变化率（Change of Error, ce）。

输出变量：阀门开度控制信号（Control, u）。

 

 

 

4.2 遗传算法原理

       遗传算法（Genetic Algorithm, GA）是一种模拟自然选择和遗传机制的优化算法，用于搜索模糊控制器的最优参数集，如模糊规则的隶属度函数参数、权重因子等。

 

编码

首先，将模糊控制器的参数编码成染色体，例如使用二进制编码或实数编码。

 

选择（Selection）

基于适应度函数选择个体进行繁殖，适应度函数衡量个体（即一组参数）控制性能的好坏。

 

交叉（Crossover）

随机选取两个父代染色体，按一定概率交换部分基因片段，生成子代。

 

变异（Mutation）

以小概率改变染色体上的某些基因值，增加种群多样性。

 

重复

经过选择、交叉、变异等操作，生成新一代种群，直到满足停止条件（如最大迭代次数或达到预定的适应度阈值）。

 

4.3 遗传优化模糊控制器的工作流程

初始化：随机生成初始模糊控制器参数集，用于优化模糊控制器的隶属函数的参数，构成初始种群。

评估：应用这些参数至模糊控制器模型，通过仿真评估其控制水箱水位的效果，计算适应度值。

遗传操作：基于适应度值，进行选择、交叉、变异操作，生成新一代种群。

优化迭代：重复步骤2和3，直至达到预设的迭代次数或满足收敛条件。

结果应用：选择适应度最高的个体对应的参数，作为最终的模糊控制器参数设置，实现水箱水位的优化控制。