基于WOA鲸鱼优化的购售电收益与风险评估算法matlab仿真

1.课题概述

       基于WOA鲸鱼优化的购售电收益与风险评估算法.WOA优化算法是一种基于鲸鱼捕食过程的仿生优化算法，其包括鲸鱼行走觅食、鲸鱼包围以及鲸鱼螺旋捕食三个步骤。在WOA优化算法中，将售电公司的购售电收益风险计算公式作为WOA优化算法的目标函数，然后通过WOA的迭代优化计算售电公司的最优购电策略。最后，通过MATLAB仿真工具对本文所研究的基于WOA优化的新型购售电收益计算方法进行了仿真分析。仿真结论验证了通过WOA优化算法得到的购电策略为最优购电策略。

 

2.系统仿真结果

 

 

 

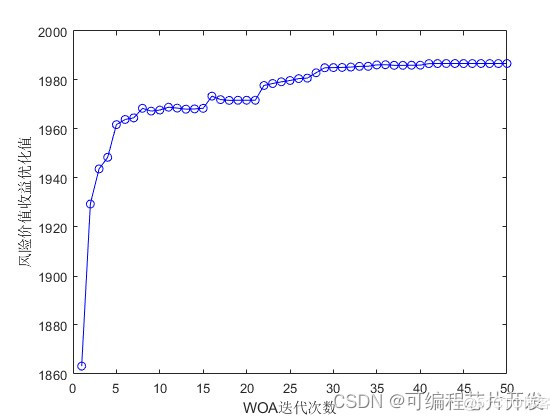
       随着WOA优化算法的不断迭代，当迭代次数大于10时，风险价值收益优化值达到最大值1715.1万元。

 

 

 

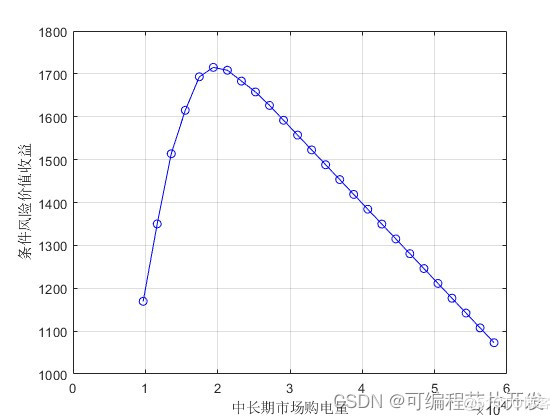
        WOA优化算法得到中长期市场购电量19405.19/ (MW·h)其对应的购售电公司的条件风险价值收益最大，而长期市场购电量小于或者大于19405.19/ (MW·h)时，其对应的条件风险价值收益均较低。

 

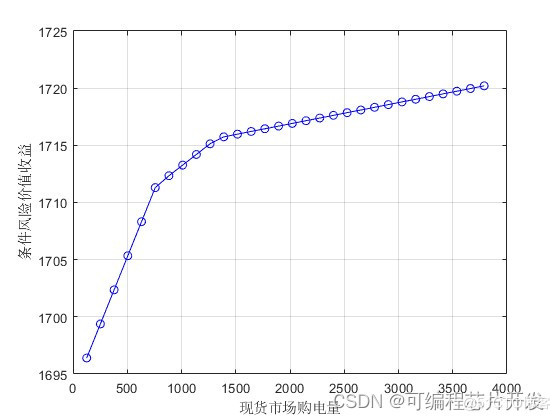
          WOA优化算法得到现货市场购电量1263.2/ (MW·h)是一个较优值，因为当现货市场购电量小于1263.2该值时，条件风险价值收益快速下降，而现货市场购电量大于1263.2时，条件风险价值收益增长非常缓慢，而现货市场购电量均有各种不稳定性因素，因此WOA优化算法得到的1263.2/ (MW·h)是一个最优值。

 

 

 

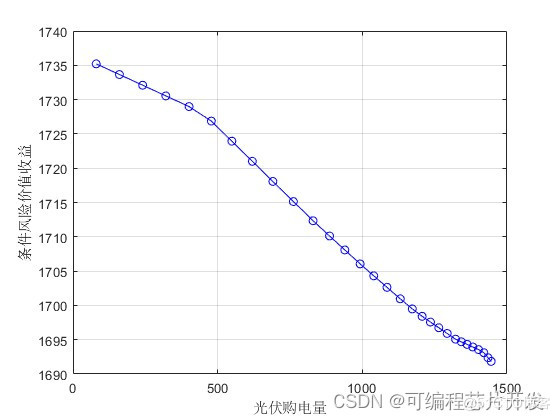
        WOA优化算法得到风电购电量1077.12/ (MW·h)，光伏购电量761.68/ (MW·h)是一个较优值。首先，当风电购电量大于1077.12/ (MW·h)时，条件风险价值收益快速下降，而小于该值时，条件风险价值收益下降较慢，同理，对于光伏发电也具有类似的趋势。

 

 

 

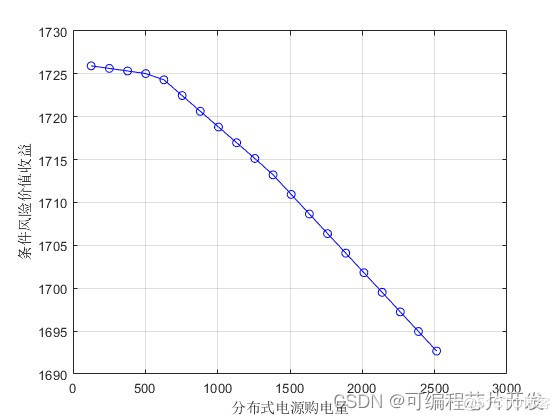
       WOA优化算法得到分布式电源购电量1256.69/ (MW·h)是一个较优值，而且由于分布式电源价格较低，因此需要购买一定的电量。

 

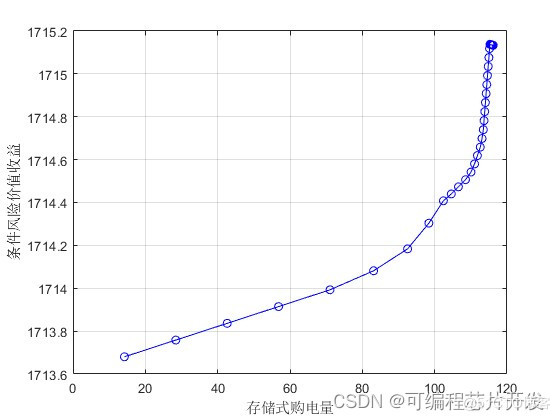
      WOA优化算法得到存储式购电量116/(MW·h)是一个较优值，因为当存储式购电量小该值时，条件风险价值收益快速下慢，而现货市场购电量大于该值时，条件风险价值收益快速增长。

 

3.核心程序与模型

版本：MATLAB2022a

for t=1:Iters
    t
    for i=1:Num
        %目标函数更新
        [pa(i),BUY]  = fitness(xwoa(i,:));
        Fitout   = pa(i);
        %更新
        if Fitout > woa_get  
            woa_get = Fitout; 
            woa_idx = xwoa(i,:);
        end
    end
    %调整参数
    c1 = 2-t*((1)/Iters); 
    c2 =-1+t*((-1)/Iters);
%     w  = 0.1+0.8*(cos(std(pa)));
    %位置更新
    for i=1:Num
        r1         = rand();
        r2         = rand();
        K1         = 2*c1*r1-c1;  
        K2         = 2*r2;             
        l          =(c2-1)*rand + 1;  
        rand_flag  = rand();   

        if rand_flag<0.5   
           if abs(K1)>=1
              RLidx    = floor(Num*rand()+1);
              X_rand   = xwoa(RLidx, :);
              D_X_rand = abs(K2*X_rand(1:D)-xwoa(i,1:D)); 
              xwoa(i,1:D)= X_rand(1:D)-K1*D_X_rand;     
           else
              D_Leader = abs(K2*woa_idx(1:D)-xwoa(i,1:D)); 
              xwoa(i,1:D)= woa_idx(1:D)-K1*D_Leader;    
           end
        else
            distLeader = abs(woa_idx(1:D)-xwoa(i,1:D));
            xwoa(i,1:D)  = distLeader*exp(l).*cos(l.*1*pi)+woa_idx(1:D);
        end

    end
    [pb,BUY]  = fitness(woa_idx);
    Pbest(t)  = pb;
end

figure;
plot(Pbest,'b-o');
xlabel('WOA迭代次数');
ylabel('风险价值收益优化值');
02_070m

　　

4.系统原理简介

       售电公司的购售电决策模型可以表示为如下表达式：

 

 

 

       售电公司的购售电最大收益和最小风险的优化目标函数为一个最优化问题，从其表达式可知，该优化问题是一个非线性的NP优化问题，采用传统的求解算法很难得到一个最优解。因此，本文将提出一种基于鲸鱼优化 (Whale optimization algorithm，WOA)的新型购售电最大收益和最小风险计算方法。