2020 CCF CSP-J2

------------恢复内容开始------------

1. 优秀的拆分

一般来说，一个正整数可以拆分成若干个正整数的和。

例如，1=1，10=1+2+3+41=1，10=1+2+3+4 等。

对于正整数 nn 的一种特定拆分，我们称它为“优秀的”，当且仅当在这种拆分下，nn 被分解为了若干个不同的 22 的正整数次幂。

注意，一个数 xx 能被表示成 22 的正整数次幂，当且仅当 xx 能通过正整数个 22 相乘在一起得到。

例如，10=8+2=23+2110=8+2=23+21 是一个优秀的拆分。

但是，7=4+2+1=22+21+207=4+2+1=22+21+20 就不是一个优秀的拆分，因为 11 不是 22 的正整数次幂。

现在，给定正整数 nn，你需要判断这个数的所有拆分中，是否存在优秀的拆分。

若存在，请你给出具体的拆分方案。

本题暂时采用AcWing数据。

输入格式

输入文件只有一行，一个正整数 nn，代表需要判断的数。

输出格式

如果这个数的所有拆分中，存在优秀的拆分。

那么，你需要从大到小输出这个拆分中的每一个数，相邻两个数之间用一个空格隔开。

可以证明，在规定了拆分数字的顺序后，该拆分方案是唯一的。

若不存在优秀的拆分，输出 “-1”（不包含双引号）。

数据范围

对于 20%20% 的数据，n≤10n≤10。
对于另外 20%20% 的数据，保证 nn 为奇数。
对于另外 20%20% 的数据，保证 nn 为 22 的正整数次幂。
对于 80%80% 的数据，n≤1024n≤1024。
对于 100%100% 的数据，1≤n≤1×1071≤n≤1×107。

输入样例1：6

输出样例1：4 2

 

#include <iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;

    if(n%2)
    {
        cout<<-1;
        return 0;
    }
    for(int i=23;i>=1;i--)
    {
        if(n >> i & 1)
            cout<< (1 << i) <<" ";
    }
}

2. 直播获奖NOI2130 即将举行。

为了增加观赏性，CCF 决定逐一评出每个选手的成绩，并直播即时的获奖分数线。

本次竞赛的获奖率为 w%w%，即当前排名前 w%w% 的选手的最低成绩就是即时的分数线。

更具体地，若当前已评出了 pp 个选手的成绩，则当前计划获奖人数为 max(1,⌊p×w%⌋)max(1,⌊𝑝×𝑤%⌋)，其中 w𝑤 是获奖百分比，⌊x⌋⌊𝑥⌋ 表示对 x𝑥 向下取整，max(x,y)max(𝑥,𝑦) 表示 x𝑥 和 y𝑦 中较大的数。

如有选手成绩相同，则所有成绩并列的选手都能获奖，因此实际获奖人数可能比计划中多。

作为评测组的技术人员，请你帮 CCF 写一个直播程序。

本题暂时采用AcWing数据。

输入格式

第 11 行两个正整数 n,w𝑛,𝑤。分别代表选手总数与获奖率。

第 22 行有 n𝑛 个非负整数，依次代表逐一评出的选手成绩。

输出格式

只有一行，包含 n𝑛 个非负整数，依次代表选手成绩逐一评出后，即时的获奖分数线。

相邻两个整数间用一个空格分隔。

数据范围

测试点编号	nn
1∼31∼3	=10=10
4∼64∼6	=500=500
7∼107∼10	=2000=2000
11∼1711∼17	=10000=10000
18∼2018∼20	=100000=100000

对于所有测试点，每个选手的成绩均为不超过 600600 的非负整数，获奖百分比 w𝑤 是一个正整数且 1≤w≤991≤𝑤≤99。

在计算计划获奖人数时，如用浮点类型的变量（如 C/C++中的 float、double，Pascal 中的 real、double、extended 等）存储获奖比例 w𝑤，则计算 5×60%5×60% 时的结果可能为 3.0000013.000001，也可能为 2.9999992.999999，向下取整后的结果不确定。因此，建议仅使用整型变量，以计算出准确值。

输入样例1：10 60

200 300 400 500 600 600 0 300 200 100

输出样例1：200 300 400 400 400 500 400 400 300 300

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
int n,w;
int main()
{
cin>>n>>w;

priority_queue<int> left;
priority_queue<int,vector<int>,greater<int>> right;

for(int i=1;i<=n;i++)
{
int x;cin>>x;

if(right.empty() || x>=right.top()) right.push(x);
else left.push(x);

int k = max(1,(i*w)/100);

while(right.size() > k) left.push(right.top()),right.pop();
while(right.size() < k) right.push(left.top()),left.pop();

cout<<right.top()<<" ";
}
}

 

 

 

 

4. 方格取数设有 n×m𝑛×𝑚 的方格图，每个方格中都有一个整数。

现有一只小熊，想从图的左上角走到右下角，每一步只能向上、向下或向右走一格，并且不能重复经过已经走过的方格，也不能走出边界。

小熊会取走所有经过的方格中的整数，求它能取到的整数之和的最大值。

本题暂时采用AcWing数据。

输入格式

第 11 行两个正整数 n,m𝑛,𝑚。

接下来 n𝑛 行每行 m𝑚 个整数，依次代表每个方格中的整数。

输出格式

一个整数，表示小熊能取到的整数之和的最大值。

数据范围

对于 20%20% 的数据，n,m≤5𝑛,𝑚≤5。
对于 40%40% 的数据，n,m≤50𝑛,𝑚≤50。
对于 70%70% 的数据，n,m≤300𝑛,𝑚≤300。
对于 100%100% 的数据，1≤n,m≤10001≤𝑛,𝑚≤1000。方格中整数的绝对值不超过 104104。

输入样例1：

3 4
1 -1 3 2
2 -1 4 -1
-2 2 -3 -1

输出样例1：

9

样例1解释

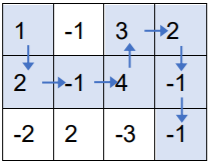
按上述走法，取到的数之和为 1+2+(−1)+4+3+2+(−1)+(−1)=91+2+(−1)+4+3+2+(−1)+(−1)=9，可以证明为最大值。

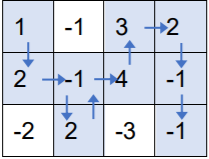
注意，上述走法是错误的，因为第 22 行第 22 列的方格走过了两次，而根据题意，不能重复经过已经走过的方格。

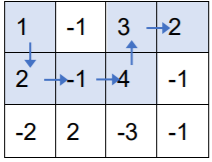
另外，上述走法也是错误的，因为没有走到右下角的终点。

输入样例2：

2 5
-1 -1 -3 -2 -7
-2 -1 -4 -1 -2

输出样例2：

-10

样例2解释

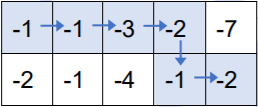
按上述走法，取到的数之和为 (−1)+(−1)+(−3)+(−2)+(−1)+(−2)=−10(−1)+(−1)+(−3)+(−2)+(−1)+(−2)=−10，可以证明为最大值。

因此，请注意，取到的数之和的最大值也可能是负数。

 

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
typedef long long ll;
ll f[N][N][2];
int g[N][N];
int main()
{
    int n,m;
    cin>>n>>m;
    
    memset(f,-0x3f,sizeof f);
    f[1][0][0] = 0;
    f[1][0][1] = 0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>g[i][j];
            
    for(int j=1;j<=m;j++)
    {
        for(int i=1;i<=n;i++)
            f[i][j][0] = max(max(f[i-1][j][0],f[i][j-1][0]),f[i][j-1][1])+g[i][j];
        
        
        for(int i=n;i;i--)
            f[i][j][1] = max(max(f[i+1][j][1],f[i][j-1][0]),f[i][j-1][1])+g[i][j];
        
    }
    
    cout<<f[n][m][0];
    
    
    
}

 

------------恢复内容结束------------