adam优化

AdaGrad (Adaptive Gradient，自适应梯度)

         对每个不同的参数调整不同的学习率，

          对频繁变化的参数以更小的步长进行更新，而稀疏的参数以更大的步长进行更新。

 

gt表示第t时间步的梯度（向量，包含各个参数对应的偏导数，gt,i表示第i个参数t时刻偏导数）

gt2表示第t时间步的梯度平方（向量，由gt各元素自己进行平方运算所得，即Element-wise）

优势：数据稀疏时，能利用稀疏梯度的信息，比标准的SGD算法更有效地收敛。

缺点：母项的对梯度平方不断累积，随之时间步地增加，分母项越来越大，最终导致学习率收缩到太小无法进行有效更新。

 

 

 

Adam更新规则

计算t时间步的梯度：

 

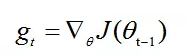
 1.计算梯度的指数移动平均数，m0 初始化为0

   β1 系数为指数衰减率，控制权重分配（动量与当前梯度），通常取接近于1的值。默认为0.9

 

2.计算梯度平方的指数移动平均数，v0初始化为0。

  β2 系数为指数衰减率，控制之前的梯度平方的影响情况。默认为0.999

  

 

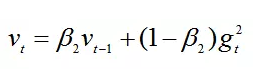
3.由于m0初始化为0，会导致mt偏向于0，对其进行纠正

  

 

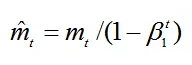
 4.v0初始化为0导致训练初始阶段vt偏向0，对其进行纠正

 

 

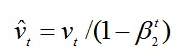
5.更新参数，其中默认学习率α=0.001ε=10^-8，避免除数变为0。

 

 6.代码

class Adam:
    def __init__(self,loss,weights,lr=0.001,beta1=0.9,beta2=0.999,epislon=1e-8):
        self.loss=loss
        self.theta=weights
        self.lr=lr
        self.beta1=beta1
        self.beta2=beta2
        self.epislon=epislon
        self.get_gradient=grad(loss)
        self.m=0
        self.v=0
        self.t=0
    def minimize_raw(self):
        self.t+=1
        g=self.get_gradient(self.theta)
        self.m=self.beta1*self.m+(1-self.beta1)*g
        self.v=self.beta2*self.v+(1-self.beta2)*(g*g)
        self.m_cat=self.m/(1-self.beta1**self.t)
        self.v_cat=self.v/(1-self.beta2**self.t)
        self.theta-=self.lr*self.m_cat/(self.v_cat**0.5+self.epislon)
        print("step{:4d}  g:{}  lr:{}  m:{}  v:{}  theta{}".format(self.t, g, self.lr, self.m, self.v, self.theta))
    def minimize(self):
        self.t+=1
        g=self.get_gradient(self.theta)
        lr=self.lr*(1-self.beta2**self.t)**0.5/(1-self.beta1**self.t)
        self.m=self.beta1*self.m+(1-self.beta1)*g
        self.v=self.beta2*self.v+(1-self.beta2)*(g*g)
        self.theta-=lr.self.m/(self.v**0.5+self.epislon)
        print("step{:4d}  g:{}  lr:{}  m:{}  v:{}  theta{}".format(self.t, g, lr, self.m, self.v, self.theta))