奇异值的物理意义第二篇
作者:阿狸
链接:https://www.zhihu.com/question/22237507/answer/119162023
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
奇异值在大部分人的印象中,往往是停留在纯粹的数学计算中。而且线性代数或者矩阵论里面,也很少讲任何跟特征值与奇异值有关的应用背景。奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是一个重要的方法。
在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction的PCA,做数据压缩(以图像压缩为代表)的算法,还有做搜索引擎语义层次检索的LSI(Latent Semantic Indexing)。
SVD的过程不是很好理解,因为它不够直观,但它对矩阵分解的效果却非常好。比如,Netflix(一个提供在线电影租赁的公司)曾经就悬赏100万美金,如果谁能提高它的电影推荐系统评分预测准确率提高10%的话。令人惊讶的是,这个目标充满了挑战,来自世界各地的团队运用了各种不同的技术。最终的获胜队伍"BellKor's Pragmatic Chaos"采用的核心算法就是基于SVD。
SVD提供了一种非常便捷的矩阵分解方式,能够发现数据中十分有意思的潜在模式。在这篇文章中,我们将会提供对SVD几何上的理解和一些简单的应用实例。首先从几何层面上去理解二维的SVD:

这就表明任意的矩阵 A 是可以分解成三个矩阵相乘的形式。V表示了原始域的标准正交基,U表示经过A 变换后的co-domain的标准正交基,Σ表示了V 中的向量与U中相对应向量之间的关系。我们仔细观察上图发现,线性变换A可以分解为旋转、缩放、旋转这三种基本线性变换。
接下来我们从分解的角度重新理解前面的表达式,我们把原来的矩阵A表达成了n个矩阵的和:
这个式子有什么用呢?注意到,我们假定是按降序排列的,它在某种程度上反映了对应项Mi在A中的“贡献”。
越大,说明对应的Mi在A的分解中占据的比重也越大。所以一个很自然的想法是,我们是不是可以提取出Mi中那些对A贡献最大的项,把它们的和作为对A的近似?
答案是肯定的,不过等一下,这个想法好像似曾相识?对了,多元统计分析中经典的主成分分析就是这样做的。在主成分分析中,我们把数据整体的变异分解成若干个主成分之和,然后保留方差最大的若干个主成分,而舍弃那些方差较小的。事实上,主成分分析就是对数据的协方差矩阵进行了类似的分解(特征值分解),但这种分解只适用于对称的矩阵,而 SVD 则是对任意大小和形状的矩阵都成立。(SVD 和特征值分解有着非常紧密的联系,此为后话)
我们再回顾一下,主成分分析有什么作用?答曰,降维。换言之,就是用几组低维的主成分来记录原始数据的大部分信息,这也可以认为是一种信息的(有损)压缩。十分赞同
的解释
一个矩阵越“奇异”,其越少的奇异值蕴含了更多的矩阵信息,矩阵的信息熵越小(这也符合我们的认知,矩阵越“奇异”,其行(或列)向量彼此越线性相关,越能彼此互相解释,矩阵所携带的信息自然也越少)。
我们用一个图像压缩的例子来说明。我们知道,电脑上的图像(特指位图)都是由像素点组成的,所以存储一张1000×622 大小的图片,实际上就是存储一个1000×622 的矩阵,共622000个元素。这个矩阵用SVD可以分解为622个矩阵之和,如果我们选取其中的前100个之和作为对图像数据的近似,那么只需要存储100个奇异值,100个
向量和 100个
向量,共计100×(1+1000+622)=162300个元素,大约只有原始的26% 大小。
我们从一个最简单的例子入手。假设我们有如下的一张 15 x 25 的图像数据:

如图所示,该图像主要由下面三部分构成

我们将图像表示成 15 x 25 的矩阵,矩阵的元素对应着图像的不同像素,如果像素是白色的话,就取 1,黑色的就取 0. 我们得到了一个具有375个元素的矩阵,如下图所示

我们可以看出矩阵的秩是3,也就是主要信息都包含在三个列向量里面,这与上面的图像由个条带组成的认知一致。如果我们对矩阵进行奇异值分解以后,得到奇异值分别是
σ1 = 14.72
σ2 = 5.22
σ3 = 3.31
矩阵A就可以表示成
vi具有15个元素,ui具有25个元素,σi对应不同的奇异值。如上图所示,我们就可以用123个元素来表示具有375个元素的图像数据了。
奇异值分解除了以上答主提到的应用以外,还有很多应用。这里在介绍两个:
1.潜在语义索引(Latent Semantic Indexing)
与PCA不太一样,至少不是实现了SVD就可以直接用的,不过LSI也是一个严重依赖于SVD的算法,之前吴军老师在矩阵计算与文本处理中的分类问题中谈到:
“三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词,其中的每个非零元素表示这类词中每个词的重要性(或者说相关性),数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章,其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。因此,我们只要对关联矩阵A进行一次奇异值分解,w 我们就可以同时完成了近义词分类和文章的分类。(同时得到每类文章和每类词的相关性)。”
上面这段话可能不太容易理解,不过这就是LSI的精髓内容,我下面举一个例子来说明一下,下面的例子来自LSA tutorial,具体的网址我将在最后的引用中给出:

这就是一个矩阵,不过不太一样的是,这里的一行表示一个词在哪些title中出现了(一行就是之前说的一维feature),一列表示一个title中有哪些词,(这个矩阵其实是我们之前说的那种一行是一个sample的形式的一种转置,这个会使得我们的左右奇异向量的意义产生变化,但是不会影响我们计算的过程)。比如说T1这个title中就有guide、investing、market、stock四个词,各出现了一次,我们将这个矩阵进行SVD,得到下面的矩阵:

左奇异向量表示词的一些特性,右奇异向量表示文档的一些特性,中间的奇异值矩阵表示左奇异向量的一行与右奇异向量的一列的重要程序,数字越大越重要。
继续看这个矩阵还可以发现一些有意思的东西,首先,左奇异向量的第一列表示每一个词的出现频繁程度,虽然不是线性的,但是可以认为是一个大概的描述,比如book是0.15对应文档中出现的2次,investing是0.74对应了文档中出现了9次,rich是0.36对应文档中出现了3次;
其次,右奇异向量中的第一行表示每一篇文档中的出现词的个数的近似,比如说,T6是0.49,出现了5个词,T2是0.22,出现了2个词。
然后我们反过头来看,我们可以将左奇异向量和右奇异向量都取后2维(之前是3维的矩阵),投影到一个平面上,可以得到:
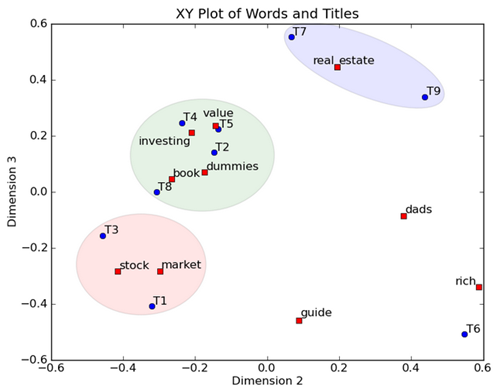 在图上,每一个红色的点,都表示一个词,每一个蓝色的点,都表示一篇文档,这样我们可以对这些词和文档进行聚类,比如说stock 和 market可以放在一类,因为他们老是出现在一起,real和estate可以放在一类,dads,guide这种词就看起来有点孤立了,我们就不对他们进行合并了。按这样聚类出现的效果,可以提取文档集合中的近义词,这样当用户检索文档的时候,是用语义级别(近义词集合)去检索了,而不是之前的词的级别。这样一减少我们的检索、存储量,因为这样压缩的文档集合和PCA是异曲同工的,二可以提高我们的用户体验,用户输入一个词,我们可以在这个词的近义词的集合中去找,这是传统的索引无法做到的。
在图上,每一个红色的点,都表示一个词,每一个蓝色的点,都表示一篇文档,这样我们可以对这些词和文档进行聚类,比如说stock 和 market可以放在一类,因为他们老是出现在一起,real和estate可以放在一类,dads,guide这种词就看起来有点孤立了,我们就不对他们进行合并了。按这样聚类出现的效果,可以提取文档集合中的近义词,这样当用户检索文档的时候,是用语义级别(近义词集合)去检索了,而不是之前的词的级别。这样一减少我们的检索、存储量,因为这样压缩的文档集合和PCA是异曲同工的,二可以提高我们的用户体验,用户输入一个词,我们可以在这个词的近义词的集合中去找,这是传统的索引无法做到的。
2.数据分析(data analysis)
我们搜集的数据中总是存在噪声:无论采用的设备多精密,方法有多好,总是会存在一些误差的。如果你们还记得上文提到的,大的奇异值对应了矩阵中的主要信息的话,运用SVD进行数据分析,提取其中的主要部分的话,还是相当合理的。作为例子,假如我们搜集的数据如下所示:
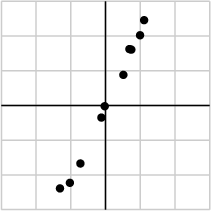
我们将数据用矩阵的形式表示:

经过奇异值分解后,得到
σ1 = 6.04
σ2 = 0.22
由于第一个奇异值远比第二个要大,数据中有包含一些噪声,第二个奇异值在原始矩阵分解相对应的部分可以忽略。经过SVD分解后,保留了主要样本点如图所示
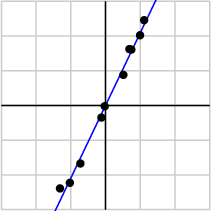
就保留主要样本数据来看,该过程跟PCA( principal component analysis)技术有一些联系,PCA也使用了SVD去检测数据间依赖和冗余信息.。
--------------------------先更到这里,有时间再更-----------------
更多详细信息可以参考《神奇的矩阵》和《神奇的矩阵第二季》,或者加群了解有关线性代数和矩阵的知识。
参考文献
1. We recommend a singular value decomposition
2. Singular value decomposition
4. 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用
5. 本文由LeftNotEasy发布于LeftNotEasy - 博客园,部分修改


 浙公网安备 33010602011771号
浙公网安备 33010602011771号