【ML算法基础】马氏距离

 

 

 

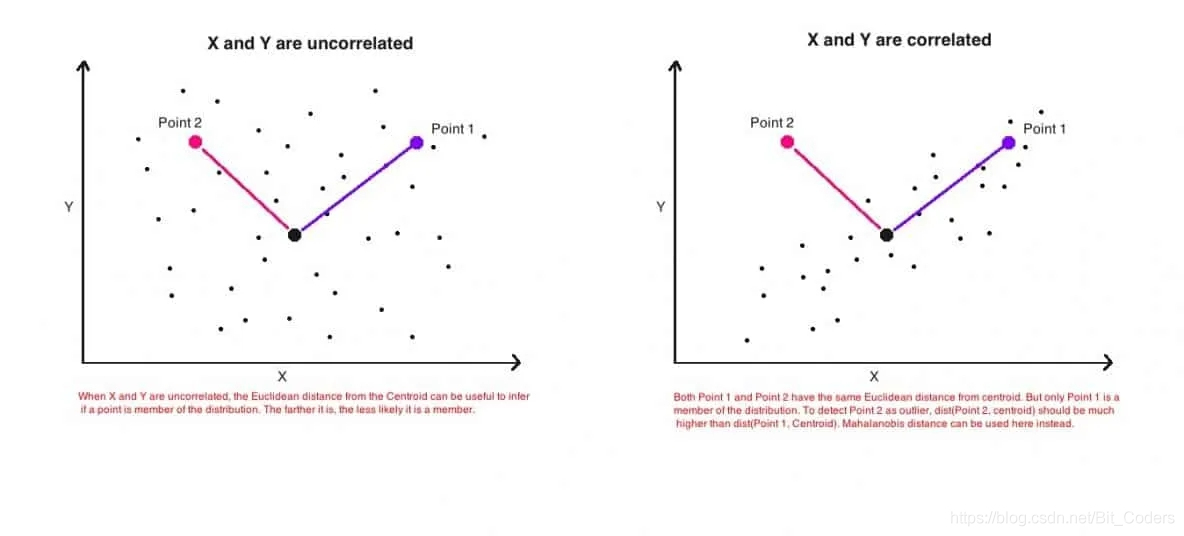
直观解释
( x − μ ) (\bold{x}-\bold{\mu})(x−μ)本质上是向量与平均值的距离。然后，将其除以协方差矩阵（或乘以协方差矩阵的逆数）。

这实际上是多元变量的常规标准化（z =（x – mu）/ sigma）。也就是说，z =（x向量）–（平均向量）/（协方差矩阵）。

如果数据集中的变量高度相关，则协方差将很高。除以较大的协方差将有效缩短距离。

同样，如果X不相关，则协方差也不高，距离也不会减少太多。

因此，它有效地解决了规模问题以及前文中谈到的变量之间的相关性。

 

两个矩形框的相似度：

 

 

参考

1. 马氏距离详解（数学原理、适用场景、应用示例代码）；

完