【ML算法基础】匈牙利算法理解

前言

匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，匈牙利算法（Hungarian Algorithm）与KM算法（Kuhn-Munkres Algorithm）是做多目标跟踪的小伙伴很容易在论文中见到的两种算法。他们都是用来解决多目标跟踪中的数据关联问题。匈牙利算法与KM算法都是为了求解二分图的最大匹配问题，Kuhn–Munkres算法在匈牙利算法的基础上解决加权二分图匹配问题。

矩形矩阵的分配问题；

递归算法，匈牙利算法的 DFS 和 BFS 版本的代码；

使用lap.lapjv实现线性分配（可以作为匈牙利算法的实现），官方文档使用lapjv实现指派问题的算法是Jonker-Volgenant algorithm。这个算法比匈牙利算法快得多。

分配问题的算法：Munkres算法\拍卖算法\lapjv算法\匈牙利算法等。

$O (n^{3})$

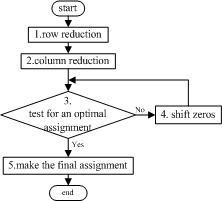
step1）row reduction：每一行减去该行的最小值；
step2）column resuction：每一列减去该列的最小值；
step3）test for an optimal assignment: 使用最少的直线覆盖矩阵中的所有数值零；如果满足最少直线数目，转step5)直接可以得到最终的分配方案；如果不满足则转step4).
step4）shift zeros：如果不满足最少直线数目，需要转移数值零到直线未覆盖的位置，来增加覆盖0的最少直线数目；
step4.1）找出没被直线覆盖的值中的最小值；
step4.2）未被直线覆盖的数值都减去这个最小值，然后在交叉的位置加上这个最小值；
step4.3）把直线移除，回到step3；
step5）making the final assignment：选择最少直线数目个不同行不同列的0即最终方案，可能会有不同的分配方案；

对于非方阵的问题，只需要用0填充缺失的行或列，然后在第五步确定最终分配方案时，把它们移除。

算法时间复杂度计算

第一步和第二步对矩阵中元素进行了扫描和更新。由于矩阵中一共有n^2个元素，则这两步的时间复杂度均为O(n^2)；第三步是用直线覆盖所有零元素，因此该步需要访问所有零元素，其中零元素个数最多达n^2。第四步需要扫描和更新矩阵中的元素，最多n^2个。因此第三步，第四步均为O(n^2)。但是第三，四步需要迭代进行，直到最少直线数等于n时，停止迭代。每一次迭代，最少直线数都会至少增加1条，因此最多迭代次数为n次。因此，第三步，第四步时间复杂度最高为O(n^3)。第五步得到最终分配方案，时间复杂度为O(n)。因此匈牙利算法的时间复杂度为O(n^3)。

流程图

代码实现

matlab_lapjv

% https://www.mathworks.com/matlabcentral/fileexchange/26836-lapjv-jonker-volgenant-algorithm-for-linear-assignment-problem-v3-0
function [rowsol,cost,v,u,costMat] = lapjv(costMat,resolution)
% LAPJV  Jonker-Volgenant Algorithm for Linear Assignment Problem.
%
% [ROWSOL,COST,v,u,rMat] = LAPJV(COSTMAT, resolution) returns the optimal column indices,
% ROWSOL, assigned to row in solution, and the minimum COST based on the
% assignment problem represented by the COSTMAT, where the (i,j)th element
% represents the cost to assign the jth job to the ith worker.
% The second optional input can be used to define data resolution to
% accelerate speed.
% Other output arguments are:
% v: dual variables, column reduction numbers.
% u: dual variables, row reduction numbers.
% rMat: the reduced cost matrix.
%
% For a rectangular (nonsquare) costMat, rowsol is the index vector of the
% larger dimension assigned to the smaller dimension.
%
% [ROWSOL,COST,v,u,rMat] = LAPJV(COSTMAT,resolution) accepts the second
% input argument as the minimum resolution to differentiate costs between
% assignments. The default is eps.
%
% Known problems: The original algorithm was developed for integer costs.
% When it is used for real (floating point) costs, sometime the algorithm
% will take an extreamly long time. In this case, using a reasonable large
% resolution as the second arguments can significantly increase the
% solution speed.
%
% See also munkres, Hungarian
% version 1.0 by Yi Cao at Cranfield University on 3rd March 2010
% version 1.1 by Yi Cao at Cranfield University on 19th July 2010
% version 1.2 by Yi Cao at Cranfield University on 22nd July 2010
% version 2.0 by Yi Cao at Cranfield University on 28th July 2010
% version 2.1 by Yi Cao at Cranfield University on 13th August 2010
% version 2.2 by Yi Cao at Cranfield University on 17th August 2010
% version 3.0 by Yi Cao at Cranfield University on 10th April 2013
% This Matlab version is developed based on the orginal C++ version coded
% by Roy Jonker @ MagicLogic Optimization Inc on 4 September 1996.
% Reference:
% R. Jonker and A. Volgenant, "A shortest augmenting path algorithm for
% dense and spare linear assignment problems", Computing, Vol. 38, pp.
% 325-340, 1987.
%
% Examples
% Example 1: a 5 x 5 example
%{
[rowsol,cost] = lapjv(magic(5));
disp(rowsol); % 3 2 1 5 4
disp(cost);   %15
%}
% Example 2: 1000 x 1000 random data
%{
n=1000;
A=randn(n)./rand(n);
tic
[a,b]=lapjv(A);
toc                 % about 0.5 seconds 
%}
% Example 3: nonsquare test
%{
n=100;
A=1./randn(n);
tic
[a,b]=lapjv(A);
toc % about 0.2 sec
A1=[A zeros(n,1)+max(max(A))];
tic
[a1,b1]=lapjv(A1);
toc % about 0.01 sec. The nonsquare one can be done faster!
%check results
disp(norm(a-a1))
disp(b-b)
%}
if nargin<2
    maxcost=min(1e16,max(max(costMat)));
    resolution=eps(maxcost);
end
% Prepare working data
[rdim,cdim] = size(costMat);
M=min(min(costMat));
if rdim>cdim
    costMat = costMat';
    [rdim,cdim] = size(costMat);
    swapf=true;
else
    swapf=false;
end
dim=cdim;
costMat = [costMat;2*M+zeros(cdim-rdim,cdim)];
costMat(costMat~=costMat)=Inf;
maxcost=max(costMat(costMat<Inf))*dim+1;
if isempty(maxcost)
    maxcost = Inf;
end
costMat(costMat==Inf)=maxcost;
% free = zeros(dim,1);      % list of unssigned rows
% colist = 1:dim;         % list of columns to be scaed in various ways
% d = zeros(1,dim);       % 'cost-distance' in augmenting path calculation.
% pred = zeros(dim,1);    % row-predecessor of column in augumenting/alternating path.
v = zeros(1,dim);         % dual variables, column reduction numbers.
rowsol = zeros(1,dim)-1;  % column assigned to row in solution
colsol = zeros(dim,1)-1;  % row assigned to column in solution
numfree=0;
free = zeros(dim,1);      % list of unssigned rows
matches = zeros(dim,1);   % counts how many times a row could be assigned.
% The Initilization Phase
% column reduction
for j=dim:-1:1 % reverse order gives better results
    % find minimum cost over rows
    [v(j), imin] = min(costMat(:,j));
    if ~matches(imin)
        % init assignement if minimum row assigned for first time
        rowsol(imin)=j;
        colsol(j)=imin;
    elseif v(j)<v(rowsol(imin))
        j1=rowsol(imin);
        rowsol(imin)=j;
        colsol(j)=imin;
        colsol(j1)=-1;
    else
        colsol(j)=-1; % row already assigned, column not assigned.
    end
    matches(imin)=matches(imin)+1;
end
% Reduction transfer from unassigned to assigned rows
for i=1:dim
    if ~matches(i)      % fill list of unaasigned 'free' rows.
        numfree=numfree+1;
        free(numfree)=i;
    else
        if matches(i) == 1 % transfer reduction from rows that are assigned once.
            j1 = rowsol(i);
            x = costMat(i,:)-v;
            x(j1) = maxcost;
            v(j1) = v(j1) - min(x);
        end
    end
end
% Augmenting reduction of unassigned rows
loopcnt = 0;
while loopcnt < 2
    loopcnt = loopcnt + 1;
    % scan all free rows
    % in some cases, a free row may be replaced with another one to be scaed next
    k = 0;
    prvnumfree = numfree;
    numfree = 0;    % start list of rows still free after augmenting row reduction.
    while k < prvnumfree
        k = k+1;
        i = free(k);
        % find minimum and second minimum reduced cost over columns
        x = costMat(i,:) - v;
        [umin, j1] = min(x);
        x(j1) = maxcost;
        [usubmin, j2] = min(x);
        i0 = colsol(j1);
        if usubmin - umin > resolution 
            % change the reduction of the minmum column to increase the
            % minimum reduced cost in the row to the subminimum.
            v(j1) = v(j1) - (usubmin - umin);
        else % minimum and subminimum equal.
            if i0 > 0 % minimum column j1 is assigned.
                % swap columns j1 and j2, as j2 may be unassigned.
                j1 = j2;
                i0 = colsol(j2);
            end
        end
        % reassign i to j1, possibly de-assigning an i0.
        rowsol(i) = j1;
        colsol(j1) = i;
        if i0 > 0 % ,inimum column j1 assigned easier
            if usubmin - umin > resolution
                % put in current k, and go back to that k.
                % continue augmenting path i - j1 with i0.
                free(k)=i0;
                k=k-1;
            else
                % no further augmenting reduction possible
                % store i0 in list of free rows for next phase.
                numfree = numfree + 1;
                free(numfree) = i0;
            end
        end
    end
end
% Augmentation Phase
% augment solution for each free rows
for f=1:numfree
    freerow = free(f); % start row of augmenting path
    % Dijkstra shortest path algorithm.
    % runs until unassigned column added to shortest path tree.
    d = costMat(freerow,:) - v;
    pred = freerow(1,ones(1,dim));
    collist = 1:dim;
    low = 1; % columns in 1...low-1 are ready, now none.
    up = 1; % columns in low...up-1 are to be scaed for current minimum, now none.
    % columns in up+1...dim are to be considered later to find new minimum,
    % at this stage the list simply contains all columns.
    unassignedfound = false;
    while ~unassignedfound
        if up == low    % no more columns to be scaned for current minimum.
            last = low-1;
            % scan columns for up...dim to find all indices for which new minimum occurs. 
            % store these indices between low+1...up (increasing up).
            minh = d(collist(up));
            up = up + 1;
            for k=up:dim
                j = collist(k);
                h = d(j);
                if h<=minh
                    if h<minh
                        up = low;
                        minh = h;
                    end
                    % new index with same minimum, put on index up, and extend list.
                    collist(k) = collist(up);
                    collist(up) = j;
                    up = up +1;
                end
            end
            % check if any of the minimum columns happens to be unassigned.
            % if so, we have an augmenting path right away.
            for k=low:up-1
                if colsol(collist(k)) < 0
                    endofpath = collist(k); 
                    unassignedfound = true;
                    break
                end
            end
        end
        if ~unassignedfound
            % update 'distances' between freerow and all unscanned columns,
            % via next scanned column.
            j1 = collist(low);
            low=low+1;
            i = colsol(j1); %line 215
            x = costMat(i,:)-v;
            h = x(j1) - minh;
            xh = x-h;
            k=up:dim;
            j=collist(k);
            vf0 = xh<d;
            vf = vf0(j);
            vj = j(vf);
            vk = k(vf);
            pred(vj)=i;
            v2 = xh(vj);
            d(vj)=v2;
            vf = v2 == minh; % new column found at same minimum value
            j2 = vj(vf);
            k2 = vk(vf);
            cf = colsol(j2)<0; 
            if any(cf) % unassigned, shortest augmenting path is complete.
                i2 = find(cf,1);                
                endofpath = j2(i2);
                unassignedfound = true;
            else 
                i2 = numel(cf)+1;
            end
            % add to list to be scaned right away
            for k=1:i2-1
                collist(k2(k)) = collist(up);
                collist(up) = j2(k);
                up = up + 1;
            end
        end
    end
    % update column prices
    j1=collist(1:last+1);
    v(j1) = v(j1) + d(j1) - minh;
    % reset row and column assignments along the alternating path
    while 1
        i=pred(endofpath);
        colsol(endofpath)=i;
        j1=endofpath;
        endofpath=rowsol(i);
        rowsol(i)=j1;
        if (i==freerow)
            break
        end
    end
end
rowsol = rowsol(1:rdim);
u=diag(costMat(:,rowsol))-v(rowsol)';
u=u(1:rdim);
v=v(1:cdim);
cost = sum(u)+sum(v(rowsol));
costMat=costMat(1:rdim,1:cdim);
costMat = costMat - u(:,ones(1,cdim)) - v(ones(rdim,1),:);
if swapf
    costMat = costMat';
    t=u';
    u=v';
    v=t;
end
if cost>maxcost
    cost=Inf;
end

matlab_hungarian

%https://web.archive.org/web/20120816044907/http://www.mathworks.com/matlabcentral/fileexchange/11609-hungarian-algorithm/content/Hungarian.m
function [Matching,Cost] = Hungarian(Perf)
% 
% [MATCHING,COST] = Hungarian_New(WEIGHTS)
%
% A function for finding a minimum edge weight matching given a MxN Edge
% weight matrix WEIGHTS using the Hungarian Algorithm.
%
% An edge weight of Inf indicates that the pair of vertices given by its
% position have no adjacent edge.
%
% MATCHING return a MxN matrix with ones in the place of the matchings and
% zeros elsewhere.
% 
% COST returns the cost of the minimum matching

% Written by: Alex Melin 30 June 2006


 % Initialize Variables
 Matching = zeros(size(Perf));

% Condense the Performance Matrix by removing any unconnected vertices to
% increase the speed of the algorithm

  % Find the number in each column that are connected
    num_y = sum(~isinf(Perf),1);
  % Find the number in each row that are connected
    num_x = sum(~isinf(Perf),2);
    
  % Find the columns(vertices) and rows(vertices) that are isolated
    x_con = find(num_x~=0);
    y_con = find(num_y~=0);
    
  % Assemble Condensed Performance Matrix
    P_size = max(length(x_con),length(y_con));
    P_cond = zeros(P_size);
    P_cond(1:length(x_con),1:length(y_con)) = Perf(x_con,y_con);
    if isempty(P_cond)
      Cost = 0;
      return
    end

    % Ensure that a perfect matching exists
      % Calculate a form of the Edge Matrix
      Edge = P_cond;
      Edge(P_cond~=Inf) = 0;
      % Find the deficiency(CNUM) in the Edge Matrix
      cnum = min_line_cover(Edge);
    
      % Project additional vertices and edges so that a perfect matching
      % exists
      Pmax = max(max(P_cond(P_cond~=Inf)));
      P_size = length(P_cond)+cnum;
      P_cond = ones(P_size)*Pmax;
      P_cond(1:length(x_con),1:length(y_con)) = Perf(x_con,y_con);
   
%*************************************************
% MAIN PROGRAM: CONTROLS WHICH STEP IS EXECUTED
%*************************************************
  exit_flag = 1;
  stepnum = 1;
  while exit_flag
    switch stepnum
      case 1
        [P_cond,stepnum] = step1(P_cond);
      case 2
        [r_cov,c_cov,M,stepnum] = step2(P_cond);
      case 3
        [c_cov,stepnum] = step3(M,P_size);
      case 4
        [M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(P_cond,r_cov,c_cov,M);
      case 5
        [M,r_cov,c_cov,stepnum] = step5(M,Z_r,Z_c,r_cov,c_cov);
      case 6
        [P_cond,stepnum] = step6(P_cond,r_cov,c_cov);
      case 7
        exit_flag = 0;
    end
  end

% Remove all the virtual satellites and targets and uncondense the
% Matching to the size of the original performance matrix.
Matching(x_con,y_con) = M(1:length(x_con),1:length(y_con));
Cost = sum(sum(Perf(Matching==1)));

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%   STEP 1: Find the smallest number of zeros in each row
%           and subtract that minimum from its row
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [P_cond,stepnum] = step1(P_cond)

  P_size = length(P_cond);
  
  % Loop throught each row
  for ii = 1:P_size
    rmin = min(P_cond(ii,:));
    P_cond(ii,:) = P_cond(ii,:)-rmin;
  end

  stepnum = 2;
  
%**************************************************************************  
%   STEP 2: Find a zero in P_cond. If there are no starred zeros in its
%           column or row start the zero. Repeat for each zero
%**************************************************************************

function [r_cov,c_cov,M,stepnum] = step2(P_cond)

% Define variables
  P_size = length(P_cond);
  r_cov = zeros(P_size,1);  % A vector that shows if a row is covered
  c_cov = zeros(P_size,1);  % A vector that shows if a column is covered
  M = zeros(P_size);        % A mask that shows if a position is starred or primed
  
  for ii = 1:P_size
    for jj = 1:P_size
      if P_cond(ii,jj) == 0 && r_cov(ii) == 0 && c_cov(jj) == 0
        M(ii,jj) = 1;
        r_cov(ii) = 1;
        c_cov(jj) = 1;
      end
    end
  end
  
% Re-initialize the cover vectors
  r_cov = zeros(P_size,1);  % A vector that shows if a row is covered
  c_cov = zeros(P_size,1);  % A vector that shows if a column is covered
  stepnum = 3;
  
%**************************************************************************
%   STEP 3: Cover each column with a starred zero. If all the columns are
%           covered then the matching is maximum
%**************************************************************************

function [c_cov,stepnum] = step3(M,P_size)

  c_cov = sum(M,1);
  if sum(c_cov) == P_size
    stepnum = 7;
  else
    stepnum = 4;
  end
  
%**************************************************************************
%   STEP 4: Find a noncovered zero and prime it.  If there is no starred
%           zero in the row containing this primed zero, Go to Step 5.  
%           Otherwise, cover this row and uncover the column containing 
%           the starred zero. Continue in this manner until there are no 
%           uncovered zeros left. Save the smallest uncovered value and 
%           Go to Step 6.
%**************************************************************************
function [M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(P_cond,r_cov,c_cov,M)

P_size = length(P_cond);

zflag = 1;
while zflag  
    % Find the first uncovered zero
      row = 0; col = 0; exit_flag = 1;
      ii = 1; jj = 1;
      while exit_flag
          if P_cond(ii,jj) == 0 && r_cov(ii) == 0 && c_cov(jj) == 0
            row = ii;
            col = jj;
            exit_flag = 0;
          end      
          jj = jj + 1;      
          if jj > P_size; jj = 1; ii = ii+1; end      
          if ii > P_size; exit_flag = 0; end      
      end

    % If there are no uncovered zeros go to step 6
      if row == 0
        stepnum = 6;
        zflag = 0;
        Z_r = 0;
        Z_c = 0;
      else
        % Prime the uncovered zero
        M(row,col) = 2;
        % If there is a starred zero in that row
        % Cover the row and uncover the column containing the zero
          if sum(find(M(row,:)==1)) ~= 0
            r_cov(row) = 1;
            zcol = find(M(row,:)==1);
            c_cov(zcol) = 0;
          else
            stepnum = 5;
            zflag = 0;
            Z_r = row;
            Z_c = col;
          end            
      end
end
  
%**************************************************************************
% STEP 5: Construct a series of alternating primed and starred zeros as
%         follows.  Let Z0 represent the uncovered primed zero found in Step 4.
%         Let Z1 denote the starred zero in the column of Z0 (if any). 
%         Let Z2 denote the primed zero in the row of Z1 (there will always
%         be one).  Continue until the series terminates at a primed zero
%         that has no starred zero in its column.  Unstar each starred 
%         zero of the series, star each primed zero of the series, erase 
%         all primes and uncover every line in the matrix.  Return to Step 3.
%**************************************************************************

function [M,r_cov,c_cov,stepnum] = step5(M,Z_r,Z_c,r_cov,c_cov)

  zflag = 1;
  ii = 1;
  while zflag 
    % Find the index number of the starred zero in the column
    rindex = find(M(:,Z_c(ii))==1);
    if rindex > 0
      % Save the starred zero
      ii = ii+1;
      % Save the row of the starred zero
      Z_r(ii,1) = rindex;
      % The column of the starred zero is the same as the column of the 
      % primed zero
      Z_c(ii,1) = Z_c(ii-1);
    else
      zflag = 0;
    end
    
    % Continue if there is a starred zero in the column of the primed zero
    if zflag == 1;
      % Find the column of the primed zero in the last starred zeros row
      cindex = find(M(Z_r(ii),:)==2);
      ii = ii+1;
      Z_r(ii,1) = Z_r(ii-1);
      Z_c(ii,1) = cindex;    
    end    
  end
  
  % UNSTAR all the starred zeros in the path and STAR all primed zeros
  for ii = 1:length(Z_r)
    if M(Z_r(ii),Z_c(ii)) == 1
      M(Z_r(ii),Z_c(ii)) = 0;
    else
      M(Z_r(ii),Z_c(ii)) = 1;
    end
  end
  
  % Clear the covers
  r_cov = r_cov.*0;
  c_cov = c_cov.*0;
  
  % Remove all the primes
  M(M==2) = 0;

stepnum = 3;

% *************************************************************************
% STEP 6: Add the minimum uncovered value to every element of each covered
%         row, and subtract it from every element of each uncovered column.  
%         Return to Step 4 without altering any stars, primes, or covered lines.
%**************************************************************************

function [P_cond,stepnum] = step6(P_cond,r_cov,c_cov)
a = find(r_cov == 0);
b = find(c_cov == 0);
minval = min(min(P_cond(a,b)));

P_cond(find(r_cov == 1),:) = P_cond(find(r_cov == 1),:) + minval;
P_cond(:,find(c_cov == 0)) = P_cond(:,find(c_cov == 0)) - minval;

stepnum = 4;

function cnum = min_line_cover(Edge)

  % Step 2
    [r_cov,c_cov,M,stepnum] = step2(Edge);
  % Step 3
    [c_cov,stepnum] = step3(M,length(Edge));
  % Step 4
    [M,r_cov,c_cov,Z_r,Z_c,stepnum] = step4(Edge,r_cov,c_cov,M);
  % Calculate the deficiency
    cnum = length(Edge)-sum(r_cov)-sum(c_cov);

matlab_Munkres　

function [assignment,cost] = munkres(costMat)
% MUNKRES   Munkres Assign Algorithm 
%
% [ASSIGN,COST] = munkres(COSTMAT) returns the optimal assignment in ASSIGN
% with the minimum COST based on the assignment problem represented by the
% COSTMAT, where the (i,j)th element represents the cost to assign the jth
% job to the ith worker.
%
% This is vectorized implementation of the algorithm. It is the fastest
% among all Matlab implementations of the algorithm.
% Examples
% Example 1: a 5 x 5 example
%{
[assignment,cost] = munkres(magic(5));
[assignedrows,dum]=find(assignment);
disp(assignedrows'); % 3 2 1 5 4
disp(cost); %15
%}
% Example 2: 400 x 400 random data
%{
n=400;
A=rand(n);
tic
[a,b]=munkres(A);
toc                 % about 6 seconds 
%}
% Reference:
% "Munkres' Assignment Algorithm, Modified for Rectangular Matrices", 
% http://csclab.murraystate.edu/bob.pilgrim/445/munkres.html
% version 1.0 by Yi Cao at Cranfield University on 17th June 2008
assignment = false(size(costMat));
cost = 0;
costMat(costMat~=costMat)=Inf;
validMat = costMat<Inf;
validCol = any(validMat);
validRow = any(validMat,2);
nRows = sum(validRow);
nCols = sum(validCol);
n = max(nRows,nCols);
if ~n
    return
end
    
dMat = zeros(n);
dMat(1:nRows,1:nCols) = costMat(validRow,validCol);
%*************************************************
% Munkres' Assignment Algorithm starts here
%*************************************************
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%   STEP 1: Subtract the row minimum from each row.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 dMat = bsxfun(@minus, dMat, min(dMat,[],2));
%**************************************************************************  
%   STEP 2: Find a zero of dMat. If there are no starred zeros in its
%           column or row start the zero. Repeat for each zero
%**************************************************************************
zP = ~dMat;
starZ = false(n);
while any(zP(:))
    [r,c]=find(zP,1);
    starZ(r,c)=true;
    zP(r,:)=false;
    zP(:,c)=false;
end
while 1
%**************************************************************************
%   STEP 3: Cover each column with a starred zero. If all the columns are
%           covered then the matching is maximum
%**************************************************************************
    primeZ = false(n);
    coverColumn = any(starZ);
    if ~any(~coverColumn)
        break
    end
    coverRow = false(n,1);
    while 1
        %**************************************************************************
        %   STEP 4: Find a noncovered zero and prime it.  If there is no starred
        %           zero in the row containing this primed zero, Go to Step 5.  
        %           Otherwise, cover this row and uncover the column containing 
        %           the starred zero. Continue in this manner until there are no 
        %           uncovered zeros left. Save the smallest uncovered value and 
        %           Go to Step 6.
        %**************************************************************************
        zP(:) = false;
        zP(~coverRow,~coverColumn) = ~dMat(~coverRow,~coverColumn);
        Step = 6;
        while any(any(zP(~coverRow,~coverColumn)))
            [uZr,uZc] = find(zP,1);
            primeZ(uZr,uZc) = true;
            stz = starZ(uZr,:);
            if ~any(stz)
                Step = 5;
                break;
            end
            coverRow(uZr) = true;
            coverColumn(stz) = false;
            zP(uZr,:) = false;
            zP(~coverRow,stz) = ~dMat(~coverRow,stz);
        end
        if Step == 6
            % *************************************************************************
            % STEP 6: Add the minimum uncovered value to every element of each covered
            %         row, and subtract it from every element of each uncovered column.
            %         Return to Step 4 without altering any stars, primes, or covered lines.
            %**************************************************************************
            M=dMat(~coverRow,~coverColumn);
            minval=min(min(M));
            if minval==inf
                return
            end
            dMat(coverRow,coverColumn)=dMat(coverRow,coverColumn)+minval;
            dMat(~coverRow,~coverColumn)=M-minval;
        else
            break
        end
    end
    %**************************************************************************
    % STEP 5:
    %  Construct a series of alternating primed and starred zeros as
    %  follows:
    %  Let Z0 represent the uncovered primed zero found in Step 4.
    %  Let Z1 denote the starred zero in the column of Z0 (if any).
    %  Let Z2 denote the primed zero in the row of Z1 (there will always
    %  be one).  Continue until the series terminates at a primed zero
    %  that has no starred zero in its column.  Unstar each starred
    %  zero of the series, star each primed zero of the series, erase
    %  all primes and uncover every line in the matrix.  Return to Step 3.
    %**************************************************************************
    rowZ1 = starZ(:,uZc);
    starZ(uZr,uZc)=true;
    while any(rowZ1)
        starZ(rowZ1,uZc)=false;
        uZc = primeZ(rowZ1,:);
        uZr = rowZ1;
        rowZ1 = starZ(:,uZc);
        starZ(uZr,uZc)=true;
    end
end
% Cost of assignment
assignment(validRow,validCol) = starZ(1:nRows,1:nCols);
cost = sum(costMat(assignment));

参考

1. 目标跟踪初探（DeepSORT）；

2. 趣写算法系列之--匈牙利算法；

3. 带你入门多目标跟踪（三）匈牙利算法&KM算法；

4. matlab_Hungarian;

5. 匈牙利演算法 (Hungarian Algorithm );

6. 演算法學習筆記：匈牙利演算法;

7. KM算法原理+证明；

8. LAPJV_algorithm_c;

9. 使用lap.lapjv实现匈牙利算法的线性分配；

10. matlab_lapjv；

11. Munkres Assignment Algorithm;