并查集

并查集

如果有一个关系网，我们需要建立两点之间的关系，如果仅用一维链表 ，则有可能无法考虑到两点同为一点 “儿子”的 情况，则 我们需要建立一个方式，从而直接对比两点“祖父”。

一 .递归查询

int find(int x){
　　if(fa[x]==x)return x;//只有祖父自环，如果他也自环，则找到父节点
　　return find(fa[x]);//不然往父节点继续靠近
}

 

二.合并两节点

void add(int xx,int yy){
　　int fa_xx=find(xx);
　　int fa_yy=find(yy);
　　fa[fa_xx]=fa_yy;//将两者合并
}

 

以上为基础并查集，记得要初始化：在每一个数在建立关系前与自己自环.

现在我们可以开始想想大样例该如何过了。

加如题目告诉你 1-7，7-3，3-4，5-6，2-6，1-2，然后询问你5，4是否有关系，按原本方法可得画图：

 

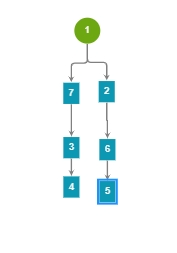
 根据树形图可知；两者都是1的子孙，但是查询次数多，如果更大的数据可能会爆，所以我们可以考虑在每一次更新后将点值更新为祖先值。

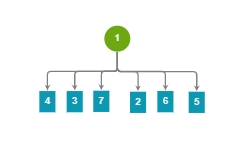
 如此反复跟新，便可以将速度大为优化，代码中优化也很简单 

int find(int x){
　　if(fa[x]==x)return x;//只有祖父自环，如果他也自环，则找到父节点

　　fa[x]=find(fa[x]);//每次更新点值
　　return fa[x];//不然往父节点继续靠近
}

如此这般 便完成优化了。

三.例题试炼

1.P1551 亲戚 

简单模板，直接调用即可

#include<bits/stdc++.h>
using namespace std;
int n,m,p,t[100000]; int a,b;
int find(int x){
    if(t[x]==x)return x;
    return t[x]=find(t[x]);
}
void add(int x,int y){
    int fa_x=find(x);
    int fa_y=find(y);
    t[fa_x]=fa_y;
}
int main(){
    
    cin>>n>>m>>p;
    for(int i=1;i<=n;i++)t[i]=i;
    for(int i=1;i<=m;i++){
        cin>>a>>b;
        add(a,b);
    }
    for(int i=1;i<=p;i++){
        cin>>a>>b;
        if(find(a)==find(b))cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    
    return 0;
}

2.P3367 【模板】并查集

#include<bits/stdc++.h>
using namespace std;
int n,m,z,x,y;
int a[10010];
int find(int q){
    if(a[q]==q)return q;
    return a[q]=find(a[q]);
}
int main(){    
    cin>>n>>m;
    for(int i=1;i<=n;i++)a[i]=i;
    for(int i=1;i<=m;i++){
        cin>>z>>x>>y;
        if(z==1){
            a[find(x)]=find(y);
            
        }else{
            if(find(x)==find(y))cout<<"Y"<<endl;
            else cout<<"N"<<endl;
        }
    }
     

return 0;
}

 3.水绿P3420 [POI2005] SKA-Piggy Banks

本题就是并查集的一个变式，每次查看是否自环，如果自环就统计，反之则将钥匙箱号码赋给并查集数组

#include<bits/stdc++.h>
using namespace std;
int n,m,fa[1000005],a[1000005],total;
int find(int x){
    if(fa[x]==x)return x;
    else return fa[x]=find(fa[x]);
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        if(find(a[i])==i)total++;//判断是否自环
        else fa[i]=a[i];//重新赋值
    }
    cout<<total;
return 0;
}