图论

注：本文内可能有不属于主题内部的算法，因为是一起学的，所以就顺带讲上了。

一，堆

因为堆是一棵完全二叉树，所以对于一个节点数为n的堆，它的高度不会超过log2n

所以对于插入，删除操作复杂度为O(log2n)

查询堆顶操作的复杂度为O(1)

链接材料：堆简介

　　　　　二叉堆

推荐博文：浅析基础数据结构-二叉堆 - henry_y - 博客园

总结要点：利用二叉树维护一个最大/小值（通过不断移动父/子节点获得）；

算法笔记-堆

堆（

堆中某个结点的值总是不大于或不小于其父结点的值；

堆总是一棵完全二叉树。

上面提到的性质

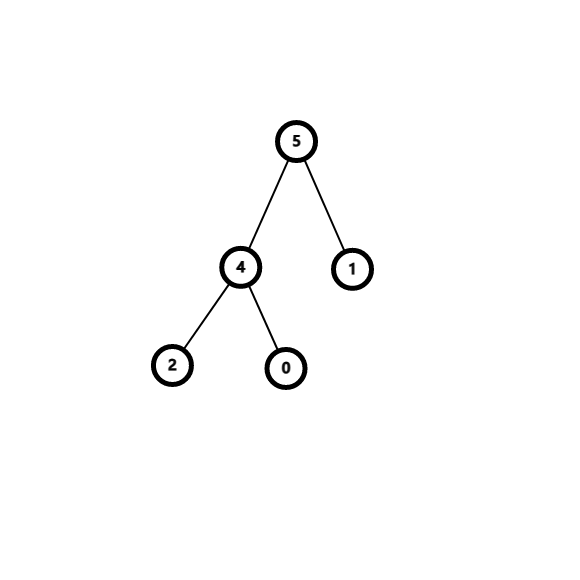
如上是大根堆。

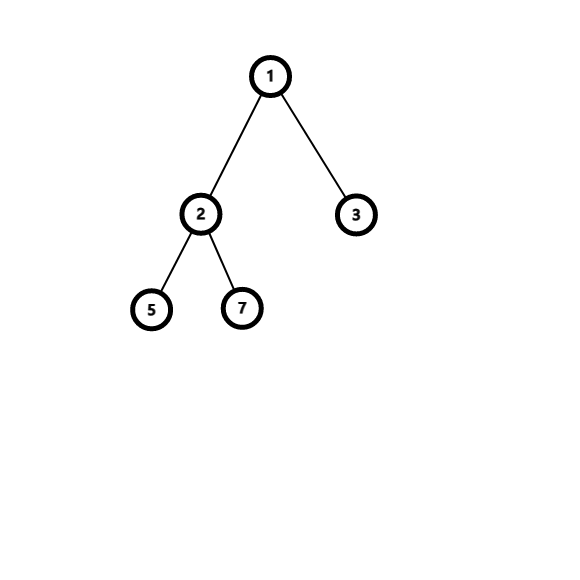
如上是小根堆。

　　　　　　　　　　----上述内容摘录自算法笔记-堆 - __er's Blog - 洛谷博客 (luogu.com.cn)

此二叉树性质为父节点为n,即左子节点为2*n,右子节点为2*n+1;

操作过程（添加）：此图为大根树

二叉堆的插入操作

临时补充（后面会用到）：

条件运算符

条件运算符可以看作 if 语句的简写，a ? b : c 中如果表达式 a 成立，那么这个条件表达式的结果是 b，否则条件表达式的结果是 c。

重点来临！！！：

插入操作

插入操作是指向二叉堆中插入一个元素，要保证插入后也是一棵完全二叉树。

最简单的方法就是，最下一层最右边的叶子之后插入。

如果最下一层已满，就新增一层。

插入之后可能会不满足堆性质？

向上调整：如果这个结点的权值大于它父亲的权值，就交换，重复此过程直到不满足或者到根。

可以证明，插入之后向上调整后，没有其他结点会不满足堆性质。

向上调整的时间复杂度是 O(log n) $O(\log n)$ 的。

因为

push 函数为 (注意此处l(x)和r(x)的创建中都多加了1)：

 1 void push(int x) {
 2     int pos = siz++;//在堆底插入
 3     /*上调操作*/while (pos > 0) {
 4         if (heap[f(pos)] <= x) {//如果父结点小于当前结点，满足性质
 5             break;//停止
 6         }
 7         heap[pos] = heap[f(pos)], pos = f(pos);//互换位置
 8     }
 9     heap[pos] = x;//确定位置后赋值
10     return;
11 }

删除操作

删除操作指删除堆中最大的元素，即删除根结点。

但是如果直接删除，则变成了两个堆，难以处理。

所以不妨考虑插入操作的逆过程，设法将根结点移到最后一个结点，然后直接删掉。

然而实际上不好做，我们通常采用的方法是，把根结点和最后一个结点直接交换。

于是直接删掉（在最后一个结点处的）根结点，但是新的根结点可能不满足堆性质……

向下调整：在该结点的儿子中，找一个最大的，与该结点交换，重复此过程直到底层。

可以证明，删除并向下调整后，没有其他结点不满足堆性质。

时间复杂度 O(log n) $O(\log n)$ 。

增加某个点的权值

很显然，直接修改后，向上调整一次即可，时间复杂度为O(log n) $O(\log n)$ 。

因为

pop 函数为 (注意此处l(x)和r(x)的创建中都多加了1)：

 1 void pop() {
 2     int pos = 0, x = heap[--siz];
 3     while (l(pos) < siz) {
 4         int t = (heap[l(pos)] < heap[r(pos)]) ? l(pos) : r(pos);//找较小儿子
 5         /*下调操作*/if (heap[t] >= x) {
 6             break;
 7         }
 8         heap[pos] = heap[t], pos = t;
 9     }
10 
11     heap[pos] = x;//同上
12     return;
13 }

注：本章内容多有借鉴算法笔记-堆 - __er's Blog - 洛谷博客 (luogu.com.cn)，和二叉堆 - OI Wiki (oi-wiki.org)。

以上为手打堆，接下来介绍一个及其便利的函数，优先队列！

优先队列（STL）

在c++数据库中，要么用 include<queue> 要么用万能头。

调用----1.大根堆 priority_queue<int> q;

　　　 2.小根堆 priority_queue<int,vector<int>,greater<int> > q;

模板例题：P3378 【模板】堆 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

所以可知，调用STL即可。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 priority_queue<int,vector<int>,greater<int> > q;
 4 int n,op,s;
 5 int main(){
 6     ios::sync_with_stdio(false);
 7     cin>>n;
 8     for(int i=1;i<=n;i++){
 9         cin>>op;
10         if(op==1){
11             cin>>s;
12             q.push(s);
13         }
14         if(op==2){
15             cout<<q.top()<<"\n";
16         }
17         if(op==3){
18             q.pop();
19         }
20     }
21     return 0;
22 }

优先队列补充知识：

1.删除其他元素

不过有个小问题就是STL只支持删除堆顶，而不支持删除其他元素

但是问题不大，开一个数组del，在要删除其他元素的时候直接就标记一下del[i]=1，这里的下标是元素的值，然后在查询的时候碰到这个元素被标记了直接弹出然后继续查询就可以了

2.重载运算符

把一种运算符变成另外一种运算符（注意，都必须是原有的运算符），比如把<号重载成>号，这个东西学过STL中的sort的同学应该会比较熟悉

这个在优先队列中有什么用处呢？

之前我们就讲到了，大根堆，小根堆的“大”和“小”都不是传统意义下的“大”和“小”，重载运算符在STL的优先队列中就是用来解决这种“非传统意义的‘大’和‘小’”的

现在你有一个数列，它有权值和优先级两种属性，权值即该数的大小，优先级是给定的，现在要你按照优先级的大小从小到大输出这个数列

~~这不是Treap吗？这不是sort吗？~~

以上两个东西都可以用来实现这道题（逃，而且就实用性而言，sort用来解决这道题是最方便的，但是我们现在要讲的做法是使用堆排序的方式来解决这道题（堆排序是什么？下文堆的应用中有提到）

首先应该想得到结构体，我们定义一个结构体

struct node{
	int val,rnd;
}a[100];

但是使用传统做法是行不通的，在小根堆中是通过比较数的大小来确定各个元素在堆中的位置的，但是对于这个a数组，你是要对比权值val的值，还是要对比优先级rnd的值？

这时候重载运算符就派上用场了

我们在结构体里面再加3行东西

struct node{
	int val,rnd;
    bool operator < (const node&x) const {
		return rnd<x.rnd;
	}
}a[100];

这个玩意为什么要这么写呢？

首先这个玩意是bool类型的，因为你只需要判断这两个是大，还是小；然后，要重载运算符就必须加一个operator这个玩意，不然计算机怎么知道你要干嘛？后面接一个你要重载的运算符，这里是“<”，再后面的括号里面的东西则是你要比较的数据类型，这里是数据类型为node，并且加了一个指针&，将对这个x的修改同步到你实际上要修改的数据那里。然后就是记得加那两个const

然后两个大括号里面就是你重载的内容了，这里是把比较数的大小的小于号，重载成比较node这个数据类型里面的优先级的大小

这个玩意讲的比较多，主要是因为是一个很难懂的东西~~（对我来说？反正当时学的时候就是感觉很晦涩难懂，这里就尽量写详细一点，给和当初的我一样的萌新看一下）~~

而且在实际中，这个东西的用处也很大，就说在堆里面的应用，在NOIP提高，省选的那个级别，就绝对不可能考裸的堆的，往往你要比较的东西就不是数的大小了，而是按照题目要求灵活更改，这时候重载运算符就帮得上很大忙了

这也就是为什么我在前面反复强调，堆里面的大小，并非传统意义下的大小

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　---摘录自浅析基础数据结构-二叉堆 - henry_y - 博客 (cnblogs.com)

二.最短路问题

链接材料：最短路 - OI Wiki (oi-wiki.org)

　　　　　图论相关概念 - OI Wiki (oi-wiki.org)

阅读图论基础概念，然后让我们直接进入算法！

重点来临。。。

1.Dijkstra 算法

以例题学习是个很不错的方法~~P4779 【模板】单源最短路径（标准版） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

以样例为例:

输出 0 2 4 3

解读样例：第一行表示共4个点，6条边，从1开始便利；

接下来为6行每行三个数 a,b,c 分别表示a到b 的边的边权为c ;

如图示：

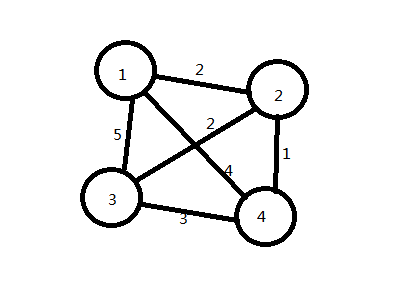
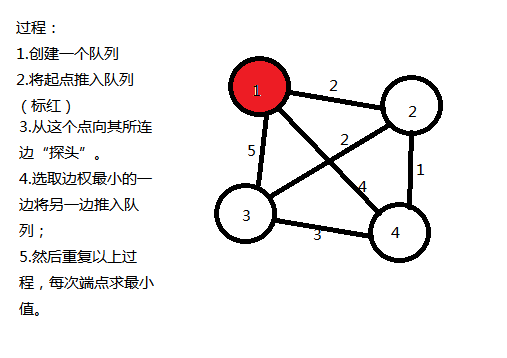
算法过程：

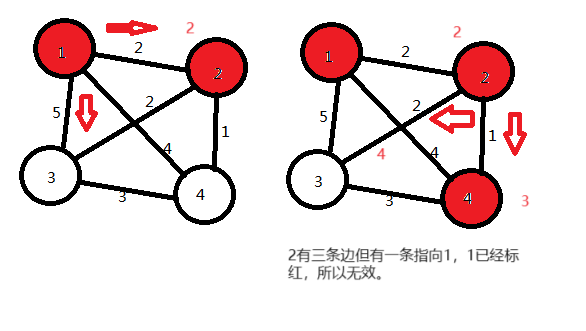
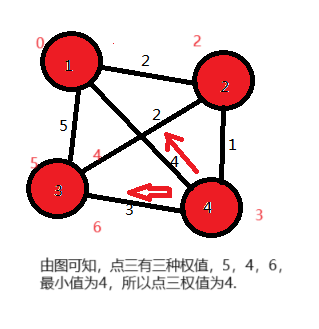
综上，可得结果，0，2，3，4；

接下来，需要我们用代码模拟出这个过程：

首先，这个可以看成一个广搜，每次推进去可以选择的路线，再一一排除；

第二，我们还需要一个工具----链式前向星，用来构建这个图；

链式前向星知识点

逐步分析：

1.输入1 2，代表1连向2。

cnt++;//作为结构体下标，没有意义
head[1]=cnt;//结点1的第一个儿子存在了edge[cnt]里面
edge[cnt].to=2;结点1的儿子是2

2.输入1 3，代表1连向3。

cnt++;
head[1]=cnt;
edge[cnt].to=3;结点1的儿子是3
//这时,3成为了结点1的儿子，不过2被挤了下去...
//所以要引入结构体中next元素，记录：3还有个兄弟（next）是2
//所以代码要换成：
cnt++;
edge[cnt].to=3;//结点1连向3
edge[cnt].next=head[1];//3的兄弟是2
head[1]=cnt;//更新head

由此可得普遍规律：

#include<iostream>

using namespace std;
struct edge 
{ 
    int next;
    int to;
    int wei;
}edge[MAXM];
int head[MAXN];//head[i]为i点的第一条边
int cnt=0;
void addedge(int u,int v,int w) //起点，终点，权值 
{
    edge[++cnt].next=head[u];//更新cnt
    edge[cnt].to=v;
    edge[cnt].w=w;
    head[u]=cnt;
}
int main()
{
    int n;
    for(int i=1;i<=n;i++)
    {
        int a,b,wei;
        addedge(a,b,wei);
        //如果是无向图，还要addedge(b,a,wei);
    }
}

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　----------上述代码部分摘自题解

然后我们就可以得出代码：

 1 #include<bits/stdc++.h>
 2 #define maxn 500010
 3 #define maxx 100010
 4 using namespace std;
 5 int n,m,s; 
 6 int head[maxx],dij[maxx],cnt;//cnt为指针 （位置） ，head 数组存起点 
 7 bool vis[maxx];
 8 struct edge{
 9     int to;//到哪个点 
10     int dis;//边权为几 
11     int next;//起点 
12 }e[maxn];
13 struct priority//重载运算符 （优先队列） 
14 {
15     int ans;
16     int id;
17     bool operator <(const priority &x)const
18     {
19         return x.ans<ans;
20     }
21 };
22 void add_edge(int u,int v,int d){//链式前向星 
23     cnt++;
24     e[cnt].dis =d;
25     e[cnt].next =head[u];
26     e[cnt].to =v;
27     head[u]=cnt;
28 }
29 priority_queue<priority> q;
30 void dijkstra(){
31     int u;
32     q.push((priority){0,s});
33     while(!q.empty()){
34         priority temp=q.top();
35         q.pop();
36         u=temp.id;
37         if(!vis[u]){
38             vis[u]=1;
39             for(int i=head[u];i;i=e[i].next){
40                 int v=e[i].to ;
41                 if(dij[v]>dij[u]+e[i].dis ){
42                     dij[v]=dij[u]+e[i].dis ;
43                     if(!vis[v])q.push((priority){dij[v],v});
44                 }
45             }
46         }
47     }
48     return ;
49 }
50 int main(){
51     cin>>n>>m>>s;
52     for(int i=1;i<=n;i++)dij[i]=2147483647;
53     dij[s]=0;//容易忘记！！！！！！ 
54     for(int i=1;i<=m;i++){//最后一个点不需要再次连边所以是<m
55         int u,v,d;
56         cin>>u>>v>>d;
57         add_edge(u,v,d); //构建图 
58     }
59     dijkstra();
60     for(int i=1;i<=n;i++){
61         cout<<dij[i]<<" ";
62     }
63 return 0;
64 }

圆满结束！

2.Floyd算法

未完待续....

posted @ 2023-10-04 11:31 晓屿阅读(20) 评论(0) 收藏举报

刷新页面返回顶部

小屿的岛