二叉树

一 . 一维数组二叉

所用知识点：1 . 左子树 = 二倍根 ； 2 . 右子树 = 二倍根子树 + 1 ；

　　　　　　2 . 一棵树有 2 的 k 次方 减一个节点 ；

　　　　　　3 . 一棵树最后一行有 2 的 k-1 次方个节点；

解题链接：P4715 【深基16.例1】淘汰赛 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include<bits/stdc++.h>
using namespace std;
int n;
struct human{
    int id,eng;
}a[100000];
int main(){
    cin>>n;
    int f=pow(2,n);//1<<n
    for(int i=1;i<=f;i++){
        cin>>a[f+i-1].eng;
        a[f+i-1].id=i;
    //    cout<<a[f+i-1].id <<" "<<a[f+i-1].eng <<endl;
    }
    for(int j=1;j<=n;j++){
        int o=1;
        for(int i=f+o-1;i<=f+f-1;i+=2){
            if(a[i].eng >a[i+1].eng ){//将获胜方存入位置
                a[i/2].eng =a[i].eng ;
                a[i/2].id =a[i].id ;
            }else{
                a[i/2].eng =a[i+1].eng ;
                a[i/2].id =a[i+1].id ;
            }
            //a[i/2].eng=max(a[i].eng ,a[i+1].eng );
            o+=2;
        }
        f/=2;
    }
    int p=0;
    if(a[2].eng >a[3].eng )cout<<a[3].id;
    else cout<<a[2].id;
return 0;
}

二 . 二叉树的遍历

知识点：1 . 中序遍历：按照左子树，根，右子树的顺序访问节点；

　　　　2 . 前序遍历：按照根，左子树，右子树的顺序访问节点；

　　　　3 . 后序遍历：按照左子树，右子树，根的顺序访问节点。

如此这般，我们可知前序与中序求后序，或根据中序与后序求前序；

【模板】遍历三项

#include<bits/stdc++.h>
using namespace std;
int n;
struct tree{
    int left,right;
}a[10000];
void front(int m){
    if(m==0)return ;
    cout<<m<<" ";//根
    front(a[m].left);//左
    front(a[m].right);//右
}
void mid(int m){
    if(m==0)return ;
    mid(a[m].left);//左
    cout<<m<<" ";//根
    mid(a[m].right);//右
}
void last(int m){
    if(m==0)return ;
    last(a[m].left);//左
    last(a[m].right);//右
    cout<<m<<" ";//根
}
int main(){
    cin>>n; 
    for(int i=1;i<=n;i++){
        cin>>a[i].left>>a[i].right;
    }
    front(1);
    cout<<endl;
    mid(1);
    cout<<endl;
    last(1);
return 0;
}

 

综上，可得例题：P1827 [USACO3.4] 美国血统 American Heritage - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include<bits/stdc++.h>
using namespace std;
string zx,qx,hx,op,i,o;
void bl(string q,string z){
    if(q.empty()) return ;
    char t=q[0];
    int k=z.find(t);//找出地址
    q.erase(q.begin());//用完即丢！方便后续操作 。。。
    bl(q.substr(0,k),z.substr(0,k));
    bl(q.substr(k),z.substr(k+1));//分别便利左儿子和右儿子
    cout<<t;
}

int main(){
    cin>>zx>>qx;
    bl(qx,zx);
    return 0;
}

 【变式】求线序数列：P1030 [NOIP2001 普及组] 求先序排列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include<bits/stdc++.h>
using namespace std;
string q,z,h; 
void dfs_q(string zx,string hx){
    if(zx.empty())return ;
    char s=hx[hx.size()-1];
    cout<<s;
    int pos=zx.find(s,0); 
    string zx_left=zx.substr(0,pos),hx_left=hx.substr(0,pos);//在函数substr内，pos是指下标下一位； 
    string zx_right=zx.substr(pos+1,zx.size()-1),hx_right=hx.substr(hx_left.size(),zx_right.size());
//    cout<<zx_left<<" "<<zx_right<<endl;
//    cout<<hx_left<<" "<<hx_right<<endl;
//    cout<<endl;
    dfs_q(zx_left,hx_left);
    dfs_q(zx_right,hx_right); 
}
int main(){
    cin>>z>>h;
    dfs_q(z,h);
return 0;
}

 

一道很不错的暴力二叉树（广搜+二叉树）：P1364 医院设置 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include<bits/stdc++.h>
using namespace std;
int n,vis[105],total=1e9,ans;
struct node{int peo,l,r,f;}a[105];
struct hspt{int id,dis;};
queue<hspt>q;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i].peo>>a[i].l>>a[i].r;
        a[a[i].l].f=i;a[a[i].r].f=i;
    }
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        vis[i]=1;
        ans=0;
        q.push({i,0});
        while(!q.empty()){
            hspt tmp=q.front();q.pop();
            //父节点 
            if(a[tmp.id].f&&!vis[a[tmp.id].f]){
                ans+=a[a[tmp.id].f].peo*(tmp.dis+1);
                vis[a[tmp.id].f]=1;
                q.push({a[tmp.id].f,tmp.dis+1});
            }
            //左儿子 
            if(a[tmp.id].l&&!vis[a[tmp.id].l]){
                ans+=a[a[tmp.id].l].peo*(tmp.dis+1);
                vis[a[tmp.id].l]=1;
                q.push({a[tmp.id].l,tmp.dis+1});
            }
            //右儿子 
            if(a[tmp.id].r&&!vis[a[tmp.id].r]){
                ans+=a[a[tmp.id].r].peo*(tmp.dis+1);
                vis[a[tmp.id].r]=1;
                q.push({a[tmp.id].r,tmp.dis+1});
            }
            
        }
        total=min(ans,total);
    }
    cout<<total;
    return 0;
}

 三.二叉搜索树（BST）

1.BST性质

（1）左子树小于根，右子树大于根

（2）二叉搜索树的每一棵子树都是一颗二叉搜索树 

2.二叉树的查询

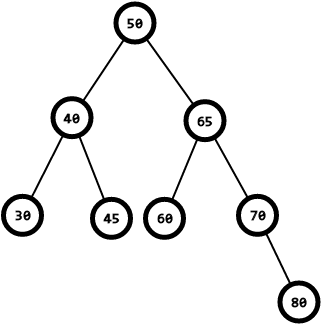
 根据二叉树的性质，如果根节点的数刚好是查找的数，则返回根节点的值；不然有两种情况，一是此数比根节点小，则查询此根左子树，二是此数比根节点大，则查询此根右子树。

例如上图，

我们要查询60

从根节点50开始，60 > 50 往右子树里找，到65，65 > 60 往右子树里找，找到60

3.二叉树的插入

与查询一样，依次判断寻找子树，直到叶子节点后加入此数。

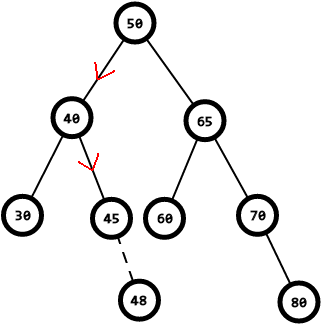
如图我们要插入48

48 < 50，去左子树，到40

48 > 40，去右子树，到45

48 > 45，45没有子节点了，48成为45的右儿子

4.二叉树的最值

最小值 >> 一直在左子树找

最大值 >> 一直在右子树找

5.二叉树的删除

在二叉树中，最好删除的是叶子结点，如此我们可以看此节点是否为叶子结点，如果不是，就在不破坏二叉树性质的前提下，将其与左/右节点交换位置，直到它成为叶子结点。

6.例题讲解

P5076 【深基16.例7】普通二叉树（简化版）

1.首先读题可知，题目中需要我们的操作是

（1）查询排名为x的数

（2）查询数x的排名

（3）求x的前驱与后继

（4）插入数x

ok，这样让我们一个个来讲解查看

首先，也是最重要的一点，我们先构建一棵二叉查找树

（1）造树

 普及一个小知识，结构体内连接初始值操作方法如下

struct Node{//此结构体有两个构造函数 
    int left,right,size,value,num;
    Node(int l,int r,int s,int v):left(l),right(r),size(s),value(v),num(1){ }//构造初始值 
    Node(){    }//无参默认构造函数 
}t[MAXN];

 

使用inline’关键字可以提高函数调用的效率，但它通常用于短小的函数，因为将函数内容嵌入到每个调用点可能会增加代码大小。在这里，它被用于、update’函数，因为这个函数的目的是在每个节点的更新中执行一些小的计算，内联它可以提高执行效率。

//左子树坐标下左子树大小 + 右子树坐标下右子树的大小 + 根节点的大小
inline void update(int root){
    t[root].size =t[t[root].left ].size +t[t[root].right ].size +t[root].num;//不断将每一个点的大小加入根节点并汇总 
    //更新节点信息 
}

汇总：所有的预备工作

struct Node{//此结构体有两个构造函数 
    int left,right,size,value,num;
    Node(int l,int r,int s,int v):left(l),right(r),size(s),value(v),num(1){ }//构造初始值 
    Node(){    }//无参默认构造函数 
}t[MAXN];
inline void update(int root){
    t[root].size =t[t[root].left ].size +t[t[root].right ].size +t[root].num;//不断将每一个点的大小加入根节点并汇总 
    //更新节点信息 
}

 

其次，我们先看最常用的查询操作

（2）查询

1.查询数x的排名

因为我们知道二叉树的性质，左子树中数都小于根，右子树中数都大于根，所以我们可以在查询中判断x是否大于根，又或是小于根，那么就在右/左子树中递归查找（注意如果在右子树中查找时记得将左子树大小加入答案），直到根就是左子树，输出答案即可。

int rank(int x,int root){//查找数x的排名
    if(root){//根中有叶子而不为0
        if(x<t[root].value)//如果此点小于根，则进入左子树查找 
            return rank(x,t[root].left);
        if(x>t[root].value)//如果此点大于根，则进入右子树查找 
            return rank(x,t[root].right+t[t[root].left ].size +t[root].num);
        return  t[root].num +t[t[root].left ].size ;//如果刚好查到其本身，则返回左子树与根的大小总和 
    } 
    return 1;//如果该树未有叶子，则直接返回值一 
}

2.查询排名为x的数

 此查找与上一段最显著的差别就是，这个是以排名查找树的值，而上一个是以树的值查找排名；

则此时则也有三种情况：

（1）x 这个排名比根节点排名小，则进入左子树

（2）x 这个排名比根节点排名大，则进入右子树，同时把 x 减去左子树的排名

（3）x 这个排名就是根节点排名，返回根节点的值

int kth(int x,int root){//查询排名为 x 的数
    if(x<=t[t[root].left ].size )return kth(x,t[root].left );//排名为x的数在左子树，故进入左子树 
    if(x<=t[t[root].left ].size +t[root].num )return t[root].value;//当前根节点为要找的数，直接返回 
    return kth(x-t[t[root].left ].size -t[root].num ,t[root].right );
    //排名为x的数在右子树，进入右子树并把x减去左子树 size+t[root].num(根节点).
}

 （3）插入

插入的规则很容易理解，首先判断插到哪棵子树，在递归寻找没有左或右子节点的树，新建后插入

记得每次插入后跟新节点总值

//插入的规则很容易理解，首先判断插到哪棵子树，在递归寻找没有左或右子节点的树，新建后插入
void insert(int x,int &root){
    if(x<t[root].value ){//是否在左子树中 
        if(!t[root].left)//是否有左子树 
            t[t[root].left=cnt++]=Node(0,0,1,x);//新建所需节点 
        else
            insert(x,t[root].left );//递归查询 
    }else if(x>t[root].value ){//是否在右子树中 
        if(!t[root].right ){//是否有右子树 
            t[t[root].right =cnt++]=Node(0,0,1,x);//新建节点 
        }else{
            insert(x,t[root].right );//递归查询 
        }
    }else{//如果根节点就是这个数 
        t[root].num ++;//根节点个数 
    }
    update(root); //更新此时节点信息 
} 

至此之上，便是这道题目主要考察的算法点了