牛客网刷题笔记篇
字符串篇
字符串翻转
import java.util.*;
public class Solution {
public String trans(String s, int n) {
// write code here
if (n == 0) return s;
StringBuffer stringBuffer = new StringBuffer();
char step = 'a' -'A';
for(int i = 0;i<n; i++) {
char c = s.charAt(i);
if(c >= 'a' && c <= 'z') {
stringBuffer.append((char) (c - step));
} else if (c >= 'A' && c <= 'Z') {
stringBuffer.append((char) (c + step));
} else {
stringBuffer.append(c);
}
}
stringBuffer = stringBuffer.reverse();
for(int i = 0; i< n;i++) {
int j = i;
while(j <n && stringBuffer.charAt(j) != ' ') {
j ++;
}
String temp = stringBuffer.substring(i, j);
StringBuffer sb = new StringBuffer(temp);
temp = sb.reverse().toString();
stringBuffer.replace(i, j, temp);
i = j;
}
return stringBuffer.toString();
}
}
思路: 先将字符串大小写转换; 然后翻转整个字符串,再以空格为界限,翻转每一个词
用到的java 的基本能力:
- StringBuffer 的reverse函数, 翻转一个字符串;
- 取字符串某个位置的字符: s.charAt(index). String 和StringBuffer 都有此方法
- 截取字符串,sb.substring(i, j)。 包括i不包括j。String和StringBuffer都有此方法
- 某区间字符串替换,StringBuffer 才有,sb.replace(i, j, temp);
Sting 的单个字符替换 或者 子串替换。s.replace('a', 'c'), 将s中的a替换为c。
replacing "aa" with "b" in the string "aaa" will result in "ba" rather than "ab". - 大小写转换 相差‘a’ -‘A’; 小写数值较大, c >= 'a' && c <= 'z' 则是小写
最长公共前缀,注意关键字 前缀
给你一个大小为 n 的字符串数组 strs ,其中包含n个字符串 , 编写一个函数来查找字符串数组中的最长公共前缀,返回这个公共前缀。
注意是前缀, 这个比最长公共字符串简单得多!!
import java.util.*;
public class Solution {
public String longestCommonPrefix (String[] strs) {
int n = strs.length;
//空字符串数组
if (n == 0)
return "";
//遍历第一个字符串的长度
for (int i = 0; i < strs[0].length(); i++) {
char temp = strs[0].charAt(i);
//遍历后续的字符串
for (int j = 1; j < n; j++)
//比较每个字符串该位置是否和第一个相同
if (i == strs[j].length() || strs[j].charAt(i) != temp)
//不相同则结束
return strs[0].substring(0, i);
}
//后续字符串有整个字一个字符串的前缀
return strs[0];
}
}
找出一个字符串中的最长连续重复字符
比如:“abcccdeef” 中,c连续出现3次,所以该字符串最长连续重复字符为c,长度为3.
// 最长连续重复子串
// abcccdeef 的最长连续子串为ccc,长度为3
// 用一个字符记录 对应的字符,一个数字记录出现次数
public static void maxRepeatCharLen() {
String s = "bcaddddefg";
int n = s.length();
int max = 1;
char targetChar = s.charAt(0);
int[] dp = new int[n];
dp[0] = 1;
for(int i = 1; i < n;i++) {
if(s.charAt(i) == s.charAt(i-1)) {
dp[i] = dp[i-1] + 1;
if(dp[i] > max) {
max = dp[i];
targetChar = s.charAt(i);
}
} else {
dp[i] = 1;
}
}
StringBuffer sb = new StringBuffer();
for(int i =0;i<max;i++) sb.append(targetChar);
Logger.i(" target chars is: " + sb + ", len: " + max);
}
一群字符串中的最长公共字符串(动态规划)
import java.util.*;
public class Solution {
/**
* longest common substring
* @param str1 string字符串 the string
* @param str2 string字符串 the string
* @return string字符串
*/
public String LCS (String str1, String str2) {
// write code here
// 动态规划: dp[i +1][j+1] = if(s[i] == s[j]) dp[i][j] + 1
int m = str1.length();
int n = str2.length();
int maxLen = 0, targetRightIndex = -1;
int[][] dp = new int[m +1][n+1];
for(int i = 0;i<m;i++)
for(int j = 0;j<n;j++) {
if(str1.charAt(i) == str2.charAt(j)) {
dp[i+1][j+1] = dp[i][j] +1;
if(maxLen < dp[i+1][j+1]) {
maxLen = dp[i+1][j+1];
targetRightIndex = i;
}
}
}
if(targetRightIndex == -1) return "";
return str1.substring(targetRightIndex - maxLen +1, targetRightIndex +1);
}
}
最小覆盖子串
- 描述
给出两个字符串 s 和 t,要求在 s 中找出最短的包含 t 中所有字符的连续子串。数据范围:0 \le |S|,|T| \le100000≤∣S∣,∣T∣≤10000,保证s和t字符串中仅包含大小写英文字母
要求:进阶:空间复杂度 O(n)O(n) , 时间复杂度 O(n)O(n)
例如:
S ="XDOYEZODEYXNZ"S="XDOYEZODEYXNZ"
T ="XYZ"T="XYZ"
找出的最短子串为"YXNZ""YXNZ".
注意:
如果 s 中没有包含 t 中所有字符的子串,返回空字符串 “”;
满足条件的子串可能有很多,但是题目保证满足条件的最短的子串唯一。
- 解题要点
- s中必须包含t中的所有字符,t中同一个字符出现两次,在s中也至少出现2次。如s = "ababa", t="aa"; 则结果为“aba”,而不是“a”。
- 既然有出现次数要求,最好使用map来统计一下t中字符出现的次数
- 配合滑动窗口法,在满足条件的子串中找最短的。
- 使用三个变量分别记录目标区间上下界,区间长度; 使用两个移动下标表示动态窗口的下标
import java.util.*;
public class Solution {
/**
*
* @param S string字符串
* @param T string字符串
* @return string字符串
*/
//检查是否有小于0的
boolean checkPass(int[] exist) {
for (int i = 0; i < exist.length; i++) {
if (exist[i] < 0)
return false;
}
return true;
}
public String minWindow (String S, String T) {
int n = S.length();
int[] tSet = new int[128];
int targetLeft = -1, targetRight = 0,
targetLen = n + 1; // 最优结果下标及长度
int fast = 0, slow = 0; // 动态窗口 下标
for (int i = 0; i < T.length(); i++)
tSet[T.charAt(i)] -= 1;
for (fast = 0; fast < n; fast++) {
tSet[S.charAt(fast)] += 1;
// 在满足条件的区间内缩小范围
while (checkPass(tSet)) {
if (targetLen > fast - slow + 1) {
// 更新最短区间及长度
targetLen = fast - slow + 1;
targetLeft = slow;
targetRight = fast;
}
// 左移区间之前,需要将对应位置的标记减一
tSet[S.charAt(slow)]--;
slow ++;
}
}
if (targetLeft == -1) {
return "";
} else {
return S.substring(targetLeft, targetRight + 1);
}
}
}
括号匹配-求最长合法括号长度
- 描述
给出一个长度为 n 的,仅包含字符 '(' 和 ')' 的字符串,计算最长的格式正确的括号子串的长度。
例1: 对于字符串 "(()" 来说,最长的格式正确的子串是 "()" ,长度为 2 .
例2:对于字符串 ")()())" , 来说, 最长的格式正确的子串是 "()()" ,长度为 4 .
例子: "(((()())" ,最长正确格式子串为"(()())" ,长度为6
- 分析:
这个问题是匹配问题,完全可以使用栈的结构,左括号入栈,右括号出栈;如果右括号时栈为空,说明括号非法,此位置之前得已经完成匹配了,加上这个肯定不是合法得,所以起始位置需要从下一个位置开始。
如果右括号时非空,则pop栈顶,说明之前肯定有左括号。
import java.util.*;
public class Solution {
/**
*
* @param s string字符串
* @return int整型
*/
public int longestValidParentheses (String s) {
// write code here
int n = s.length();
int maxLen = 0;
int start = -1;
Stack<Integer> stack = new Stack<Integer>();
for(int i = 0;i<n;i++) {
if(s.charAt(i) == '(') {
stack.push(i);
} else {
//非法括号,括号不可能是右括号开头
if(stack.isEmpty()) {
start = i;
} else {
stack.pop();
if(stack.isEmpty())
maxLen = Math.max(maxLen, i-start);
else
maxLen = Math.max(maxLen, i-stack.peek());
}
}
}
return maxLen;
}
}
滑动窗口法
最长‘无重复’子数组,最长无重复子串
题目地址
最长无重复子数组,最长无重复子串,都是类似, 使用两个指针维持一个窗口.
用一个集合来存储当前不重复的子数组,对于每一个新元素:
如果新元素不在集合出现,则将其加入集合,right 右移, 并更新最长的长度maxLen和对应的右边界下标;否则,left 右移,集合中删掉最左边的数据,也就是从窗口左边界右移。
//滑动窗口法,维护两个指针
public static void maxUniqueSubArrLen() {
int[] arr = {1,2,4,5,2,4,6,7,2,1};
int n = arr.length;
int maxLen = 0, endIndex = 0;
HashSet<Integer> set = new HashSet<>();
int left = 0,right = 0;
while(right < n) {
if(set.contains(arr[right])) {
set.remove(arr[left]);
left++;
} else {
set.add(arr[right++]);
// 这样还可以记录下最后的目标数组结果
if( maxLen < set.size()) {
maxLen = set.size();
endIndex = right; // 记录最长串时的右下标
}
}
}
Logger.i(" len: " + maxLen);
StringBuffer sb = new StringBuffer();
for (int i = endIndex - maxLen; i< endIndex;i++){
sb.append(arr[i] +" ");
}
Logger.i(" sub arr is: " + sb);
}
动态规划
楼梯系列
青蛙跳楼梯
描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
public class Solution {
public int jumpFloor(int target) {
// 递推公式:f(n) = f(n-1) + f(n-2)
// 第n个台阶要么是从n-1 + 1 而来; 要么是n-2 +2
if(target < 3) return target;
int f1= 1, f2 = 2, f3 = 3;
for(int i=3;i<=target;i++) {
f3 = f1 + f2;
f1 = f2;
f2 = f3;
}
return f3;
}
}
最小花费爬楼梯
描述
给定一个整数数组 , cost[i] 是从楼梯第i个台阶向上爬需要支付的费用,下标从0开始。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
题目地址
思路: dp问题,
- 首先找到递推公式 fn = min(f(n-1) + cost[n-1], f(n-2) + cost[n-2]);
- 找到初始值 和终止条件
- 循环递推
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param cost int整型一维数组
* @return int整型
*/
public int minCostClimbingStairs (int[] cost) {
// write code here
// fn = min(f(n-1) + cost[n-1], f(n-2) + cost[n-2])
int n = cost.length;
int f0 = 0, f1 = 0, f2 = Math.min(f1 + cost[1], f0 + cost[0]);
for(int i = 2; i<=n; i++) {
f2 = Math.min(f1 + cost[i-1], f0 + cost[i-2]);
f0 = f1;
f1 = f2;
}
return f2;
}
}
偷东西1,不能偷连续两间房
- 描述
你是一个经验丰富的小偷,准备偷沿街的一排房间,每个房间都存有一定的现金,为了防止被发现,你不能偷相邻的两家,即,如果偷了第一家,就不能再偷第二家;如果偷了第二家,那么就不能偷第一家和第三家。
给定一个整数数组nums,数组中的元素表示每个房间存有的现金数额,请你计算在不被发现的前提下最多的偷窃金额。
数据范围:数组长度满足 1≤n≤2×10^5,数组中每个值满足 1≤num[i]≤5000.
- 分析
这是一个典型得动态规划得问题,其实大体有取有舍得这种问题,大体都可以认定为动态规划问题。
我们来分析有n分房间的最大值:f(n), 它要么是f(n-2) 上来的,要么是f(n-1) 直接放弃偷n。
所以递推公式: f(n) = max(f(n-2) + a[n], f(n-1))
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @return int整型
*/
public int rob (int[] nums) {
// write code here
//f(n) = max(f(n-1), f(n-2) + a[n])
int sum = 0;
int n = nums.length;
if(n == 1) return nums[0];
if(n == 2) return Math.max(nums[0], nums[1]);
int f1 = nums[0];
int f2 = Math.max(nums[0], nums[1]);
int f3 = 0;
for(int i =2;i<n;i++) {
f3 = Math.max(f1 + nums[i], f2);
f1 = f2;
f2 = f3;
}
return f3;
}
}
偷东西2,相邻不能同时偷,首尾相邻
-
描述
你是一个经验丰富的小偷,准备偷沿湖的一排房间,每个房间都存有一定的现金,为了防止被发现,你不能偷相邻的两家,即,如果偷了第一家,就不能再偷第二家,如果偷了第二家,那么就不能偷第一家和第三家。沿湖的房间组成一个闭合的圆形,即第一个房间和最后一个房间视为相邻。
给定一个长度为n的整数数组nums,数组中的元素表示每个房间存有的现金数额,请你计算在不被发现的前提下最多的偷窃金额。
数据范围:数组长度满足 1≤n≤2×10^5,数组中每个值满足 1≤num[i]≤5000. -
分析
这个题和上面一个是一样的,区别在于这题多了个条件: 首尾不能同时偷。
所以我们把情况分为两种:- 偷了首家的,此时它不能偷最后一家,所以循环时需要把最后一家去掉,相当于求f(n-1)
- 没偷首家,此时它能够偷最后一家,那么循环时带上最后一家就行了,相当于从第二项开始到最后求最大值。
然后两种情况中取较大者就行了。
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @return int整型
*/
public int rob (int[] nums) {
// write code here
// 这个是典型的动态规划问题,dp[n] = max(dp[n-1], dp[n-2] + a[n-1])
//但是多了一个条件是:首位不能同时选,那么我分为两种情况选择出最大的就行了
int n = nums.length;
int maxValue = 0;
int [] dp = new int[n+1];
// 选择了选择了首个的
dp[1] = nums[0];
for(int i =2; i< n;i++) {
dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
}
maxValue = dp[n-1];
Arrays.fill(dp,0);
// 不选首个的
dp[1] = 0;
for(int i = 2;i<=n;i++) {
dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
}
maxValue = Math.max(maxValue, dp[n]);
return maxValue;
}
}
矩阵的最小路径和
- 题目描述
给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。
要求:时间复杂度 O(nm)O(nm)
例如:当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时,对应的返回值为12,
所选择的最小累加和路径如下图所示:
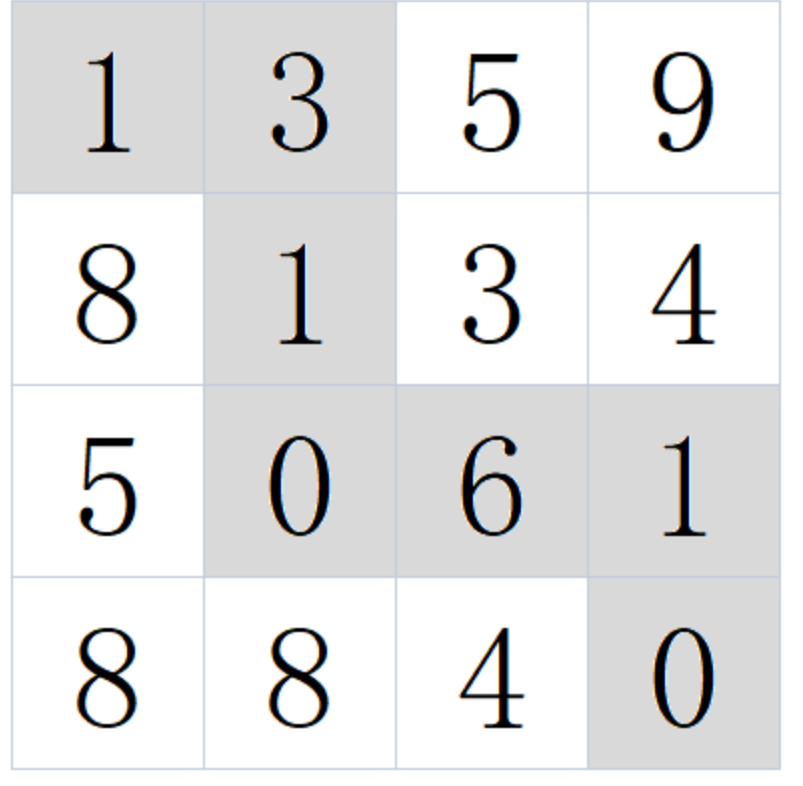
- 分析
动态规划问题,先拆解子问题,第i,j 位置的最小路径, 只能是它上一个来的,或者左边来的。所以递推公式: dp[i][j] = a[i][j] + min(dp[i-1][j], dp[i][j-1]);
注意初始条件:
第一行:dp[0][i] = sum(a[0][0]...a[0][i])
第一列:dp[j][0] = sum(a[0][0]...a[j][0])
import java.util.*;
public class Solution {
/**
*
* @param matrix int整型二维数组 the matrix
* @return int整型
*/
public int minPathSum (int[][] matrix) {
// write code here
//f(i,j) = f(i-1,j-1) + min( a[i-1,j], a[i][j-1])
int m = matrix.length;
int n = matrix[0].length;
int[][] dp = new int[m][n];
int sum = 0;
for(int i = 0;i<m;i++) {
sum+= matrix[i][0];
dp[i][0] = sum;
}
sum = 0;
for(int j=0;j<n;j++){
sum += matrix[0][j];
dp[0][j] = sum;
}
for(int i = 1;i<m;i++)
for(int j = 1;j<n;j++) {
dp[i][j] = matrix[i][j] + Math.min(dp[i-1][j], dp[i][j-1]);
}
return dp[m-1][n-1];
}
}
最长、最短子序列系列
最长严格上升子序列
给定一个长度为 n 的数组 arr,求它的最长严格上升子序列的长度。
所谓子序列,指一个数组删掉一些数(也可以不删)之后,形成的新数组。例如 [1,5,3,7,3] 数组,其子序列有:[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。
我们定义一个序列是 严格上升 的,是指严格递增。
题目地址
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 给定数组的最长严格上升子序列的长度。
* @param arr int整型一维数组 给定的数组
* @return int整型
*/
public int LIS (int[] arr) {
// write code here
// 一个元素是严格上升子序列,只需不断往里面加元素且保证是严格上升子序列就行
// 对于每一个到i结尾的子数组,如果遍历过程中遇到元素j小于i处元素,说明以j元素结尾的子序列加上子数组末尾元素也是严格递增的,因此转移方程: dp[i] = dp[j] +1
int n = arr.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
int maxLen = n < 2 && n >= 0 ? n : 0; // 边界条件
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
// 说明递增,且i 拼接在j处达到最长
if (arr[i] > arr[j] && dp[i] < dp[j] + 1) {
dp[i] = dp[j] + 1;
maxLen = Math.max(maxLen, dp[i]);
}
}
}
return maxLen;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号