[Entertain] 证明 SCPTT D2T1

[Entertain] 证明 SCPTT D2T1

性质：对于一个有解的串 \(S\)，对于所有 \([l,r]\)，满足 \(f([l,r])=f([\lvert S\rvert-r+1,\lvert S\rvert-l+1])\)

Part 1. 对称子串的有解性是相同的

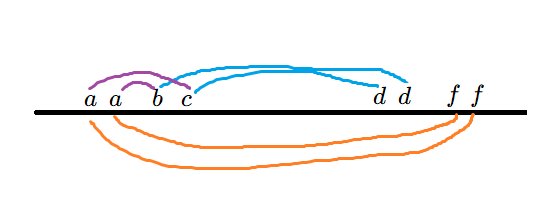
考虑反证法，假设两个对称子串的有解性不是相同的，不妨设左边那个区间无解，右边的有解。如图设左边的情况是 \(a\) 分别与 \(b,c\) 对应，其中 \(b\neq c\)，由于整个字符串是有解的，所以左边的两个 \(a\) 对应的右边的数必须相同，设为 \(f\)，由于假设说右边是有解的，那么右边 \(f\) 对应的只能是一种数，设为 \(d\)，显然，\(b,c\) 与 \(d\) 是在 \(S\) 中对应的，那么 \(S\) 无解，矛盾，故假设不成立。

Part 2. 对称子串的答案是相同的

我们只需要说明对称的子串出现的数的种类数是相同的即可，显然，因为 \(S\) 有解，所以 \(S\) 中出现的数要么和自己配对，要么和另一个数互相配对，所以一定同时给两边的子串加一个相同的数或者分别加一个不同的数，种类是相同的。

Part 3. 暴力移动指针的时间复杂度

本题不好直接计算答案，只能暴力移动指针来计算答案，然而这个的复杂度是对的，感觉套用到 Z 函数上面去也是可以的（？