[Note] 决策单调性优化 DP

[Note] 决策单调性优化 DP

Preface：

与 wqs 二分网络资料的晦涩难懂相比，决策单调性优化的 OI Wiki 页面写得很好，因此本文只是一些补充，对于定义或者是某些严格证明，请参见 四边形不等式优化 - OI Wiki (oi-wiki.org)。

Part 0. 二分队列怎么写不容易错

下为 Lightning Conductor 代码

struct Node{int x,l,r;Node(int _x=0,int _l=0,int _r=0):x(_x),l(_l),r(_r){}};
deque<Node> dq;
double w(int j,int i){return a[j]+sqrt(i-j)-a[i];}
bool better(int a,int b,int t){return w(a,t)>w(b,t);}//最小转移点
void Solve(){
    dq.clear(),dq.push_back(Node(1,1,n));
    for(int i=1;i<=n;i++){
        while(!dq.empty() and dq.front().r<i) dq.pop_front();
        if(!dq.empty()) dq.front().l=i;
        while(!dq.empty() and better(i,dq.back().x,dq.back().l)) dq.pop_back();
        if(dq.empty()) dq.push_back(Node(i,i+1,n));
        else if(better(i,dq.back().x,dq.back().r)){
            int l=dq.back().l,r=dq.back().r,mid,res=0;
            while(l<=r){
                mid=(l+r)/2;
                if(better(i,dq.back().x,mid)) res=mid,r=mid-1;
                else l=mid+1;
            }
            dq.back().r=res-1,dq.push_back(Node(i,res,n));
        }else if(dq.back().r<n) dq.push_back(Node(i,dq.back().r+1,n));
        ans[i]=max(ans[i],(int)ceil(w(dq.front().x,i)));
    }
}

Part 1. 一个性质和有趣的题目 / 部分利用决策单调性

基于二阶混合差分的特点，这样的函数：

\[f(i)=\min_{1\le j\le i}\{F(i)+G(j)+w(j,i)\} \]

若 \(w(j,i)\) 满足四边形不等式，那么 \(F(i)+G(j)+w(j,i)\) 也满足四边形不等式，通过它的定义可以看出（两边同时消去）。而 \(F(i),G(j),w(j,i)\) 都可以与 \(f(i)\) 有关或无关，这对它是不是满足四边形不等式无关，我们只需要保证它能够被消掉，切勿递归地展开这些函数，而是把他们看作是一个已经计算出的其他数列，否则可能认为这是一个相当反直觉的结论。

由此，\(f(i)=g(i)\circ \min_{1\le j\le i}\{F(i)+G(j)+w(j,i)\}\) 中的 \(f(i)\) 可以用决策单调性来优化，而与 \(g(i),F(i),G(j),w(j,i)\) 是否互相包含无关，只要有正常的转移顺序即可，其中 \(\circ\) 是某种将两个函数的结果复合的方式。这一切都只需要 \(w(j,i)\) 满足四边形不等式，因为无论还有何种转移，\(f(i)\) 的值等于什么，都不影响后面这个转移的决策单调性。

由此，我们可以用其他方式计算前者的转移，用二分队列法依次求出后面这部分的值。其实这与区间分拆问题的原理没什么两样。

例题 我是奶龙 U560899 by lupengheyyds & way.exe

给定 \(n,k\) 且 \(0\le k\le 500,1\le n\le 10^5\)，求一个序列 \(\{1,2,3,\dots,n\}\) 的划分，最小化每一段的权值之和，一段的权值的定义如下，其中 \(\oplus\) 代表按位异或：

\[f(\{l,l+1,\dots,r-1,r\})=\begin{cases} l^6\oplus r^5 & r-l+1\le k\\ (r^2-l)^3 & \texttt{otherwise} \end{cases} \]

注意 \((r^2-l)^3\) 满足四边形不等式，暴力计算前者，用二分队列计算后者即可。

Part 2. 反四边形不等式与交错路

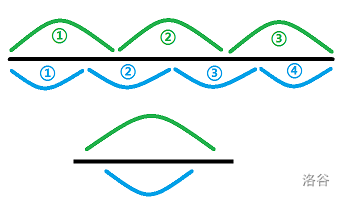
(from @command_block)

在没有区间个数限制的区间分拆问题里，若存在决策单调性，增多一个区间显然会形成如图上面部分的转移，而不会出现下面这样的，这个结论仅是部分满足四边形不等式。

To be continued