[Entertain] 证明 20250404 T1 之 容易发现

[Entertain] 20250404 T1 之 "容易发现"

一个序列 \(a\)，若长度为 \(n\)，冒泡排序（递增） \(k\) 轮之后，前 \(i\) 个数会变成原序列前 \(\min(i+k,|a|)\) 个数中较小的 \(i\) 个。

先对于 \(k=1\) 说明。我们知道一个序列中最大的数在一轮排序之后就会归位，设这个数原先在 \(i\) 位置。那么我们只需要说明 \(i\sim n\) 这几个位置是满足的即可，因为归位了这个数之后 \(a_{1\sim (i-1)}\) 就会做类似的操作，即选择一个 \(1\sim i-1\) 中的最大值然后提到 \(a_{i-1}\)。由于 \(a_i\) 会被归到 \(a_n\)，显然是成立的。

考虑归位第 \(k\) 大之前，设这个数它现在在 \(a_i\)，假设对于所有小于 \(k\) 的排序轮数，这个性质都满足。

对于 \(i\in(n-k,n]\)，这条规律是满足的，因为此时 \(i+k\ge n\)，前 \(k\) 大的数已经放在了现在的 \(a_{n-k+1\sim n}\) 处。

现在对于 \(i\le n-k\) 证明。我们也只要对于现在的 \(a_{i\sim n-k}\) 证明这个结论在排了 \(k\) 轮的时候成立，对于 \(j\in[i,n-k]\)：

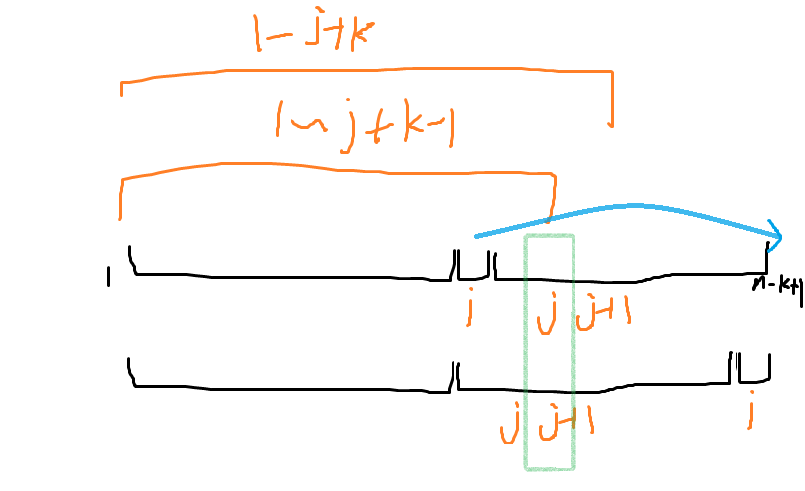
由归纳假设，现在的 \(a_{1\sim j+1}\) 是原序列 \(1\sim j+k\) 中的前 \(j+1\) 小的，由假设，\(i\) 是原先序列第 \(k\) 大的，也就是现在序列前 \(n-k+1\) 个中最大的那个，也就是说，现在序列的 \(a_i\) 是原先序列 \(1\sim j+k\) 中第 \(j+1\) 小的。现在把这第 \(i\) 个数归位到第 \(n-k+1\) 个位置上，原先组成 \(1\sim j+1\) 的序列平移到了 \(1\sim j\)，由于唯一缺少的一个数，即现在序列的 \(a_i\)，是原先序列前 \(1\sim j+k\) 中第 \(j+1\) 小的数，那么现在组成 \(1\sim j\) 的数就是原序列中前 \(j\) 小的。\(\square\)