[Entertain] 2025.04.17 T1 贪心证明

[Entertain] 2025.04.17 T1 贪心证明

考试的时候使用了一个贪心算法，现在试证其正确性。

Part 1. 贪心过程

深度优先遍历整棵树，回溯时，重复执行：从子树中找一个提上来之后收益最大的棋子，重复操作直到找不到为止。

Part 2. 正确性证明

采用决策包容性证明贪心策略，由于是从下往上选取的，依次考虑以下情况：

• 放到了应该放的位置

  那么由于选的是收益最大的，此时是正确的

• 没有放到应该放的位置

  此时只有一种可能即这枚棋子应该继续被往上提，由于是从下往上操作的，直接提到上面和继续往上提的效果是一样的，所以当前决策之后不会减少后续的决策空间。\(\square\)

Part 3. 时间复杂度

Acknowledgement: @nie_zy

称一个位于 \(i\) 的棋子具有的代价是 \(f_ic_i^2-f_i(c_i-1)^2=2f_ic_i-f_i\)，其中 \(c_i\) 表示当前有多少棋子在这个点上。一个点若是现在有 \(c_i\) 个棋子，那么提上一个棋子就要花上 \(f_i(c_i+1)^2-f_ic_i^2=2f_ic_i+f_i\) 的代价，由于提子的时候当前点肯定只有一个棋子（从下往上的），那么要花的代价依次就是 \(1f_i,3f_i,5f_i,7f_i,\dots (2k+1)f_i\) 这样。只要 \(2f_ic_i+f_i\le 2f_jc_j-f_j\) 就可以考虑把 \(j\) 处的子提到 \(i\) 处。显然上文提到的两个代价本质是相同的。

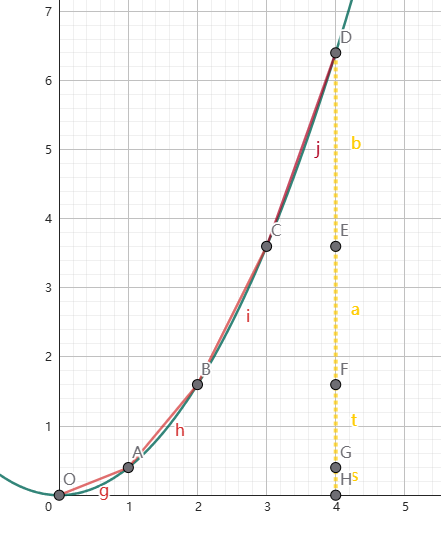
如图，每条黄色线段代表了一个棋子在此处的代价。显然，答案等于各棋子代价之和，我们每提一次棋子就会减少它的代价，所以我们现在估计一下它减少的速度。

我们考虑 \(i\) 点的子树，假设在这一处上提了 \(k\) 个棋子，那么他们的代价就变成了 \(1f_i,3f_i,5f_i,7f_i,\dots (2k+1)f_i\)。提子的条件是：放到 \(i\) 点的代价更小。由于提子的时候是从代价大的开始提的，因此，我们可以知道原先子树内棋子的代价至少是 \((2k+1)f_i\)。

上面这个数列是一个等差数列，它至少有 \(\frac{k}2=\mathcal O(k)\) 个数小于 \(k\)，也就是新替换的点有 \(\mathcal O(k)\) 个替换后代价小于 \(kf_i\)，所以，这部分棋子代价至少减少了一半。

最开始每个点只有一个棋子，每个棋子的代价最大是 \(V=10^{12}\)，这意味着每一个棋子能被提 \(\mathcal O(\log V)\) 次，因此，我们说明提子的次数界是 \(\mathcal O(n\log V)\)，总复杂度是 \(\mathcal O(n\log n\log V)\)。\(\square\)