[Entertain]2025.04.16 T3 证明

[Entertain]2025.04.16 T3 证明

若 \(G=(V,E)\) 是一张 \(3n\) 个点 \(m\) 条边的简单无向联通图，现在求 \(V\) 的一个划分 \(V_1,V_2,V_3\) 满足 \(V_1\cup V_2\cup V_3=V\)，且两两之间没有交，并且满足下面三条性质中的至少两个：

1. \(\left|V_1\right|=\left|V_2\right|=\left|V_3\right|\)

2. 图 \(G'=(V,E\setminus\{(u,v)\vert \exists i,u\in V_i\land v\in V_i\})\) 联通，换言之，如果在 \(G\) 中删除两个端点都属于同一个划分中的边，图还联通。

3. 对于所有 \((u,v)\text{ which }u,v\in V_i\) 有 \(\left|V_i\right|<\max_{i=1,2,3}\left\{\left|V_i\right|\right\}\)，换言之，大小最大的 \(V_i\) 中不能有边。

如果无解，输出 NO

事实上，不可能无解，我们给出如下的构造方法：

现在就说明它的正确性。

Part 1. 对于情况一

设两个部分的点数分别是 \(n\le a,b\le 2n\)。当选了一个奇数/偶数点集里面的点放到第三个部分之后，其父亲，一个一定在另一个集合里面的点，就不能被放到第三个集合里面了。那么，最坏情况下，每个点集都会少掉一部分点，\(a\to a-(b-n),b\to b-(a-n)\)。那么为了保证剩下的点仍然足够凑出第三部分，则要满足：

\[b-(a-n)\ge b-n \]

\[a-(b-n)\ge a-n \]

化为 \(2n\ge a,2n\ge b\)，这就是情况一的条件，当然成立。\(\square\)

Part 2. 对于情况二

不妨设两个点集的点数分别是 \(|a|<n,|b|>2n\)，那么考虑每一个 \(a\) 集合里面的点都会向 \(b\) 集合里面贡献一条边，使得 \(b\) 中某些点不能成为叶子节点，由于我们期望叶子节点尽量多（为了超过其他两个集合，满足性质 3），在最坏情况下，\(a\) 中每一个点都使得 \(b\) 中一个点不能成为叶子，还剩 \(|b|-|a|\) 个叶子。

由于 \(|a|<n,|b|>2n\)，一定有 \(|b|-|a|>n\)，从 \(b\) 中取出 \(|b|-|a|\) 个叶子成为第三部分，则 \(b\) 中还有 \(|a|\) 个点，由于 \(|a|<n\) 又 \(|b|-|a|>n\)，则 \(|b|-|a|>|a|\)，则第三部分严格大于剩下两个部分的大小。\(\square\)

Part 3. Bonus

如果第一种情况的判断条件不取等，而第二种判断条件取等，你能构造一组 Hack 数据吗？

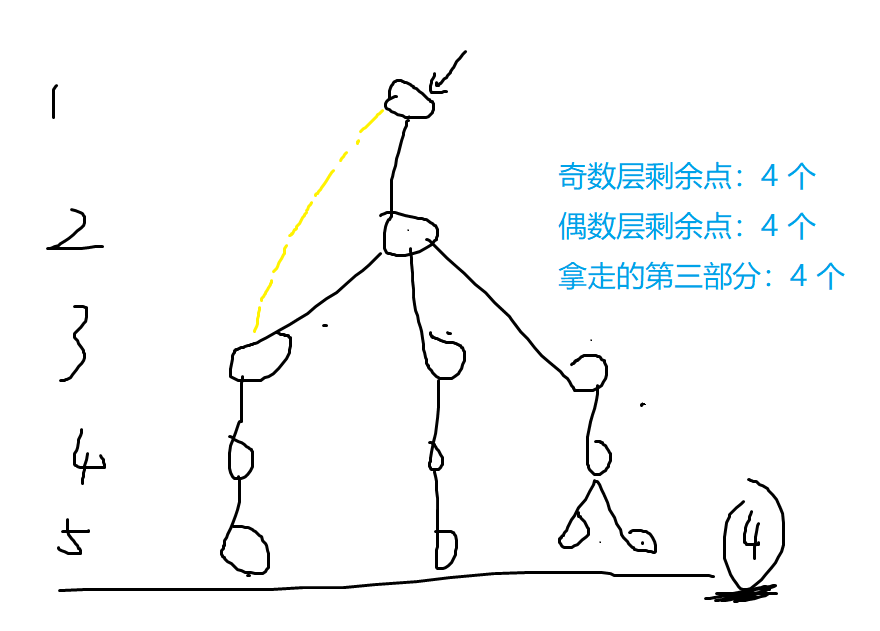
这种情况下，我们会拿走 4 个叶子作为第三部分，然而它并没有严格大于奇数层，所以，当存在如图黄色的非树边的时候，奇数层不是独立集，但是它的大小也是最大的，这不符合性质三，构造失败。当然，本图的情况恰满足性质 1,2，读者可以另行构造。