Visual Solution of 20250220

Visual Solution of 20250220

Graph

Sum

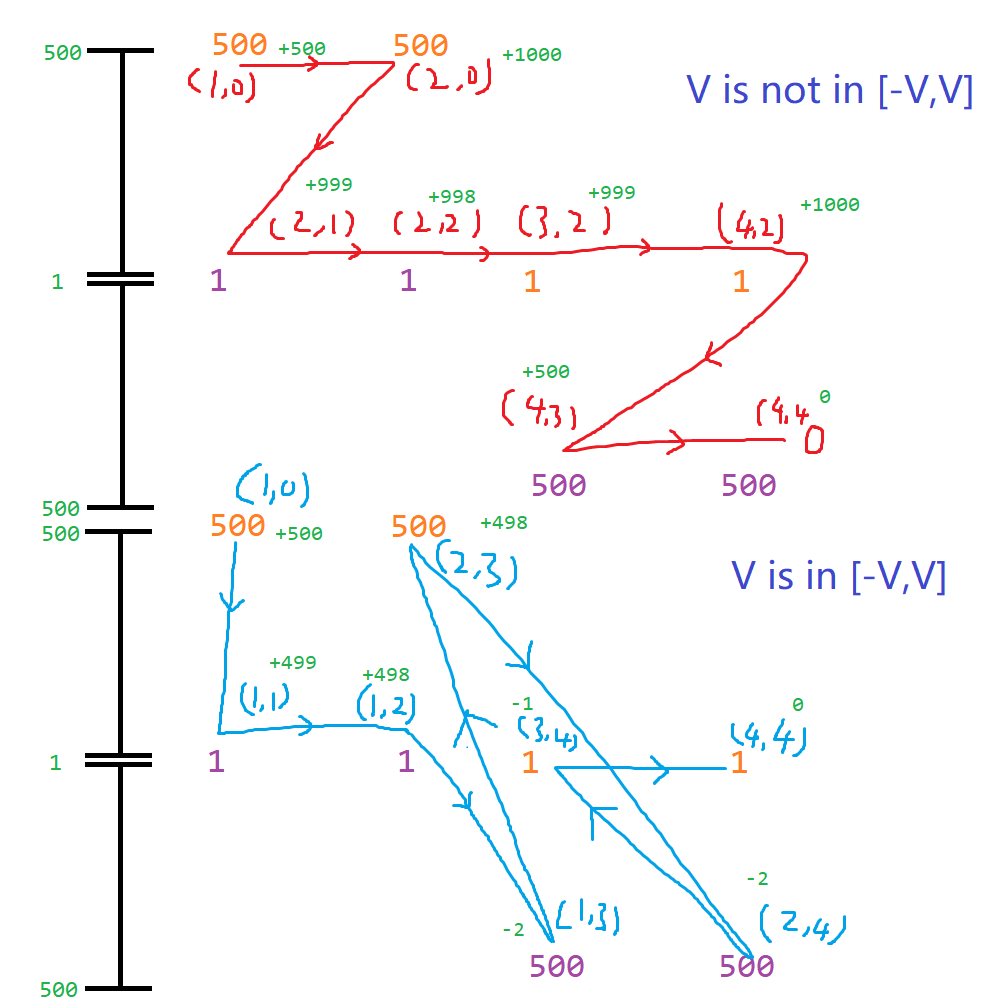
Path

最小化

\[\sum x_i \]

满足约束

\[\sum_{e\in P}x_e+w_e\ge c+d \]

\(d\) 是最短路

---

化为标准型

最大化

\[\sum -x_i \]

满足约束

\[\sum_{e\in P}-x_e \le \sum_{e\in P}w_e-c-d \]

---

对偶

最小化

\[\sum_{P}{\left(\sum_{e\in P}w_e-c-d\right)y_P} \]

满足约束

\[e:\sum_{P}-[\textbf{edge } e \text{ is in } P]y_P\ge -1 \]

---

化为标准型

最大化

\[\sum_{P}{\left(c+d-\sum_{e\in P}w_e\right)y_P} \]

满足约束

\[e:\sum_{P}[\textbf{edge } e \text{ is in } P]y_P\le 1 \]

---

另一种建模，可以直接用单纯刑法，加上 Subtask1 可得到 70pts：

最小化

\[\sum x_i \]

满足约束

\[(u,v):d[v]\le d[u]+w(u,v)+x_i \]

\[d[1]=0 \]

\[d[n]\ge c+d \]