lg-数学强行多合一

lg-数学强行多合一

线性代数

• 标准高斯消元

• 扩展的高斯消元

下面图中，有一行是全0行，没有主元，第二列也没有主元，这说明第二个元无法解出来，可以将其表示成一个未知数。

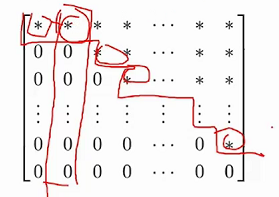
• CF832E

结果就是求模5意义下方程的解，若有 \(k\) 个自由元，则答案可以有 \(5^k\) 个

由于要做多次系数相同的高斯消元，可以把所有右边都合成一个来做

• 用高斯消元解决有后效性的 dp

显然应该先求每一条边的期望经过次数，最后给全部边贪心地赋予权值。

然后每一条边的期望次数可以通过端点的期望到达次数推出来，要计算期望到达次数，可以使用高斯消元。

• CF446D

\(x\overset{1/deg_x}{\to} y\overset{g_{y,j}}{\to} j\)

• CF1823F

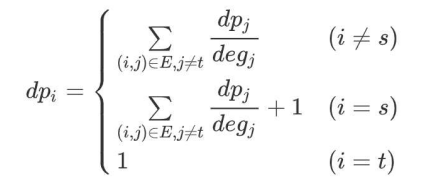
树上的高斯消元问题，可以分儿子父亲考虑，拆开之后只需要 \(\mathcal O(n)\)

• 线性基

有趣的东西：两个整数在算术加与数乘下的线性空间中最小的正整数是他们的最大公约数。

线性空间的大小显然为 \(2^{\operatorname {dim}(S)}\) ，\(\operatorname {dim}(S)\) 小于等于向量的维数。

显然在基里面，每一个主元的更高位显然为 0 （阶梯形矩阵），如果要插入的向量，其中一个主元为 0，这就意味着不能消去

• 两个已做过的例题

1. 线性基满足可重复贡献

2. 可以做树上线性基（利用时间戳）

3. 路径异或可以表达为简单环异或和一条链

• CF724G

【!REPLAY!/!LOOK_SOLUTION!】

• 行列式

倍加操作行列式不变。交换操作行列式变号。阶梯型矩阵行列式为主对角线数相乘。

• P4336 [SHOI2016]

容斥又出来攻击我。。。

• P6624 [省选联考 2020]

莫比乌斯反演又出来攻击我。

博弈论

• NIM

根据 SG 定理显然。

• 阶梯NIM

如果移动了偶数，那么下一步后手也可以把这些再移回偶数，换言之只要动了偶数上的，后手显然也能动一次，所以偶数上的都没有用。

• P5363

显然等价于阶梯Nim游戏，则考虑计数所有奇数个空白位置异或起来不为0的方案，然后塞一个插板法。

• [!REPLAY!]

• 不能用 SG 的问题

• AGC010D

[!REPLAY!]

计算坤何

• 点积：求夹角、求投影

• 叉积：求四边形面积、判断左右关系、判断点是否在直线/线段 AB 上、判断是否有交点、计算点到直线距离、计算交点坐标、判断平行

• NBNBNB