lg-math4
lg-math4
【!REPLAY!】
- 前缀和优化 \(f=g*1\)
可看作 \(n\) 个质因数,做高维前缀和

这个实例让我们知道实际上高维前缀和不一定只适用于 0/1
- 高维差分优化 \(f=g*\mu\)
由于 \(\mu*1=\epsilon\)
- 例子
Trick1:用莫比乌斯反演就是将 \(f=g*1\)
此时我们可以令 \(f=g*1\) 就可以把函数的复合放到外面。
然后考虑反演 \(f*\mu=g\)
- 例子2
\[\sum_{i=1}^{n}\sum_{j=1}^n\operatorname{lcm}(i,j) \]\(n\le 10^7\)
Trick2:经典拆 lcm、经典枚举 gcd、经典枚举因数、经典调换求和顺序(艾弗森法则)
Trick3:\([n=1]=\sum_{d|n}\mu(d)\)
注意整除分块套整除分块的复杂度为 \(\mathcal O(n)\)
同时也可以用上面例子1的方法令 \(F=\frac{1}n,F=g*1\)
用 \(g\) 替换后可得:
要快速求出 \(\sum_d g(d)\) 可利用线性筛 \(F*\mu=g\)
可以先乘上 \(n\) 然后化为一个简单的形式,然后可得出线性筛的做法。
- 例子3
唯一的不同就是 lcm 里面换掉了,可以考虑转化问题,不要枚举下标,而是枚举值,乘上出现次数。
- 例子4
Trick4:辗转相除转化过大 gcd
【!REPLAY!】 筛讨论
- 例子5
Trick5: 偏序关系难处理,化为等于关系,进行递推
令 \(G(n)=\sum_{i}^{n}\sum_{j}^{n}[\gcd(i,j)+\operatorname{lcm}(i,j)=n]\)
这里采用枚举 gcd 的方法。
那么后面这个式子有组合意义。可以筛出质因子数目。
Trick6: 提取公约数尽量去掉限制,注意艾弗森约定的组合意义。
- 基本和组
令 \(D(x)=\{\lfloor x/1\rfloor,\lfloor x/2\rfloor,\dots,\lfloor x/x\rfloor\}\)
通过分类讨论 \(\sqrt x\) 得到 \(\mathcal O(|D(x)|)=\mathcal O(\sqrt x)\)

定理 \(D(\lfloor x/a\rfloor)\subset D(x)\)
那么,计算一个卷积,如果可以知道其中一个函数的前缀和,则可以 \(\sqrt n\) 地求出卷积。不过,我们必须求前缀和。
- 杜教筛
现在要求 \(f\) 的前缀和
我们要找到 \(h=f*g\) ,构造出 \(h,g\) ,必须能 \(\mathcal O(1)\) 求前缀和。

即得杜教筛公式。
我们设定一个阈值 \(B=n^{2/3}\) ,小于的时候线性筛,大于的时候杜教筛。
- 神秘 Trick

下面还有两个神秘拆分
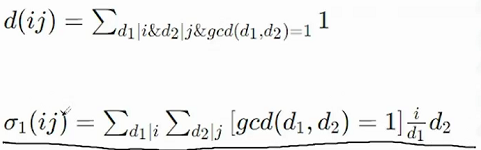
要证明只要证明在质数幂上是一样的就可以了
- Powerful Number 筛

注:因为对于所有正整数,都可以写成 \(2k+3\) 的形式

所以可以证明 \(\sigma\) 在质数处为 0 ,又由于积性,可以得到以上结论
最后得出公式是跟杜教筛公式的过程是一样的。
不过, \(\sigma\) 只在 Powerful Number 处有值,所以其复杂度是 \(\mathcal O(\sqrt n)\) 的。我们可以用展开卷积的方式

解出所有在质数幂的 \(\sigma\) ,就得到了所有 \(\sigma\)
至于 Powerful Number 的个数界,emm
重要性质(怎么这个时候才写):积性函数 \(f\) ,必有 \(f(1)=1\)
本文来自博客园,作者:haozexu,转载请注明原文链接:https://www.cnblogs.com/haozexu/p/18360138


 浙公网安备 33010602011771号
浙公网安备 33010602011771号