动态规划总结【分类2-DP优化】

动态规划总结【分类2-DP优化】

1 状态压缩

状态压缩，是从状态的表示入手的。在这样的问题中，我们常常可以抽象出一个表示答案必须的内容：一个数组，表示是否走过/当前状态。通常这种数据都只有两种类型。这个时候，就可以看看数据范围，判断是否使用状态压缩。

所以状态压缩省空间，主要是因为本来就没必要开那么多，省时间是因为它把原来需要O(N)

遍历的数组转化成可以O(1)计算的位运算

2 倍增优化

这个ST算法，可以说就是一种倍增优化DP

倍增优化主要是利用2的次幂的性质，把原来需要一个一个推的状态表示成2的次幂，这样提升了运算速度。

然后要求答案的时候再把数据拿出来拼合成答案就成了。这种操作一般都比较少，比如求答案只求一次，要不然也不能起到很好的优化效果。

要使用这种优化，状态的转移必须是连续的、整数域上的、递推式的

3 数据结构优化

除了可以对状态表示执行优化，我们还要考虑如何快速计算转移方程。

就比如你发现有的方程要你快速求前缀和、求区间和等等，那么可以尝试用树状数组线段树。

不过还有一种策略，就是直接把转移方程放到数据结构上来运行。这样也实现了快速找到决策的目的。

4 单调队列优化

4.1 一般的单调队列优化

单调队列，就是一种根据决策集合的单调性，及时排除无用的决策。

记得有个博客总结的很好：“假如有的选手比你小还比你强，那么你就可以退役了”。

这句看似调侃，实际上摆明了单调队列优化的核心逻辑，如果某个决策集合取值范围单调滑动（滑动窗口），决策点显然越“靠前”就可以存活更长时间，如果这样的点比靠后的节点更新还要优，那么靠后的决策就是没有用的，因为它已经不可能再取代靠前决策的地位。（无论从最优性还是合法性）

听起来不错，但是这里面有坑，你有的时候发现：你把还有用的决策踢出去了/下一个阶段你队列里的决策就不优了

这就是因为，你的这个问题可能并没有单调性，就是总结为书上最后那个1D/1D

简单来说，要能使用单调队列优化，你的状态转移方程需要满足：

• 决策集合取值范围两边变化单调性一致，要是一次函数（不一致就没必要用单调队列了，一个变量或者是一个不增加决策的队列都行）

• 中间转移求最值的那个多项式函数val要可以被分成只跟决策变量j有关和只跟状态变量i有关的

  我们这个优化是把决策过程省掉了，那么这样做要保证在状态变化的时候较优的决策仍然较优，那么如果含有ij交叉项，那么i变化的时候就不敢保证这一交叉项的值不会影响val的整体最优性。就比如减去了一个ij，那么val函数图像就会变成弯曲的，有的时候一移动i原来的大小关系就被打乱了

  例子：

  

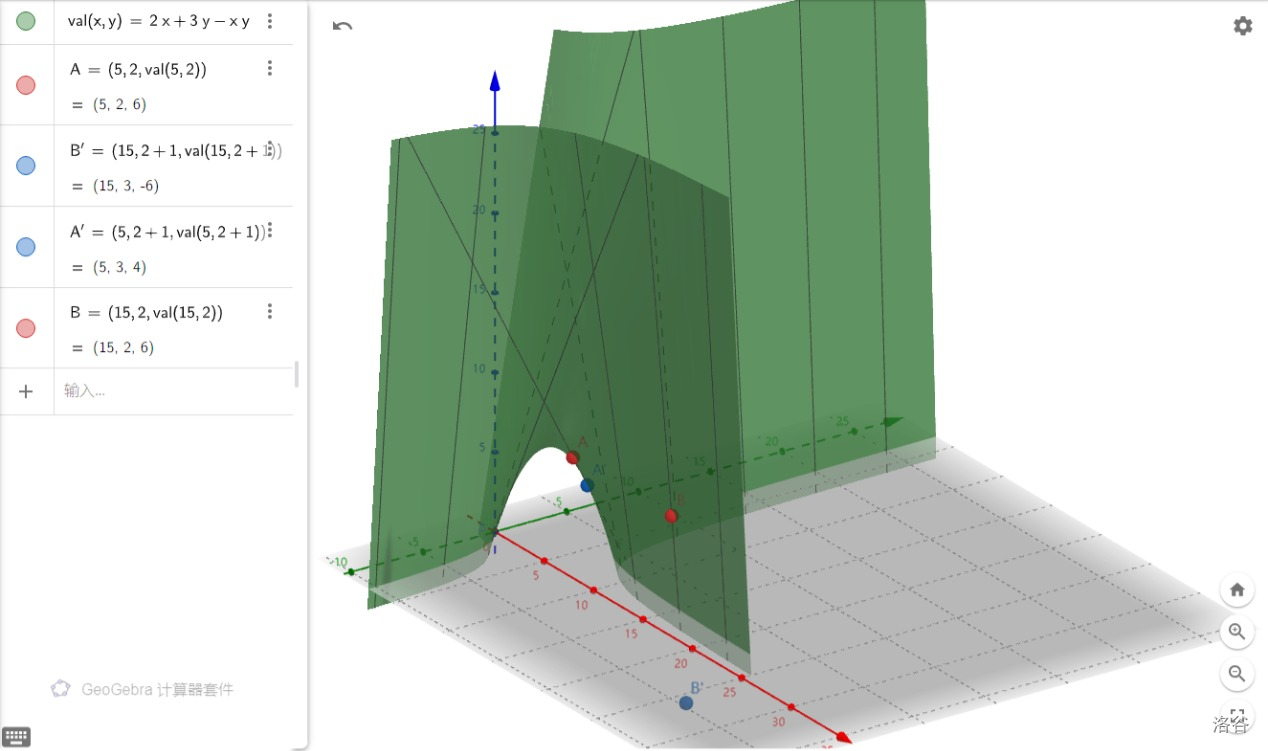
  图注：由图中A->A'，B->B’。（红色到蓝色）

4.2 单调队列优化多重背包

单调队列优化多重背包，就是将状态按除以Vi的余数分组，然后写出新的方程，然后按照方程执行计算。

这里主要说一下总结，那就是如果想要使用单调队列优化，不仅需要满足以上要求，还需要决策集合是高度重复的，然后每当状态改变时我们都要能够快速求到新的集合。

5 环形与后效性处理

5.1 环形处理

分为两种：

1. 进行两次DP，第二次强制从第一次漏掉的状态开始转移。

2. 破环成链法，复制一份接在末尾。使得每N个都对应原来的一种展开。

5.2 后效性处理

如果某一个问题有后效性，我们可以用高斯消元的方法直接求解转移方程。

通常这种题不会让你求最值的，因为有可能解出来inf，就跟SPFA遇上负环一样（本来就一样嘛）。多半求数学期望，也不可能求方案数，要不然也是inf，所以你可以去直接解它。