关于最短路
关于最短路
目录
- 最短路问题
- 概述
- 基本思路
- 性质
- BF暴搜
- DFS
- BFS
- 边权相同图
- Dijkstra
- 朴素的
- 过程
- 正确性
- 时间复杂度
- 堆优化
- 思路
- Bellman-Ford
- 朴素的
- 过程
- 原理
- SPFA:队列优化
- 过程
- 关于玄学:时间复杂度
- 变式:判断负环
- Floyd
- 过程
- 变式:传递闭包
- 变式:求路径最值的最值
- 变式:输出方案
- 存图的智慧
- 对比与总结
- 最短路简单应用
- 例一 [模版]负环
- 例二 Cow Party S - 堆优化dij
- 最短路变式应用
- 建图的智慧
- 例 path
- 总结
Part 1 最短路问题
1. 概述
最短路问题是在带权图上求两点之间最短距离的问题。
2. 基本思路
对于最短路问题,我们有很多算法可以解决问题,但是他们几乎都是基于两种思想:
- 选边连接成方案
- 选点连接成方案
而且,分析可知:
如果已知一个最短路序列\(A_1,A_2...A_n\),那么不论是选边还是选点,最短路序列\(A\)都可以由\(A_1,A_2...A_{n-1}\)之后再加上一条边构成方案,所以就可以使用DP,即floyd算法
3. 性质
-
对于边权为正的图,任意两个结点之间的最短路,不会经过重复的结点。
-
对于边权为正的图,任意两个结点之间的最短路,不会经过重复的边。
-
对于边权为正的图,任意两个结点之间的最短路,任意一条的结点数不会超过 n,边数不会超过 n-1。
Part 2 BF暴力搜索
1.DFS
简单的,dfs带回溯,每到达终点就更新答案。还有可以使用最优化优化。
2.BFS
其实不如就用spfa。
- 在边权相同图上
在边权相同图上,可以直接使用不取消标记的bfs
Part 3 Dijkstra
1.朴素的
- 过程
- 将与出发点直接相连的点进行扩展并确定他们距离原点的距离
- 选择已经扩展的点中距离原点最近的那个点A
- 确定与A直接相连的、未确定距离的点与原点的距离
- 重复2、3步,直到没有未确定距离的点
- 正确性
dij算法不可以在带有负边权的图上使用,否则会计算出较大的答案。
为什么呢?
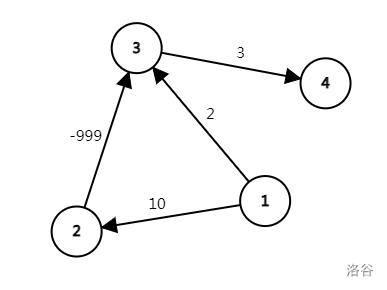
从上面过程可以看出,实际上dij基于贪心选点的方法扩展。这个贪心的正确性实际上是基于在正权图中,如果一条路径已经确定比最短路径大,那么之后他就不可能再成为最短路。什么意思呢,让我们来看图:
如果要求从\(1 \to 4\)的最短路,应该是哪一条呢?显然,是\(1 \to 2 \to 3 \to 4\)但是我们在第一步的时候,算法会贪心地认为,走3肯定比走2好,可是它不知道,后面有一条可以将距离缩小的负权边,所以会做出错误的决策。
代码:
// OI-wiki Version
struct edge {
int v, w;
};
vector<edge> e[maxn];
int dis[maxn], vis[maxn];
void dijkstra(int n, int s) {
memset(dis, 63, sizeof(dis));
dis[s] = 0;
for (int i = 1; i <= n; i++) {
int u = 0, mind = 0x3f3f3f3f;
for (int j = 1; j <= n; j++)
if (!vis[j] && dis[j] < mind) u = j, mind = dis[j];
vis[u] = true;
for (auto ed : e[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) dis[v] = dis[u] + w;
}
}
}
- 时间复杂度
可见,由于正权图上最短路性质3:节点数不超过n,排除原点的话,即每一次决定一个点,共n-1次。
其中,暴力作法需要每一次枚举所有点以寻找下一个点。
故该算法的朴素实现时间复杂度为\(O(n^2)\)
2.堆优化
- 思路
dij的堆优化就是将寻找下一个点的过程替换为堆来实现,从而将一个n变成log
但需要注意的是,由于实现原因,可能堆里会进入已经作为中心扩展过的点,所以需要手动排除他们
代码:
// C++ Version
struct edge {
int v, w;
};
struct node {
int dis, u;
bool operator>(const node& a) const { return dis > a.dis; }
};
vector<edge> e[maxn];
int dis[maxn], vis[maxn];
priority_queue<node, vector<node>, greater<node> > q;
void dijkstra(int n, int s) {
memset(dis, 63, sizeof(dis));
dis[s] = 0;
q.push({0, s});
while (!q.empty()) {
int u = q.top().u;
q.pop();
if (vis[u]) continue;
vis[u] = 1;
for (auto ed : e[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v], v});
}
}
}
}
Part 4 Bellman-Ford
1.朴素的
- 过程
Bellman-Ford 算法所做的,就是不断尝试对图上每一条边进行松弛。我们每进行一轮循环,就对图上所有的边都尝试进行一次松弛操作,当一次循环中没有成功的松弛操作时,算法停止。
- 原理
与dij不同,bellman-ford算法注重于边。我们可以思考,在每一次的松弛后,这张图发生了什么改变?
容易得出,如果一条边起点的最短距离是INF(未求出),那么对于这条边的松弛操作其实无效。因为INF+边长=INF。
所以我们抽离第一次松弛来看,就只有对原点相连的边的松弛操作有效(其实不一定,存边的顺序对此有影响,但是在最坏情况下,只有与原点相连的边的松弛操作有效)。推广到所有次数的松弛循环,应该只有对已经松弛成功的点的松弛有效。
所以每一次循环都至少会松弛一层,并多确定一条最短路上的边。故该算法的复杂度为\(O(nm)\)
2.SPFA:队列优化
- 过程
其实上,从我们刚刚的分析看出,有许多松弛其实是无效的,那么我们就只要松弛与当前相连的点即可。我们可以使用队列来实现。
代码:
// OI-wiki Version
struct edge {
int v, w;
};
vector<edge> e[maxn];
int dis[maxn], cnt[maxn], vis[maxn];
queue<int> q;
bool spfa(int n, int s) {
memset(dis, 63, sizeof(dis));
dis[s] = 0, vis[s] = 1;
q.push(s);
while (!q.empty()) {
int u = q.front();
q.pop(), vis[u] = 0;
for (auto ed : e[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
cnt[v] = cnt[u] + 1; // 记录最短路经过的边数
if (cnt[v] >= n) return false;
// 在不经过负环的情况下,最短路至多经过 n - 1 条边
// 因此如果经过了多于 n 条边,一定说明经过了负环
if (!vis[v]) q.push(v), vis[v] = 1;
}
}
}
return true;
}
- 玄学:时间复杂度
SPFA算法的理论最坏复杂度是\(O(nm)\),但他在随机图中表现较好。但是某些特殊构造的数据能欺骗spfa,从而浪费很多时间,例如菊花图、方格图。
为什么会被卡呢?
因为在spfa算法中,每一个点入队的次数是会随着图而变的,在某些图上,我们可以诱骗spfa多次更新无效点或者诱骗SPFA走入错误方向从而使得复杂度爆炸。
其实我们也有一些玄学的优化,例如:
除了队列优化(SPFA)之外,Bellman-Ford 还有其他形式的优化,这些优化在部分图上效果明显,但在某些特殊图上,最坏复杂度可能达到指数级。
堆优化:将队列换成堆,与 Dijkstra 的区别是允许一个点多次入队。在有负权边的图可能被卡成指数级复杂度。
栈优化:将队列换成栈(即将原来的 BFS 过程变成 DFS),在寻找负环时可能具有更高效率,但最坏时间复杂度仍然为指数级。
LLL 优化:将普通队列换成双端队列,每次将入队结点距离和队内距离平均值比较,如果更大则插入至队尾,否则插入队首。
SLF 优化:将普通队列换成双端队列,每次将入队结点距离和队首比较,如果更大则插入至队尾,否则插入队首。
D´Esopo-Pape 算法:将普通队列换成双端队列,如果一个节点之前没有入队,则将其插入队尾,否则插入队首。
- 变式:判断负环
但还有一种情况,如果从 原点出发,抵达一个负环时,松弛操作会无休止地进行下去。注意到前面的论证中已经说明了,对于最短路存在的图,松弛操作最多只会执行n-1 轮,因此如果第n轮循环时仍然存在能松弛的边,说明从原点出发,能够抵达一个负环。
注意
需要注意的是,以S为源点跑 Bellman-Ford 算法时,如果没有给出存在负环的结果,只能说明从S点出发不能抵达一个负环,而不能说明图上不存在负环。
因此如果需要判断整个图上是否存在负环,最严谨的做法是建立一个超级源点,向图上每个节点连一条权值为 0 的边,然后以超级源点为起点执行 Bellman-Ford 算法。
Part 5 Floyd
floyd是用来求任意两个结点之间的最短路的算法(全源最短路)。
复杂度比较高(\(O(n^3)\)),但是常数小,容易实现。
适用于任何图,不管有向无向,边权正负,但是最短路必须存在。(不能有个负环)
- 过程
我们设\(f_{i,j}\)是表示\(i \to j\)的最短路。考虑任意选择一个点\(k\)作为\(i \to j\)的中继节点,那么\(f_{i,j}={f_{i,k}+f_{k,j}}\)或者直接\(i \to j\),不借助中继节点。所以
\(\normalsize{f_{i,j}=min({f_{i,k}+f_{k,j},f_{i,j}})}\)
- 变式:传递闭包
传递闭包,指的是求任意两个点之间的连通性。整个过程就想把一个包从原点开始传递一样。只需要把方程改为:
\(\normalsize{f_{i,j}=({f_{i,k}\&\&f_{k,j})\text{\textbardbl}f_{i,j}}}\)
这样,如果可以\(i \to k\)且\(k \to j\)就说明\(i \to j\),或者可直接\(i \to j\)
- 变式:求路径最值的最值
只需要再把式子变成:\(\normalsize{f_{i,j}=min/max(max/min({f_{i,k},f_{k,j}),f_{i,j}})}\)
- 变式:输出方案
开一个 pre 数组,在更新距离的时候记录下来后面的点是如何转移过去的,算法结束前再递归地输出路径即可。
Floyd 要在转移时记录 pre[i][j] = k
Part 6 存图的智慧
通常,我们有三种存图方式:
- 邻接矩阵
设f[i][j]为\(i \to j\)的边长。
注意
- 初始化为INF
- \(i \to i\)即f[i][i]应设置为0
- 若有重边,要取最小的那一个
适用于朴素dij、floyd
- 邻接表(数组模拟链式前向星)
比较复杂,这里只给出代码,详见OI-wiki:
const int N=100000,M=100000;//n点数,m边数
int tot,head[N];
struct edge{
int v,w,to;
}e[M];
void add(int u,int v,int w){//添加边 u -> v 权为w的单向边
e[++tot]={v,w,head[u]};
head[u]=tot;
return;
}
//使用,遍历
for(int i=head[x];i;i=e[i].to){
...
}
很多算法都适用。特点是可以有针对性地遍历以x为起点的所有边。
- vector
开vector
优点同上。
Part 7 对比和总结
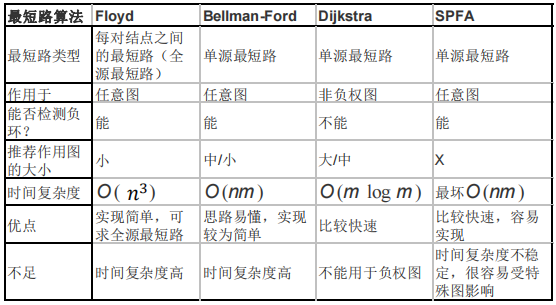
注:本表中Dijkstra是堆优化的
Part 8 最短路简单应用
-
例一 [模版]负环
都是比较模版化的题目,不做讲解。
Part 9 最短路变式应用
我们重点来看第三题。
Farmer John 最近为了扩张他的牛奶产业帝国而收购了一个新的农场。这一新的农场通过一个管道网络与附近的小镇相连,FJ 想要找出其中最合适的一组管道,将其购买并用来将牛奶从农场输送到小镇。
这个管道网络可以用 NN 个接合点(管道的端点)来描述,将其编号为$ 1 \ldots N1…N$。接合点 1 表示 FJ 的农场,接合点 N 表示小镇。有 M 条双向的管道,每条连接了两个接合点。使用第 ii 条管道需要 FJ 花费 c
i
美元购入,可以支持每秒 f
i
升牛奶的流量。
FJ 想要购买一条管道组成一条单一路径,路径的两端点分别为接合点 11 和 NN。这条路径的花费等于路径上所有管道的费用之和。路径上的流量等于路径上所有管道的最小流量(因为这是沿这条路径输送牛奶的瓶颈)。FJ 想要最大化路径流量与路径花费之比。保证存在从 11 到 NN之间的路径。
这道题中,路径的流量只取决于其流量最小的那条管道。
但是还有个问题。那就是FJ想让流量与花费之比最大。同时,我们还注意到fi的范围很小(原题中为1到1000正整数),因此我们可以枚举最小的fi,使最短路只经过大于fi的边来保证可以考虑所有情况。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,l;
bool vis[1005];
int dist[1005];
int sumf=0x3f3f3f3f;
double maxans=-0x3f3f3f3f;
struct edge {
int f,c;
int v;
};
vector<edge> mp[1005];
void ipt() {
cin>>n>>m;
int u,v,fi,ci;
for(int i=0; i<m; i++) {
cin>>u>>v>>ci>>fi;
mp[u].push_back((edge) {
fi,ci,v
});
mp[v].push_back((edge) {
fi,ci,u
});
l=max(l,fi);
}
}
void init() {
//sumc=0;
sumf=0x3f3f3f3f;
memset(dist,0x3f,sizeof(dist));
memset(vis,false,sizeof(vis));
dist[1]=0;
}
void update() {
if(dist[n]==0x3f3f3f3f) return;
maxans=max(maxans,(double)sumf/(double)dist[n]);
}
void spfa(int fi) {
queue<int> q;
q.push(1);
vis[1]=true;
while(!q.empty()) {
int ln=q.front();
q.pop();
vis[ln]=false;
for(int i=0; i<mp[ln].size(); i++) {
if(mp[ln][i].f>fi&&dist[ln]+mp[ln][i].c<dist[mp[ln][i].v]) {
dist[mp[ln][i].v]=dist[ln]+mp[ln][i].c;
if(!vis[mp[ln][i].v]) {
sumf=min(sumf,mp[ln][i].f);
q.push(mp[ln][i].v);
vis[mp[ln][i].v]=true;
}
}
}
}
}
int main() {
ipt();
for(int i=0; i<=l; i++) {
init();
spfa(i);
update();
}
cout<<floor(maxans*1000000);
}
Part 10 建图的智慧
- 例 path
给定长度为n的数列a,如果\(ai \& aj \neq 0\)(按位与),则在i,j之间存在一条长度为ai+aj的边,求1至所有点的最短路。
十分奇怪,对吧?最短路不难,主要是如何建图?
不难发现,如果两个数只要有一位都是1,那么他们之间就有一条边,并且该边边权是两个数之和,这样的描述让我们想到联系他们之间的共同点的归类思想。
因此我们可以建立一些虚点,例如(\(A_1,A_2...A_{30}\))。如果数x的第i位上是1,那么就将它和点\(A_i\)连一条边权为x的无向边。之后再跑SPFA。这样就使得我们把复杂的关系简单化到逐位,这样的思想很像并查集。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5,AI=35;
int n,head[N+AI],tot;
long long dist[N+AI];
struct edge{
int v,w,next;
}e[N*2*AI];
void add(int i,int j,int v){
e[++tot]={j,v,head[i]};
head[i]=tot;
}
bool vis[N+AI];
void spfa(int s){
memset(dist,0x3f,sizeof dist);
queue<int> q;
q.push(s);
dist[s]=0;
vis[s]=1;
while(!q.empty()){
int ln=q.front();q.pop();
vis[ln]=false;
for(int i=head[ln];i;i=e[i].next){
if(dist[ln]+e[i].w<dist[e[i].v]){
dist[e[i].v]=dist[ln]+e[i].w;
if(!vis[e[i].v]){
q.push(e[i].v);
vis[e[i].v]=true;
}
}
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
int x;cin>>x;
bitset<100> f;
f|=x;
for(int j=0;j<=34;j++){
if(f[j]){
add(i,j+n+1,x);
add(j+n+1,i,x);
}
}
}
spfa(1);
for(int i=1;i<=n;i++){
if(dist[i]==0x3f3f3f3f3f3f3f3f) cout<<"-1 ";
else cout<<dist[i]<<" ";
}
return 0;
}
Part 11 总结
总的来说,最短路问题是一个很有意思,并且重要的问题。他可以延伸出许多枝叶。相比之下,这些最短路算法虽然大多简单,但是要深刻理解其原理,才可将其推广应用,并可以体会到那算法中蕴含着的基本原理和营养以及前人熠熠生辉的智慧。
EOF
感谢观看。\(\Huge{QwQ}\)
本文来自博客园,作者:haozexu,转载请注明原文链接:https://www.cnblogs.com/haozexu/p/17488399.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号