向无法解开的明天伸手
《Untitled》
注:如果您是搜索标题来的,对不起,本文和标题没有关系,只是作者犯中二病了想取个不明所谓的标题。虽然这和我当时的心境有很大关系。
20250918
P4794 [BalticOI 2018] Alternating Current / 交流电
……都会变得,温暖,又明亮……
展开思考过程
Hinted 3/5 似乎没有性质,因此考虑做一步转化。 考虑一个点若被同种边通过大于 2 次,那么 必然有一次没有用,考虑每条边可以是区间 +1 或者是区间 -k(k 足够大),要求最终每个点 <0 并且绝对值不是 k 的倍数 让我想到同余最短路,但是我们可以考虑最长路, Hint:你知道吗,对于 b>=a,所以第一个 区间是必须选择的,然后有一种贪心策略…… 但是之后就不行了,因为不知道哪个区间是必须选择的。 称完全包含一个区间的区间叫这个被包含区间的祖先 一个区间如有一个以上祖先,那么就是没有用的, 称没有祖先的区间为顶级区间,有一个祖先的区间为次级区间 所以只保留顶层的区间和有一个祖先的区间, 有一个祖先的区间, 它一定与祖先选择的颜色是不同的。 我们还可发现一个性质,一个顶级区间里面,如果有次级区间, 他们一定是连在一起的,否则无解,因为不能有非次级区间的外部 区间前来补位,否则就一定有被覆盖 2 次的 次级区间 补丁:被两顶级区间覆盖的次级区间有用吗?应该也是 没有用,只要有解,通过调整方案应该总是可以完成。 那么我们可以把连在一起的次级区间(必须属于同一个顶级区间)合成一个 合并之后的次级区间也不可能有包含的情况 由于没有不能染色的地方, 所以顶级区间一定覆盖了整个轨道。 现在的情况就是一个大的带一个小的,然后 大的和小的一定分属两个轨道,我们令 F(i,0) 表示从 i 出发, 选择配色方案的哪一种,最远到哪里,然后执行记忆化搜索, 总之我们就是要找个环,现在每两个都不是完全覆盖的,我们 每个点拆成两个,然后连有向边,最后就是找环的问题。 我们 topo 排序解决即可,我们最终还需要解决 如何找到顶层区间的问题,考虑按左端点排序, 在 set 等设施内记录当前已经扫过的顶层区间右端点 唉唉还是不太靠谱,分开考虑,一个 set 存跨越了 n 的那些,一个 set 存遍历过的那些,然后走的时候记得把 这个好像可以倍长断环做,先不管,先 N^2 验证一下 注意我们认为如果两个区间一模一样的话,小标号的覆盖 大标号的。 好像不是很对。。。。。。。Key Trick: 先构造满足其中一个条件,同时保证另一个条件还可以满足。
神仙题目,关键思路是在保证另一颜色有区间可用的情况下确定其中一种颜色的区间,只要有一个点被覆盖两次,那么选择其中的一区间,另一区间给另一组就可以,但是有的时候,必须选择两条有交叉的区间,才能连起来,这个时候会消耗 2 个跨过某点的区间,所以需要中间交叉部分的点都有第三个可用区间的时候才能进行,显然一个点上如果有三个相同颜色的区间是不优的,不如留着给另一个颜色用。
解法就是判定问题,建边然后看有没有合法路径,但是断环之后可能会出现一个点上被选三个区间的情况,需要把其中不必要的区间删除。
Key observation: 类似记忆化搜索,递归搜索的过程中如果发现从 \(v\) 开始的递归过程与之前走过了什么无关,那么可以考虑优化。
注意到由于从 \(v\) 开始走的路径和从哪里出发的无关,如果搜索 \(x\) 的时候通过 \(v\) 不能到达 \(x+n\),那么分类讨论发现,也不能到达 \(y+n,\forall y>x\)。因此时间复杂度是线性的。
评价为四不像,下回再也不用 Hint 自动机了,精神分裂很严重。题解 K0stlin 等价于题解一。
- P11459 [USACO24DEC] It's Mooin' Time P - 洛谷 在花费 1.5h 后被丢掉了,原因是:闵可夫斯基和、凸优化
20250919
P9333 [JOIST 2023] 议会 / Council
这个题的处理方式好像很牛!本来一开题解,发现,完了,是 SOSDP 题,不会了,但是第一篇题解是一个类似折半搜索的做法,感觉很巧妙,不过原题解似乎写得不是很清楚。
本文将把二进制数视为一种特殊的集合。
首先转化成:有 \(N\) 个 \(M\) 位二进制数,构成可重集合 \(S\),还有 \(N\) 次询问,第 \(j\) 次询问给定一个 \(M\) 位二进制数 \(b_j\),那么答案可记作 \(\min_{i\in S} \left\{\lvert i\cup b_j\rvert\right\}\)。以下,我们令所有查询构成的可重集合位 \(Q=\{b_j\}\)。
在暴力算法下,我们需要对于所有 \((i\in S,j\in Q)\) 的二元组,计算 \(i\) 对 \(j\) 的贡献。这种算法是 \(O(n^2)=O(|S||Q|)\) 的。
但是,前 \(M/2\) 位相同的 \(i,j\in S\),对于后 \(M/2\) 位相同的 \(a,b\in Q\)(不妨认为 \(2\vert M\)),只要 \(i\) 对 \(a,b\) 的后 \(M/2\) 位比 \(j\) 优,那么由于他们前 \(M/2\) 位相同,\(i\) 就优于 \(j\)。因此,我们预处理 \(f_{i,j}\) 表示前 \(M/2\) 位为 \(i\) 的 \(a\in S\),后 \(M/2\) 位为 \(j\) 的 \(b\in Q\),\(a\) 对 \(b\) 的后 \(M/2\) 位的最小贡献,即可平衡预处理和查询的时间复杂度。
这种技巧,对于所有贡献按位独立的题目都适用,并且是在线的。
20250921
P5283 [十二省联考 2019] 异或粽子
展开思路
选择 k 个子区间,可有交,但是不能相同,求最大的区间异或和之和 换句话说,求异或和前 k 大的子区间,k<=2e5,a_i<=2^32-1求 k 次最大不就行了吗?求一次最大怎么办?
考虑前缀异或和做 Max Xor Pair 即可。
因此,考虑每一个位置结尾求出最大的 Max Xor Pair
然后,找出最大的,计入答案,然后考虑怎么求次大的,
这里理想情况下应该没有相同的前缀和,这个反正可以处理掉,先不管
所以问题就变成,求最大的,但是严格小于 val 的一个 Xor Pair,
这个并不难,依然使用原先的做 Max Xor Pair 的贪心即可。
似乎有点问题,还是得维护一下子树内还有没有可用的数,
但是其实我们只需要找到 val 的最后一个可以选择变成 0 的 1
即可,也就是第一个与 val 的方案取儿子不同的位置,
原先选择的那子树现在一定不会选择了。
那么我们此时使用一个可持久化 01Trie 即可完成
看题解,resolved using 15min
前 \(k\) 大可以考虑选择最大的,然后求出次大尝试更新答案。
Trie 树可以求次大的。
P5280 [ZJOI2019] 线段树
对于较多的点是不能维护复杂标记的,本题需要将与时间有关的转移放到那些可以暴力的点上。
P8339 [AHOI2022] 钥匙
静态的询问。。
直接考虑倍增维护区间内钥匙数、箱子数、箱子匹配完
钥匙之后还有多少钥匙/箱子,随便做做就完了。
不对,肯定不对,k<=5 根本没用到。
哦这不是还有颜色吗。。。。
我们考虑就近匹配钥匙和箱子, 肯定是对的,
所以就是两个方向,一个是钥匙向上匹配最近箱子,
一个是箱子往上匹配最近钥匙,然后穿过 LCA 的
可以考虑能否直接计算。
不过说实话,即使是这样,也没有用到 k<=5
所以我们必须考虑,其实应该对每一个箱子,都匹上
最靠近的钥匙,也就是在不经过钥匙的情况下,能达到的所有钥匙
还需要修正
如果一个钥匙和一个箱子,中间的连线上面有另外没匹配钥匙,
那么就不能连上,否则就连上,这样就行了。我们考虑这个具体有多少对。
还不是很清楚。
应该说,从钥匙走到箱子,中间做一个类似栈的东西。
那么我们考虑这样走一次至多连接 5 条边,从
每个点开始可以向另外的所有点走,所以一个钥匙可以有 5n 个贡献?
不对的, 就算每个点都和同色点连边,那么也只有 5col 个边。
这样匹配数是 O(N)
然后匹配的时候,我们只会从每个钥匙开始走,然后只会遍历同色点。
这样没什么问题。不过每次都建虚树,挺麻烦。
然后我们要求解的就是路径上有多少匹配
考虑匹配对于可能贡献的查询是一个矩形,
本质上我们求一个点被多少矩形覆盖,这个容易扫描线。
看下题解,看看怎么方便建边 好吧题解就是虚树。
20250922
-
T2:容斥往往用一个好算的限制替换难算的限制,但是如果容斥维度过多,可能导致反而难算。
-
T4:注意题目中求 f(ij) 的时候,注意下 f 是不是积性函数。中间几步技巧性很强,下次也不一定能做。但是转化条件为 \([h(x)=1]\) 然后用莫比乌斯反演将判定转为计算,这个很有用。
P10681 [COTS 2024] 奇偶矩阵 Tablica
这个没做出来,关键是最开始转化没有想到,确定和之后,把每一列的 1 去决策放在哪行里面,就转化成我们喜欢的集合分划的问题,然后后面容斥是容易的。这种题大部分开始的时候都需要转化,直接尝试容斥往往是 naive 的。
dpsk 还是和人类助教有很大差别,它根本不懂什么地方是很关键的。
20250923
-
T2,最开始读错题了浪费 1h。然后没有想到它 DP 的转移是 n 个 n 个一组的,或者说根本就没有用 DP 的角度看。
-
T3,这个题还是很可做的,应该说 DP 套 DP 的做法是很清楚的,论细节恐怕 T2 更胜一筹。这种生成一个排列的题目,一般都都有尾插和按其他顺序的思路,因为需要考虑哪些已经有了,一般都不是直接尾插,而是从小到大,或者尾插之后考虑相对位置的移动。
P12768 [POI 2018 R3] 三人编程锦标赛 Triinformathlon
其实主席树建图是真的可以做吧。。。。但是会被卡空间。
Key Trick (竞赛图) 竞赛图的 SCC 之间满足严格全序。
使用 std::sort 或者 std::stable_sort 按照竞赛图的边排序,SCC 就会缩成一个区间,然后缩点,相当于对竞赛图做了传递闭包。
20250924
P11973 [JOI Open 2020] 黑白点 Monochrome Points
我们设区间的 len 是中间有多少数,也就是 r-l-1
我们可以发现,这个是 min(n-1,len,2n-2-len)
len=2n-2-len => len=n-1
那么,最优方案中是不是让选定的所有区间都是达到自己最大呢?
或者说,我们的目标是不是就和这个区间长度有什么关系?
答案,会不会就是最大化 sum(min(len,2n-2-len))/2 呢?
这个有什么道理吗? 我们写个暴力来匹配下
似乎没有问题,感觉挺对,但是似乎挺难说清楚,如果我现在在考试
那么我大概不会深究这个问题。
那么好,看上去像是最大权完美匹配。不过是特殊的图。
这个是一个折了一下的一次函数,
考虑任意 n 个之内,没有两个相离的区间。
神题。感觉目前题解证明这个结论并不完整,其实不能说明这样构造取得的就是答案,虽然直观上很对。目前题解是这样的逻辑:猜测 \(A\) 问题的解是原问题答案,\(A\) 问题等价于 \(B\) 问题,所以现在我们发现构造 \(C\) 能够得到 \(B\) 问题的答案,因此构造 \(C\) 得出了答案。但是其实偷换了一个概念,构造 \(C\) 确实得出了问题 \(B\) 的答案,进而,得出了问题 \(A\) 的答案,但是并不清楚是否得出了原问题的答案。
将黑白点均匀摆到环上,下称“边”为相邻两个点之间的线段,令其长度为 \(1\)。
Key observation: 问题的答案二倍是最大化每对匹配的环上距离之和。
这个可以直接猜,这里我是有人提示让我考虑一个匹配最多交多少匹配我才发现的。
Trick: 发现环上距离是两个距离取 \(\min\),但是外面又要取 \(\max\),方向不统一,考虑一对点 \((a,b)\),他们的环上距离等于环长减去 \((c,b)\) 的环上距离,其中 \(c\) 为 \(a\) 以圆心为对称中心进行中心对称之后的位置。
此时我们可以转化为取 \(\min\)。
Key observation: 最优方案是,分别从某个位置开始顺时针把白点和黑点排成一列,对应匹配。
\(\implies\) 环上至少有一条边不会被经过。
Trick: 断环,考虑把计算距离变成计算每条边被贡献到答案多少次,那么一个边被贡献的次数即为其前面(注意此时已经断环)黑点和白点数量差。因此我们考虑黑点设为 \(1\),白点设为 \(-1\),计算前缀和。
Trick: 循环移位原数组 \(k\) 轮,考虑前缀和数组的变化。
P11432 [COCI 2024/2025 #2] 流明 Blistavost
只能说我是急急国王,所以看了题解。但是其实这个是经典模型了,乱猜贪心是很没前途的。
20250925
我好像突然搞懂了一点,很多时候你看一个题目,如果实在找不出来性质,那么可能说明你的”语言“不够优秀,也就是说你如何表示这个题目和其中的对象很关键。
别急。比赛还有这么久,急什么。继续手玩,发现如果 i 把 j 杀掉了就 i→j 连一条边,最后的形态是若干条以某个点为中心,两端连向中间的链。对其 DP 就可以做到 O(n3)!然后实现起来有不少细节,不过这么点细节根本没什么难度——成功实现了 O(n3) 的代码。只需要一个前缀和和一个 ST 表就可以轻松优化到 O(n2),过了。
如果你不进行这样一个操作,那么你很难去思考操作背后,到底不同操作之间有什么联系。也就是说,换种语言,原本不会考虑的方向,现在就有了。
以上的思考仅适用于大部分需要找性质的场景。其实代数式也是语言,不是吗。
P5324 [BJOI2019] 删数
这道题,我一直的思考点就是在拿着一个序列,然后左右移动中间的分割线,但是这个操作不仅很复杂,不容易找到最优策略,而且限制了我能做的操作,相当于隐形施加了一个额外限制:我必须把其前驱或后继改成它,况且最后即使找到,大概率也是求一个线段面积并一类的东西,这个很不好求,所以这是一种很差的语言。
但是我很难意识到这一点,经常卡住很多时候就是因为我不知道找不出性质是因为我的表示方法不够好,而还是一直在死磕。
因此我们此题应该采用更优秀的表示方法,结合数的大小和个数两个限制,我们拿一个数 \(x\),把他排在它本应该在的区间。在这种表示下,有重叠和空位都是非法的,那么很容易知道修正的方法就是把重叠的拿去填空——由于恰有 \(n\) 个数 \(n\) 个位置,所以如果有错配的现象发生(即重叠),一定意味着有数的浪费,一定另一处有一个空位置,那么我们就发现了本题的性质,显然需要修正空位置的个数次。
P5371 [SNOI2019] 纸牌
太简单,不说了。注意搞清楚题意。
P7115 [NOIP2020] 移球游戏
比较的神秘,但是这种题的通用做法就是,你需要找出一个好用的基础操作,本题中你可以通过玩 Subtask 1 玩出来。然后其实这个时候分数就很不错了,而且,通过先构造 0 序列来卡常,还能通过。正解是一个分治并模拟排序的过程,因为本身这种基础操作就是在排序。
20250927
P5303 [GXOI/GZOI2019] 逼死强迫症
太简单。
P5306 [COCI 2018/2019 #5] Transport
太简单。
20250928
40/70 183/400; Expected 23/70; 253/400
-
T1:数组开小 -40
-
T2:细节错误 -30
本题是之前在云斗 OJ 做过的原题。但是题解说明,其实这个题可以 \(O(n+q)\) 做,其实和 \(O((n+q)\log n)\) 的核心思路一致,但是维护的时候考虑用 DFS 差量法来求解。
-
T3:其实本题不难,核心就是要注意到最后 5 位之外的位,都只可能有一次进位,其实没有发现,就是一个视角的问题,当时为了打 40pts 的暴力,我把问题抽象成维护进位数组,但是如果你回到最原始的意义,也就是第 \(i\) 行等于第一行加 \(i-1\),那么最多加 \(n\),所以有变化的最多就是最后 \(\log_{10}n\) 位,其余位置变化只可能有一处,就是后 \(\log_{10}n=5\) 位如果有 \(99999\to 00000\),那么前面就会多出这一次进位。所以最后先用最后几位的数字来限制 \(99999\) 的位置,再用其他位的非数字来限制,最后随便取一个就是答案。
但是实现起来并不简单
(実装がかなり大変です)。
P11665 [JOI 2025 Final] 只不过是长的领带 2 / Just Long Neckties 2
当前的选择方案必须得捆成一个状态才行,因为内外执行的是不一样的最优化
符号,也就是说你不能把每一种长度的拆开最优化,因为
你从上一个位置转移,那个位置的方案可能跟你当前这个是不一样的,
犯了一个很严重的错误,其实凭感觉设出来 DP 是不行的,最后求出来的并不是你想要的,最后求出来的只是说明存在一个序列存在这么长的 LDS,对求答案是没有帮助的。所以必须保证你的是 \(f_{i,x}\) 表示选了 \(i\),并且 LDS 就是 \(x\) 是否可能。
但是这个是不能转移的,因为你肯定不能只记录长度,一般求 LDS 是不需要记录序列的,但是这个题目,有点像 DP 套 DP,它里面这个 LDS 的转移是需要知道外面选了什么数的……吗?真的需要记录所有数吗?其实我们只需要记录不同长度的下降序列中,结尾最大的那个即可,容易观察到,长度为 \(i\) 的下降序列的前缀可以当作长度 \(j<i\) 的下降序列,因此所有这些结尾是单调且不重的,我们可以把它们压到一个二进制数里面,一个数后面有多少 1,就意味着它是长度为几的下降序列的最大结尾。更新和转移是容易的。
但是这样还是不能通过,考虑把可行性 DP 的其中一个维度转化成值。我们发现,一个状态 \(S\)(即一个结尾的方案),我们只关心它最远能够适用到哪里,也就是最大的 \(i\) 使得 \(f_{i,S}\) 是 1。我们可以求这个并转移。
20250929
这次模拟赛集中体现了一个问题,就是拿到一道题之后,我最开始会盲目的进行一些分析,而这些分析很大程度上限制了我之后的思考,如果它们是不对的,可能导致付出很大的代价。
-
T1:1.5h,写了 3k,\(O(n\log n)\),最后因为空间开大了 MLE(这一点是技术无关的,很可能是最开始范围看错了)。但是完全没有这么复杂的!我们只需要考虑一个点能否加入前面已经存在的一个块即可,也就是说,我们考虑是否存在当前点与之前某点连向对面同一点,此时就完全只需要解决边的存在性问题,我发现的支配性质就可以适用,而且不再需要树状数组。
我做得复杂,是因为我一开始将这个支配性质用于单调栈,然后认为只要不断合并连边的区间就可以了,但是这个做法后来证明是错误的,而且并不是很难看出的错误,完全是因为我没有认真检查导致的,我为它打了补丁之后还是必须求解边的存在性问题,但是由于是基于这个做法上加入的新逻辑,所以它复杂而且有其他限制使我需要数据结构。
-
T2:
鬼题,N<=500,数据保证 fa_i<i 与其转期望拆贡献,不如试试里层的组合意义。 组合意义是,每次从相邻两条路径的重合部分取一个点, 有多少方案。 转化,选出 n 个点(可以重复),使得相邻两个点在它子树里面。 考虑反向计数,转化成计数选点的方案对应多少合法排列。 那么一个排列中点需要在左右两个方案中点的子树交里面。 这意味着相邻这两个方案中点必须是祖先后代关系的。 祖先后代关系不是一种等价关系。 转化为每次你只能朝上或者朝下走(可以不走),然后到达一个新 的方案中点。现在考虑排列计数的问题, 这种问题我们往往采用连续段 DP,当然其实这里 倒是没什么特别大的关系,我们逐步确定倒数两个方案中点的时候, 其实相邻两排列点之间的限制已经被解耦了。 所以现在就只是限制这个新排列点必须在某个子树内取, 也就是说,考虑 dfn 的话在一个区间内。 nm,15 分。 考虑单求一个方案怎么求。 stop 考虑一个树形 DP,因为单求一个方案并不是困难的, 只需要将子树内已选的减去不考虑即可, 所以我们考虑 f_{x,y,k,0/1} 表示完全考虑了 x 子树内所有点 充当方案点之后,方案中还有 y 个空位置,已选的构成 k 连续段, 是否已经锁定了最左边和最右边, 此时,可能的排列数有多少个。 考虑转移,显然,来自不同子树的连续段不能直接拼接为一个。 如果锁左边/右边了,那么之后分配的时候就要注意必须让它当最左边 (显然不可以有两个子树同时锁左/右边,要不然我分配给谁??) 然后现在就是考虑用多少 x,我们遵守锁定规则排好之后, 考虑插入若干 x,考虑分配到每个间隔,然后再决策插完之后 每个 x 是否要和左边第一个东西合成一段 (注意不要同时决策右边,让右边的东西来决策,还要注意如果插在了最左边, 第一个不能决策) 然后考虑更新 f 值怎么更新,如果决定锁左边/右边,若为 x, 那么就相当于确认第一个数要在 x 之内,设当前区间内已决定 g 个排列点, (这个显然可以用空位数量、段数量和是否锁左右来计算), 那么就是乘以 (siz_x-g) 这个插入机制可能要改改 然后考虑新决策形成的段内,我如果插入在 某一段的右边,那么显然这个位置就新贡献了一个那一段右边的子树点, 这个也就是说对于每一段我们都要假定已经有了右边的一个,所以要算进去。 哎呀反正能转移,但是这么麻烦,估计流程需要优化, 你这状态数都是很大的,你转移难道还能是 O(1) 的??? 其实也不一定是很高的,因为这个其实是树形背包呢。 但总之我应该肯定是写不出来了。。。。。。 就是写出来了,30 分,你给谁拿? zh我最开始就做了很多转化,但是事实上,最后还是需要依靠连续段 DP,而且非常复杂不可写,也没法优化。但是至少从这个题我知道了,排列计数的题,如果有关于排列相邻两项的转移,那么连续段 DP 是可以尝试的。直接做连续段 DP 就简单多了,根本不需要任何转化。
-
T3:啊,这个怎么做?
关键是和一般数颜色一样,考虑关心子树内深度最小的某个颜色的点。那么我们维护每个点的最小深度,显然直接合并时不行的,考虑 dsu on tree 即可。由于还要在线,直接用 dsu on tree 加主席树维护可持久化的最浅深度计数数组,然后我们还有 \(O(nq)\) 个额外询问,询问一个颜色 \(c\) 在 \(x\) 子树内的最小深度。但是这个其实是可以离线做的,直接在 dsu on tree 之前处理出每个点有需要问哪些颜色即可。
-
T4:其实是一个非常“传统”的一个冒泡排序性质题。我这么说是因为冒泡排序的分析方法就那么几个,这个题就是其中一个,分析起来并不复杂,也就是冒泡排序那几个老性质,上次 20250404 的那个甚至非常不常见,最关键的一点是你要考虑把数按照大小差别染色,如果不这么考虑可能很难想出来。然后式子优化起来也很简单。
20250930
43/70 ideal 18/70 | 12/70; 100 -> 230/250
-
T1:比较简单
-
T2:写得很复杂,最后没调出来,赛后 9 分钟过了。这个题你要直接猜怎么构造可能也不是不行,但是假如你把曼哈顿坐标系转换成切比雪夫坐标系,那么就可以看作是两个坐标可以独立选择正负 1,那么构造方案就很好想了,也不用写很复杂的 DP。大概是经典的 Trick,切比雪夫距离下两个维度是分开的,可能更好处理。
-
T3:先考虑不删点,怎么求全局 LIS,显然需要用两个子树内的 LDS LIS 拼起来。考虑拼接这个操作肯定是 \(O(siz)\) 的,所以考虑 DSU ON TREE(标程的单 \(\log\) 方法只是这里有优化)。然后我们考虑直接枚举删哪个点,需要知道枚举的那个点为根,其他子树里面的 LIS,对于每个根都求显然不现实,但是显然删点必须删最开始的 LIS 上的一个点,因此只需要枚举一条链上的,那么求一条链周围的子树,可在链两头分别做上述 DSU ON TREE。
这个单 \(\log\) 的优化是长链剖分,但是我们需要考虑 LIS 的另一种解法,也就是在 P11665 Just long necktie 中提到的:
-
LIS 求法一:记录结尾为 \(i\) 的最长序列有多长
-
LIS 求法二:记录长度为 \(i\) 的序列最小结尾是多少
我们需要求法二,因为这样,前者记录的个数与子树大小(实际上是颜色数)有关,后者记录的个数与子树深度有关。如果一个 DP 的有效状态数和树的深度有关,那么考虑长链剖分,其实类似 DSU ON TREE,只不过,这一次,是从“长儿子”继承,从“短儿子”暴力加入。总共加入次数 \(O(n)\),但是单次加入需要维护当前最长 LIS,一次\(O(\log n)\) 。
-
20251001
rk7 / worst 22
-
T1:写了一个错误的做法,场上没有发现复杂度是错的,但是通过了。主要思路是正确的。最开始,我考虑顺序转移的时候没有认真考虑转移条件,认为通过前缀和取出一段不可行,但是其实是可以的,这一点没有留下记录。然后后来我回溯之后直接放弃了顺序转移。然后涉及到没有逆元的问题,这种问题的通用处理方式就是把 \(\gcd\) 除掉,这个我也用到了,但是我是直接解方程,没有利用所有可转移区间都是有公共后缀的。
关键 Trick 是,考虑把 \(D\) 提出来,若 \(2^a5^b\vert D\),一个数能否被 \(2^a5^b\) 整除只和后面 \(\max\{a,b\}\) 位有关(可以推广到其他进制),暴力处理这些位置,然后转化为求前面能整除 \(D/2^a5^b\) 的,此时模数于 \(10\) 互质,可以求逆元。
-
T2:太简单
-
T3:转移式是很简单的,但是我没有考虑去把他拆掉,使得我必须用 DDP,这就很麻烦了。
本题也可以先考虑用期望线性性拆开成若干轮从 1 开始走,只需要知道一轮内走到终点的概率、回到根的期望步数。前者等于终点到根的点出度逆元之积。后者再次考虑线性性,拆为边的贡献,每次修改考虑区间乘。类似扫描线矩形面积并,我们要排除一个区间的贡献时,给他上面记录一个被删的次数即可。这样写起来还更简单些,否则你需要像 std 一样还得考虑维护每个叶子哦。
Tips: 扫描线矩形面积并线段树标记的正确性依赖于它删除和加入是配对的。
即使这样,仍然有点难写。
20251002
P10789 [NOI2024] 登山
“为什么要攀登?因为山就在那里。”
考虑如果按照 DFS 顺序转移,那么可以用差分法+区间加单点查来求出子树内
的合法折返点。
我们如果想要进一步优化,其实就是对,
维护的这个线段树上,把这一段提取出来,然后
做区间乘法之后合并到某一个累加线段树上,
这个累加线段树一直上传(做子树累加线段树合并),
然后就能拿到 F 了。
但是这个应该已经属于爆改数据结构的范畴了,这个肯定不是线段树分裂合并
能够支持的。
[CHOICE A->B] 我们考虑是继续优化这个操作,还是去用其他手段优化 DP。
[B.I] 欸,这个问题是不是等于区间乘法带历史和来着?不是很一样
总之:有序列 A,B
A 维护区间加 1
B 维护将对应位置 A*k 加到 B 上。
我觉得这个不可能完成。
不可能吗?这个标记,好像是可以下放的吗?
似乎并非如此解决的?再想想,不行,这样会导致需要递归下放标记。
我觉得应该放弃。[DEPRECATE]
[B.II] 我们考虑从折返点的角度优化 DP。
整理下,我们如果求出转移点要求都相同的
嗯,我觉得,如果要实现复杂度的优化,那么刷表法转移,
你必然要考虑两个实体,我希望先考虑一下填表法 [TRACE][BREAK]
填表法,其实本质还是差不多。
现在从 i -> j 的限制还主要是,
i 的深度限制,中间点的子树限制,中间点的跳跃距离限制。
好像还得求出所有起点的?这样看来,反着 DP 更对一些。
那么现在我们要维护的东西是,A 和 B,B 决定了 A 要贡献
几次,我们现在对 B 区间加,A 单修,然后区间查询 A*B。
怎么题解似乎没有 [TRACE]
[TRACE]
所以这玩意能优化吗??????
我们考虑抛弃 DP,我们发现,在确定起点的情况下
其实是容易根据折返点等确定冲刺点的,我们考虑这一点。
因为若 x 是折返点,那么上一个冲刺点显然容易求出,即
第一个 x 的祖先且为起点祖先的,或说 LCA
考虑枚举第一个冲刺的折返点并继承答案,
这样相对可控,那么我们考虑是否可以直接就折返点
来贡献到起点。什么,这就是 DP。
[SUDO HINT] 等一下!!!!
我搞错了!!!!下滑到子树内某个结点中途是要算 limit 的!!
这下性质就完全不同了。
现在再考虑 h=0
此时相当于先让每个点加上 cnt_x*sum_till_x (指的是从 1-x 上的 f 前缀和)
然后再链减去 1-L 的那些,然后再将不该加的 sum_till_x 减掉,
然后在加上该加的 1-R 那些。
然后,如果 h!=0,但是 min_v 还是单调的,
这能搞个毛啊!!!
试试 l=r
这个也成,因为段数少就能做。
最致命的问题是,我没有搞清楚题意!我最开始忘了要对于每一个开头求,然后我在简化题意的时候又出了问题,没有意识到往下走的路上也是有限制的,所以我最开始说题解怎么没有那个地方 [Trace],我得到的做法在我这个题意里面是对的,其实题解里面也有类似的,但是由于我搞错了题意,也就只有一点类似了。
20251008
P11831 [省选联考 2025] 追忆
我常常追忆过去
补掉了 recall。最大的问题是思路的僵化,若干种条件,如果看作是满足若干条件的集合的合并,那么就做完一半了,如果坚持在每个点上维护满足这个点能到的点,永远也做不出来。然后由于 bitset 操作没办法做到和块长同阶,所以必须只能做 \(O(1)\) 次 bitset 操作,所以对于这个区间限制,显然是可差分的,考虑分块的时候按后缀分块,即可解决。
20251009
P8338 [AHOI2022] 排列
疑似太简单了点。
P8316 [CQOI2016] 伪光滑数
多路归并的 Trick,如果在一个巨大的状态空间内求第 \(k\) 极值,但是 \(k\) 不会很大,那么我们只需要找到一种有序、不重不漏遍历状态空间的方式,同时为了保证复杂度,还需要保证每个状态的后继状态较少(类似子问题重叠)。
P7916 [CSP-S 2021] 交通规划
基本对了,但是这个必须用区间 DP 来解决似乎
但是为什么不能从同色节点之间穿出去?
破案了,可以,但是我们可以转化为这条路径是绕出边界
再绕回来的类型
也就是说
边界--------------------
| |
这里有两个黑点,那么路径可能是
---------+ +-----+
| | |
| | |
边界-----------------------
| +-------+ |
这种。给俩同色点之间连上虚点即可。所以就解决了刚才的那种情况。。。
那么问题现在就变成环上等量异色点完美匹配,最优
情况下存在一个不交叉的完美匹配,能通过区间 DP 解决。
总之还是抓好对偶图这个关键比较好考虑。
确实感觉比上次用 CSP-S 2021 全真模拟的时候强得多,这次能想到 80~90% 了,但是最后一步没有完成。
20251010
P3974 [TJOI2015] 组合数学
太简单了
P10231 [COCI 2023/2024 #4] Putovanje
很奇怪一个题,我直接用暴力艹过去了。但是正解是这样的:
如果只有一个限制,那么我们最好从这个点开始跑最短路,找出所有正确的终点即可。但是如果有多个限制,考虑把边权变成 \(-1\) 做多源最长路,最后取最长路为 \(0\) 的,但是通过这个算法我们只能知道某一个点可能满足其中某些点的限制,但是不一定符合所有关键点的要求,有可能在原图上距离某些点太远了(太近的情况,会导致多源最长路大于 \(0\),可以被筛掉)。但是可以发现,满足所有限制的能被所有关键点更新最长路(相等也算更新)。因此维护一个 bitset 表示当前结点能被哪些起点更新最长路径。
感觉要想到这一点挺不容易的——你可能会忽略掉多源最长路,如果你想了这样一个“错误”算法,反而可能得到正解。
P7221 [JSOI2010] 蔬菜庆典
我们只要尽量构造这种情况即可,最开始的时候,
一个点的所有儿子一定权值全是相等的
所以就是看这种情况 vi != vp+vc-vi
只要 2vi!=vp+vc 这种情况且 vi 存在兄弟,
那么就可以构造出来了,我们考虑
vp+vc-vi
vpp+vp+vc-vi-vp
vppp+vc-vi
考虑对于一条链,依次
VI vp+vc-vi
VP vpp+vp+vc-vi-vp = vpp+vc-vi
VI vpp+vc-vi+vc-vp-vc+vi = vpp + vc - vp
VP vpp-vp+vi = vpp+vi-vp
VI vi
VP vp
对于一条链的操作还挺复杂的。
也就是说反复对链上两个点操作会使得他们变回去
BACKTR
所以对于没有 INF 的情况,最大的时候,
一定还是满足所有儿子都相同,并且这个时候
通过所有操作都
我们发现这个操作其实可以变成加上父亲和任何一个子树内的点然后减去
最后还是被绕进去了,这种奇怪的操作必须考虑什么东西是保证不变的。一定不能递归地去想。
其实考虑链上的复杂操作是没意义的,因为只要变了就不行,只需要考虑变没变,不需要考虑变了多少。
如果一个点是多叉的而且不是 INF,那么它每一个后代的权值都不能改变,一旦改变就是 INF,也即都要满足上面得到的 \(2v_i=v_p+v_c\)。
还有一点,从根到分叉点这段路径上点如果变化了,那么可以导致下面的某儿子变化,因此这些点都不能改变。
考虑从根把根的儿子当成若干子问题,如果某个子问题是这种有分叉的,那么这个子问题所有点应该完全不能动才对。否则如果是一条链,那么它是可以动的。
考虑经典 Trick,原操作等价于交换差分数组的相邻两项,排序即可 。
P7962 [NOIP2021] 方差
鬼!这个玩意怎么 TM 看出来是单谷的???
考场上还是记得打暴力打表吧,这个东西打表不太可能看不出来,尤其是你已经知道要做差分之后。剩余部分比较简单。
20251011
P6718 [CCO 2018] Flop Sorting
主要是没有想到合并的时候还可以再套一个按值域分治。
CMD,这个是怎么想到的??????
我当然知道合并的时候如果值域不交那么是容易的,
虽然你可以认为这个是 Trick,但是首先必须明确的方向就是:
肯定是排序算法,肯定不是快排,每次基础操作必须是线性,
做的次数必须是 log^k,不能是 poly,这个方向是可能性最大的。
本题的关键是我们要有意识的发现我们能够快速解决的是原问题的一个特殊子问题,因此可尝试将问题划分为这种子问题,分治是常见的手段。
20251013
P11119 [ROI 2024] 保持连接 (Day 2)
最开始想麻烦了,而且还是错误的,因为最开始的转化就是错误的,我觉得我做了一个惊天地泣鬼神的转化,可惜是错的。正解其实超级简单,就是基于 \(O(N^2)\) 的暴力 DP,然后直接计算将某位置更换为备用天线对转移造成的影响。
CF1578B Building Forest Trails
哎呀不想想了,有点脑雾,感觉燃尽了,遂 ctj。
这个题很怪异,要对一对脑电波,最关键的点是要刻画与某条边有交的连通块的特征,但是如果你没有画成题解那样的话,可能确实是不容易发现的。也就是要用合适的方法描述连通块之间不交这个条件,在这种表示方法的基础上看如何一个一个遍历与修改边相交的边就比较容易了。
有时间来实现这两个
20251014
If No FST 286
-
T1
考虑确定一个唯一顺序,防止对于本质相同方案的重复计算。
-
T2
注意到可以将斐波那契数列的项换成其矩阵表示,这样就能够拆项了,否则不可能 DP。
-
T3
不知道啥玩意。分块打表 70pts 跑路。
事实证明,一直去找 \(x+\operatorname{popcount}(x)\) 的性质是不明智的——它根本没有性质,更不可能存在通项公式,解决此问题的唯一方式就是二分/倍增。
本操作只有一个性质,即 \(\operatorname{popcount}\) 的值小于 \(\log n\),所以对于最低 \(\log\log n\) 位,它们的变化是比较频繁的,而对于更高位,唯一的变化就是有时会进 \(1\) 到这些高位,我们接下来称前者为低位,后者为高位。
如果我们考虑用倍增,就得计算一个数往后跳 \(2^i\)(即 \(x\to x+2^i\))需要几时刻,那么我们发现这个本质就是求,需要多少步,从初值为 \(x\) 开始变成 \(x+2^i\),但是这有可能是不能做到的,因为不可避免地,我们发现最低 \(\log\log n\) 位也会跟着变,这是我们没法控制的,这也就是为什么有的数不能被这种操作得到。那么应该分开看,我们现在有必要求出 \(f_{i,j},g_{i,j}\) 表示 \(i\to i+2^j\) 这个过程中 \(i\) 的后面几位变成什么了、花费多少时间。
那这个过程中 \(i\) 只影响了每次的 \(\operatorname{popcount}\)。我们可以将数按照高位的 \(\operatorname{popcount}\) 和低位的值分成 \(\log^2 n\) 类,这些类别 \(+2^i\) 之后的转移都是一样的,可以放在一起预处理,最后 \(\log\log n\) 位的暴力即可。
如果要考虑倍增,再结合对这个唯一性质的良好描述,就很容易解决这个问题。
-
T4
一直磕 T3,完全没动过 T4,失策。综合评估本题是我的能力范围内的。
首先我们利用期望的线性性拆成若干个虫子分开计算。考虑刻画一个虫子是否能吃,我们发现,只要满足以下条件,虫子 \(u\) 就能吃掉虫子 \(a_u\),下设 \(i<j\) 当且仅当 \(i\) 的行动早于 \(j\),即 \(i\) 在行动序列中比 \(j\) 靠前。
-
\(a_u<u\)
-
\(\forall v\text{ s.t. }(a_v=a_u\land a_u<v),u<v\)
换言之,比 \(a_u\) 行动晚(否则条件一都不满足)且吃 \(a_u\) 的虫子 \(v\) 都晚于 \(u\) 行动,避免 \(a_u\) 提前被 \(v\) 吃掉
-
\(a_u\) 不能吃 \(a_{a_u}\)
因此这是一个递归的条件,我们刻画出这条递归链,记 \(i\to j\) 当前仅当 \(a_i=j\),同时称 \(j\) 是 \(i\) 的后继。考虑 \(b_0=u\to b_1\to \dots\to b_k\),若 \(b_k\) 不满足条件一、二,那么我们不用再递归下去,一个方案一定对应了一条这样的链(不可能都能吃),因此我们考虑按这条链来计数。如果 \(2\nmid k\),举个例子,如果 \(k=3\),那么 \(b_3\) 不能吃,\(b_2\) 就可以吃(条件三也满足了),\(b_1\) 就不能吃(条件三不满足),\(u\) 就可以吃。
考虑到确定 \(u\) 之后这条链的可能的最多元素组成就已经固定了(当然,这条链最后一定会变成一个 \(\rho\) 的形状,但是不需要关心,断开即可,因为它显然不能吃,不可能满足条件一,其他元素至少还有可能满足条件一、二)。
那么我们称一个元素 \(b_i\) 合法当且仅当它满足前两个条件,这条链实际上的结尾、即第一个不合法 的 \(b_k\) 中的 \(k\) 为链的长度(也就是说,不算 \(u\))。那么链的长度为 \(k\) 的方案(也即是 \(b_{0\sim k-1}\) 合法,\(b_k\) 不合法)可以由链的长度大于 \(k-1\) (也就是说,\(b_{0\sim k-1}\) 都合法)的减去链的长度大于 \(k\) (也就是说,\(b_{0\sim k}\) 都合法)的来得出。那么也即是,求链的长度大于 \(l\) 的方案数 \(f_l\) 即可,当前确定的 \(u\) 的贡献就是 \(\sum_{2\nmid k}f_k - \sum_{2\mid k}f_k\)。
我们现在假定枚举了 \(u\),如何计算 \(f_m\)?
考虑问题转化为,有 \(m+2\) 个特殊小球(代表 \(m+1\) 个链上的元素和一个链的结尾的后继),另外有 \(m+1\) 种颜色(代表 \(m+1\) 个链上元素所吃的那个虫子),从 \(2\sim m+2\) 编号,有 \(c_i\) 个漆成颜色 \(i\) 的普通小球(代表其他的与链上某点吃同一虫子的虫子们),求有多少方案,任意排列小球,使得对于 \(1<i\le m+2\),第 \(i\) 个特殊小球和第 \(i-1\) 个特殊小球之间不存在漆成颜色 \(i\) 的普通小球。
考虑容斥,这 \(m+1\) 个条件是独立的,则钦定两个特殊小球之间放了 \(d_i\) 个颜色 \(i\) 的普通小球,容斥系数 \(\prod (-1)^{d_i}=(-1)^{\sum d_i}\)。我们一个一个增长链,那么我们还需将 \(\sum d_i\) 加入 DP 状态(存疑,我怀疑官解错了,其实不需要记录,否则每次背包合并复杂度就错了)。对于一个枚举的 \(u\), DP 是 \(O(n\sum c_i)\),那么总复杂度为 \(O(n^3)\)。
-
P10052 [CCO 2022] Double Attendance
最开始是想避免掉设时间的,但是不设时间的话转移只能做到 \(O(N^2)\),很麻烦,因为不能只决定最后一步。所以最后还是得设时间,此时可以使用一个非常非常常用的技巧,可以交换答案维度和状态维度,由于贪心成立可以导出最优子结构,DP 仍然有效。
20251015
都是啥鬼题,我是 FST 大王。
-
T1:没注意 0 没逆元。FST 了。
-
T2:两个语句写反。FST 了。
问题是,本题实际上可以有一个相对简单很多的正解,这样我们就有更多时间跳出 T3 的错误……
是这样,因为 \(\log^2 n\) 的做法是一眼的,但是如果你考虑优化这个做法,那么可能会绕一圈。考虑本质上就是要求出跨越正负的交点的位置,两个都是递减的,没办法直接二分(虽然我,通过诡谲手段成功二分了,但是非常复杂),这个要求跨越正负是很烦的,考虑将其中一边取相反数,我们发现,取那些取反的数就等于不选这些,因此我们要不选较小的数,选择较大的数,不选较小的数在取反之后和选择较大的数是同一个含义,可以直接线段树二分做。
-
T3:差一个逻辑问题没调出来。
-
T4:题面疑似有误,不知道怎么做。
P11927 [PA 2025] 重金属 / Heavy Metal
考虑我们可以直接在 bfs 之类的上面记录一维的当前系数这个信息,
但是这个系数太大了,虽然可能经过的非 1 边的数量可能不多只有 log,
但是这个系数是不可避免的。
考虑 meet in the middle,反向求的时候只是求可行性,
反向求的时候我们考虑已经确定了前半段,考虑
设 f_{x,i} 表示从 n 走到 x 放大系数为 i 时中间经过的最强限制
最大的是多少,这个是否能被求出来?
转移 f_{x,i} --w--> f_{v,iw}=max(f{v,iw},min(lim_v,f{x,i}/w))
考虑 f_{x,i} 不包含 x 的限制,那么
变成 f_{v,iw}=max(f_{v,iw},min(lim_x,f{x,i})/w)
那么我们可以尝试 SPFA 来暴力松弛。
假设求出来了,现在怎么合并?考虑每个点处
使用双指针即可,不过,这个 SPFA 并不是什么很确定的复杂度,但是
最多也就 NM。这样有可能通不过,但是注意到
如果 f{x,i} 超过 lim_x 之后,就没必要再尝试更新很多次,
因为出边的权值不会再改变
对了!大部分都正确,但是题解指出可以使用 Dijkstra 来替换 SPFA
这个正确吗,好像挺对。
比较简单,但是如果不是看到标签是 meet-in-middle,我能不能想出来是存疑的。
还有一点就是什么样的有环 DP 可以用 Dijkstra 做,什么样的必须用 SPFA。那么,什么样的可以用 Dijkstra 呢?我们考虑如果 \(S\to T\) 是一条使得 \(f_T\) 取得最优解的路径,只要这样的最优路径上,\(f\) 的值都是单调不优的即可。进一步地,只要对于每个点都存在一条即可。(Unsure)。具体的证明就是考虑如果马上要出队 \(T\) 了,但是从 \(S\to T\) 的最优路径上还存在某个前驱没有出队,那么就违背了上述性质。
本题的转移式显然满足此性质。
P11664 [JOI 2025 Final] 缆车 / Mi Teleferico
这一类问题都有通用的方法,这一类合法区间满足区间包含单调性的问题都可以考虑扫描线左端点,则最小合法区间的右端点递增,容易双指针求解,然后对于这个问题我们容易列出合法的条件,考虑把所有变量都放在一起,凑上常数把常数提取出来,和变量分开,最后转化成一个 RMQ 问题。
这个思路到最后已经是非常混乱的了,我显然是知道区间包含单调性的,但是没有想过用区间包含单调性扫描线,所以我觉得这个性质没用,也没有重视,但是这个思路我只能说肯定见过不止一次。
20251016
P11203 [JOIG 2024] Infection Simulation
- 不可能两个区间合并了,而被他们的并包含的区间却没与他们合并
- 一个区间,若被另一区间所包含,那么在它有机会和别人
合并之前必然先和大区间合并
不对不对,反了,但是问题不大,再看看
首先,第二点是正确的。第一点是错误的。
第一点可以改成,包含两个区间的交的区间必然先合并
这个是显然的,但是加上第二点,可以导出原先的结论。
因此两个结论都正确,第一个结论说明,一个连通块
内不可能有没有合并的区间,连通块应该形如一个大区间。
结论二说明,被包含的区间之间是不用考虑合并不合并的,
也不会存在两个极大区间被非极大区间连通的情况,
因此我们随便给非极大区间分配一个包含它的极大区间即可,
对于极大区间,使用性质一,我们只需要考虑
相邻两个极大区间的交就行,这个我们直接维护就可以了。
这下我们使用并查集即可。
我觉得应该坚持我是对的,我写一下。
不对,饭堂了,这个建模就不对,有的人虽然和
患者呆了很长时间,但是那个时候这个患者还没染病呢!
能不能改一下,前向传播是不允许的,向患者出现后传递
是 OK 的,但是向患者出现前传递,只能由患者自己进行。
l
l>=L,我们考虑启发式合并,用一个其他结构维护一个块内的
l>=L 的点。然后查询所有 l
考虑用主席树实现
我得到题解的性质了,但是我最开始饭堂了,以为边是双向的,所以整了个并查集来维护,结果后来发现那些出现于感染者前的人要感染只可能被感染者传染,他们互相不能人传人,所以急忙打上补丁,整了个线段树合并和主席树来补救,复杂度也是对的,但是常数肯定大,而且巨难写,想加写加调花了 3h。其实如果我最开始发现它向后的边都是单向的,那么我也可以尝试用倍增做,但是,本质上我的并查集就是在维护感染区间,所以说其实我本来也可以在发现错误之后把我拿到的并查集区间给下界设成 \(L_P\) 来拿到感染区间,然后就像题解的第二部分一样做就可以了。
怎么好几次都是最开始饭堂,然后整个都错了,像这种能补救的情况还是不多的。
20251017
P11114 [ROI 2024] 小推车 (Day 1)
k<=m,这个东西保证了有解性
因为瓶子不能卸下来,我们优先以瓶子作为关注对象
其实要装哪些饮料是确定的,要不然有可能遇到没办法卸下瓶子的尴尬情况
如果还有空间,
我们就按顺序找到下一个还没有满足的人,然后为他装上一瓶他要的饮料,
然后把后续 p-1 个需要这个饮料的人都标记为已经满足
这样我们永远不会遇到没法卸下瓶子这种情况,
而且可以认为这样是最优的,没必要留空位,因为
这样一定可行,在可行的情况下不留空位显然不劣
现在唯一需要决策的就是,可以在中途,也就是没有
遇到第一个没法满足的人的时候就回去,也就是主动回去
或许能减少走路的距离。
这样,如果我们要 DP,我们只需要记录上一个回去的位置,
我们可以推算出当前人是否能被当前载的饮料满足。
真的吗?这样似乎比较复杂,因为推算饮料本身就是一个复杂的过程。
<RESTART POINT>
我们根据以上策略很容易知道需要哪些饮料、在哪里需要
我们把每瓶饮料按照第一个需要它的人来排序,这瓶饮料
必须在这个位置之前被装到车上,显然每一时刻,
车上有的饮料都是这个序列的一个区间。
我们只需要知道上一次装车的时间就可以知道上一次装车后
车上有哪些饮料,就可以知道是否需要再次回去装车。
我们把每瓶饮料看成区间,左端点就是第一个需要它的人,
右端点就是最后一个使用它的人(如没用完,为 n+1)
令 f_i 表示 <=i 的都满足了,且在服务了 i 之后立刻回去装车了。
那么查看转移 j -> i,
如果一个区间左端点 <=j 右端点 >j,那么
这个饮料在装车时还在车上,剩余的空间可以用来装
左端点 >j 的一些饮料,如果空间不足以装下左端点 <i >j
的所有饮料,那么这个转移不合法,因为中途必须再次回去装车,
否则就可以转移。
因此,考虑可转移区间应该是一个区间,
并且考虑区间的端点不降。
看到题解在单调队列,估计很接近了,我们也可以
不用单调队列,管他呢,现在的硬件难道还过不去 1e6 1log?
考虑下转移区间怎么求解,
我们只需要维护两个变量就可以知道当前点可不可以转移了
全程用时约 2.5h。ROI 的样例好强,过样例就过题了。
P11519 [CCO 2024] Telephone Plans
用时约 2.5~3h。
P11352 [NOISG 2024 Finals] Coin
md,提示 1、2、3 不都是显然的吗
看题解。考虑我最开始的那个错误思路,这个错误思路就 TM 是这个结论。。。。
cnmd。竟然想不起来?????
我觉得很怪异。一般我的思路就是一路走,我几乎没有回溯的习惯,也没有这方面的经验,事实上本题全部的性质和转化我都做了,我最开始的错误做法虽然错误,但是这个性质是正确的,后来转化之后其实就变成那个错误做法尝试解决的问题,但是我根本没想起来可以用之前那个错误做法来解决。
在有向无环图中,一个点可以被其他所有点到达当且仅当图中只有它一个点的出度为 \(0\)。
20251020
-
T1/T2 略
-
T3 注意字典序的排名是倒序的、去重的排名,为什么答案是 \(O(N)\) 的呢,因为对于一个 \(l\),\([l,r]\) 的排名关于 \(r\) 严格递减,\([l,r]\) 的权值非严格递增,因此只可能存在 \(1\) 个合法答案。那么现在的问题就是如何快速求 \([l,r]\) 的排名。
最开始没做出来是因为我没理解他是去重的排名,考虑如果目标的 \(l\) 在 SA 上 \(rk(l)\),那么对于那些在 \(i>rk(l)\) 的子串,除非它是 \([l,r]\) 的真前缀,那么就不小于 \([l,r]\),可以直接计入(我最开始没领会到去重,所以不知道怎么去掉真前缀),然后还有一种情况,就是 \(i<rk(l)\),但是 \([i,n]\) 和 \([l,n]\) 的 LCP 不小于 \(r-l+1\),那么以 \(i\) 为左端点的所有子串也都不小于 \([l,r]\),同样 \([l,r]\) 的真前缀除外。那么我们需要求解一个 \(L\),满足 \(l\) 是最小的满足 \(\operatorname{LCP}(L,l)\ge r-l+1\) 的,然后求所有 \([sa(i),n],i\ge L\) 的本质不同前缀数量 \(S\),接着减掉 \(r-l\),也就是真前缀数量。那么前面这个 \(S\) 显然应该为排名 \(\ge L\) 的所有后缀的长度和减掉这一段的 \(height\) 之和,我们二分求 \(L\) 就行。
其实真的没那么难,但是我可能不会写 SA 了。而且 T2 做很久+没注意今天考试时间较短,根本没时间想。
然而注意到这玩意是 8 级知识点,是可以考的。
-
T4 没会
P14256 平局
[SWITCHER]
A. 继续考虑递归结构 [COMPLEX]
B. 继续考虑区间 DP
C. 发现其他性质
[PRE] 先毙掉连续段
考虑一个数 x,和其后面第一个和他一样的数 y,由于
去掉了连续段,中间的数必然是形如另外两个数交替出现的,
那么我必然可以通过操作将中间的数删光,然后让这两个数构成平局
这中间两种数可能产生较大的那种的数量减一的贡献,然后
那么总共就是其中较大的那种的数量个。
嗯,那么我们大概可以拿到众数 -0 / -1 / -2 个。还能更多吗?
我们考虑整一个区间 DP 来算算
似乎这个猜测挺对 但是确实还能更多。
[RETURN]
[SEEK HINT] 貌似确实需要先寻找性质
考虑这样一个构造出最大值的算法
但凡存在 aba 这种情况我们就把他消掉, 这样最后必然
只剩 0 1 2 0 1 2 0 1 2 这种是平凡的
似乎非常非常对了,只差一点点特殊情况
最后想栈是因为扫了一眼题解发现正解跟栈有关系,不然估计是想不到的。这个题最关键的是考虑要转化成差分,然后整个操作就很容易刻画了,就比较容易想到用栈了,然后可以比较自然地写出 DP,虽然说感觉这个同余的式子转化成差分已经见过几次了。
总之如果你发现你的刻画里面有任何不简洁的部分,比如有递归,比如有一些很模糊或者麻烦的条件判断,那么多半是错的,正确的刻画总是看起来相当自然。
20251021
-
T1:由于是树,连通块数等于 \(|V|-|E|\)。场上写了个给原树定向然后计算插头的算法,就是最后一个题解。
-
T2:算错复杂度了,用 Dinic 的复杂度是错误的。考虑一次二分判定等于求左边点拆成好几份然后是否存在完美匹配。考虑 Hall 定理,对于答案必须满足对于所有人的集合 \(|S|\le |N(S)|\),考虑每份左部点向右边连边都是一样的,因此只要 \(S\) 包含了某种点 \(\{x\}\) 的其中一个那么 \(N(\{x\})\subseteq N(S)\),因此没有必要拆点,那么答案就是 \(\min_{S} N(S)/S\),求 \(N(S)\) 可以用倍增加
bitset。另外,网络流加二分是可以过的(虽然直接计算网络流的复杂度是错误的,但是网络流的复杂度,你懂的),但是不能用主席树,常数飞起来了。当时写的是增量网络流,这个东西是错的,在此处实际复杂度是 \(\mathcal O(f|E|)\),\(f\) 为最大流。啊沟槽的出题人出网络流。
-
T3:其实没那么难,赛后自己想出来了。
左闭右开的 设 S(x) 表示大小为 x 的集合的集合,L(x) 表示最小的大小为 x 的集合的 权值,R(x) 同理。 显然 L(x)<=L(x+1) R(x)<=R(x+1) 我们考虑 L,R 是比较有规律的,所以考虑画到一个序列上面 我们注意到在某个位置 p 以前,一直都存在 R(x)>=L(x+1),然后某个位置之后就不存在这种情况了(然而也不可能小于 L(x)) 所以在这一段之前,全部数都是坏的,在这之后,每个区间就是相离的了。 则之后的是 rsum_i-sum_i。 那好像也没那么难,到底哪里有错呢? 确实有问题,但是大体是正确的,这两个函数一个上凸(L(x)) 一个下凸(R(x-1)) 找到两个交点即可维护。 因为两个函数是中心对称过去的,这两个函数的差不仅是凸的 而且是轴对称的,所以可以确定交点必然分属中点两侧。
P12761 [POI 2018 R2] 列车员 Conductor
太简单了。
20251023
P9758 [COCI 2022/2023 #3] Baltazar
求出最短路图和次短路图然后定向求 DAG 必经边或者直接跑 tarjan 都行。不知道为啥高赞那么复杂。
P9004 [RC-07] Abnormal Permutation Tuples
为什么要那么想呢?
什么叫没有前途的思路呢?
一个小时没有实质进展你不该反思一下吗?
我也不知道。
我也不知道这种事情什么时候为止。
或许与别人的比较只有在死后才会停止。至少这样你就听不到了,对吧。
20251022~20251023 计数专题
我恨计数。做出恨意,做到呕吐。
20251024
-
T1:做了超级久(2.5h)才做出来。别问我为什么,问就是菜,问就是脑子不好使,问就是思维惯性大。
-
T2:唐诗题卡精度。但是有一点值得记录一下,那就是
long double的 max 是 \(10^{4000}\),但是有效数字只有 \(33\) 位。 -
T3:多重背包的复杂度没法优化,必须一个元素一个元素加(二进制分组那些在这里不考虑),如果是完全背包就很好了,一个 Trick 是考虑把判定问题做成计数问题,这样用容斥就可以把多重背包的限制去掉。再者强制在线加点这种操作线段树是没法维护的,考虑根号个操作定期重构(操作分块)即可。当然写平衡树也行,但是这个可能没有操作分块好写。场上无人调出。
-
T4:这个题目很有教育意义,它告诉了我们,应该怎么找出”有用“的组合意义,而前提是认清什么样的组合意义是有用的。
平凡的想法是记录前缀信息进行 DP,但是,我们没办法避免 \(2^n\) 次方的信息,无论记录什么。那么组合意义是用来干嘛的呢?通过它你能发现原式中隐藏的性质,从而简化运算。
我们发现计算困难的根本原因是前缀信息无法避开,我们猜测肯定有一个性质让我们避开维护前缀信息。于是我们要将原式使用组合意义转化,那么关键点就是对前缀信息开刀,你不能转化完还有前缀信息。
坏的转化:
有多堆球,每堆有若干个,现在 n 个,
先随机从第一堆选,然后从前两堆随机选,然后从前三堆……好的转化:
前缀和乘积是什么意义?考虑往基本问题里面套。
有 \(\sum a_i\) 个球,其中第 \(i\) 种颜色的球有 \(a_i\) 个,且同种颜色的球之间彼此不可区分。我们要将它们排成一排。然后我们发现这个倒数很像概率或者比例,那么我们考虑当前已经插入了 \(s_i\) 个元素的情况下,\(\frac{1}{s_i}\) 可能是什么比例,显然这个比例是形如 \(\frac{a}{cnt}\),其中 \(cnt\) 表示当前有多少种排列。那么 \(cnt={s_{i}\choose a_i}\) 那么 \(a=\frac{cnt}{s_i}=\frac{1}{a_i}{s_i-1\choose a_i-1}\),则 \(M=\frac{1}{s_i}=\frac{\frac{1}{a_i}{s_i-1\choose a_i-1}}{s_i}\),\(\frac{1}{a_i}\) 不容易处理,我们将 \(M\) 乘上 \(a_i\),令 \(N=a_iM\),则存在 \(N=\frac{a_ia}{cnt}=\frac{{s_i-1\choose a_j-1}}{cnt}\),那么 \(N\) 当前的组合意义就变成我们可以随便固定一个颜色为 \(i\) 的球得到的方案占全部方案的比例,或者说概率。为了简便起见,我们固定颜色为 \(i\) 的最后一个球在 \(s_i\) 的位置(也就是当前的最后一个位置)。
那么,在这种情况下,设 \(g(a)=f(a)\prod a_i\) 的意义就显然变成,设 \(r_i\) 为最靠右的颜色为 \(i\) 的球的位置,那么考察满足 \(r_i\) 递增的排列方法的个数,这些排列占全部排列的比例就是 \(g(a)\)。
那么它究竟有什么用呢?现在它不就和排列信息无关了吗?那么我们考虑现在添上了一个 \(\prod a_i\) 的项,我们回到原问题,我们把同一个 \(a_i\) 的集合 \(A=\{a_i\}\subseteq \{1,2,\dots,m\},|A|=n\) 所构成的全部排列拿出来看,因为这一部分后面添的这个值是一样的。我们发现任何一个序列,都存在一个 \(r\) 的序列,这恰好会对 \(A\) 的某个排列造成贡献,那么 \(A\) 中全部排列的 \(g\) 值加起来就是 \(1\),因为加入小球的顺序不影响方案数,而所有方案都会对某个排列造成贡献。
而 \(\prod a_i\) 是相同的此时我们就成功转化掉全部的 \(s_i\)。
我们就展示了如何构造出一个合用的组合意义。
考虑 \(k=2\)。考虑先确定 \(a_1\)。那么现在 \(g\) 的和不一定是 \(1\) 了,而是所有 \(r_1\) 是其 \(r\) 中最小值的那些排列除以总排列数,最后再除掉刚才那个乘积。然后计算 \(r_1\) 是最小值的方案数可采用容斥。然后枚举 \(a_1\) 并 DP。
然后最后这个优化还没懂。
20251027
-
T1、T2 略
-
T3:场上没想清楚,最开始想贪心,但是没想到每次修改的时候可以维护贪心,然后后来想到可以每次维护,结果又把它变成了一种复杂的操作,最后才想到直接维护贪心就可以了。
-
T4:思维难度不大。等差数列小性质,然后加上同端点区间 \(\gcd\) 的变化次数结论。然后就是一个之前做过的求有多少数值连续的子区间这种问题,线段树上维护 \(\max-\min=(r-l)\gcd\),即可。比较难写。
不要去磕一些结构很复杂的东西。如果这个结构你磕 20min,然后就发现脑子糊了,那肯定是有问题的。
20251029
邻项交换
邻项交换引理
如果对于 \(n\) 个待确定顺序的元素 \(x\in E\),令 \(F(a_1,a_2,...,a_n)\) 为目标函数,如果存在关系 \(<_E\) 满足它是一个严格弱序,并且 \(p<_E q \implies F(a_1,a_2,...,p,q,....,a_n)< F(a_1,a_2,...,q,p,...,a_n)\) 且 \(p\not\gtrless_E q \implies F(a_1,a_2,...,p,q,....,a_n)=F(a_1,a_2,...,q,p,...,a_n)\)(注意比较 F 的关系并不是 \(<_E\)),则按照 \(<_E\) 排序能最小化 \(F\)。
证明考虑从任何一个序列应用冒泡排序一定能得到一个排序好的序列并且目标函数步步不增,在一个有下界的空间中这样做必然达到最小值。
因此,如果问题的本质是排序,那么我们通常需要找到这样的 \(<_E\)。
我们常用的手段,也就是大部分人了解的“邻项交换”,用上面的定理描述如下:
当对于目标函数 \(F\),交换相邻元素对于 \(F\) 的变化可以只用 \(p,q\) 确定时,可以应用下列方法:取出相邻元素 \(p,q\),记 \(p<_E q\) 当且仅当 “\(p\) 在 \(q\) 前严格优于 \(q\) 在 \(p\) 前”。则这个 \(<_E\) 往往满足上述引理的要求,因为大部分时候你都能得到严格弱序,而 \(F\) 的交换不劣性由 \(<_E\) 的定义保证,用这个序进行排序可以得到最优排列。
严格弱序需要满足如下条件:
-
非自反,\(x\nless_E x\)。
-
非对称,\(x<_E y\implies y\nless_E x\)。否则就代表着“怎么交换都更优”,不能确定一个顺序。我们经常忽略这一点,直接把
cmp函数中的 \(\le\) 改成 \(<\),不是因为它不重要,而是我们默认了下一条性质成立…… -
不可比的传递性,\(x\not\gtrless_E y,y\not\gtrless_E z\implies x\not\gtrless_E z\)。这是什么意思?在这里,我们说 \(x\) 与 \(y\) 不可比,想表达的是,这两个谁放前面都一样优,没有那个比那个优。那么这可以看作一种等价关系,我们称为 \(x\equiv_E y\)。如果这种关系不可传递,也就意味着,可能存在 \(x\equiv_E y,y\equiv_E z\),但是实际上存在 \(x\nless_E z\) 这种,那么此时 \(F(y,z,x)<F(x,y,z)=F(y,x,z)\),因此 \(x,y,z\) 不一定是最优的,\(y,z,x\) 才是。如果存在这种情况,虽然存在最优的顺序,但是排序算法诸如
std::sort是不能求出最优顺序的(具名要求Compare)。 -
传递性,\(x<_E y,y<_E z\implies x<_E z\)。如果不满足这个性质,说明该问题的结构比较复杂,其本质不是排序,不存在一个最优的顺序,不能是用邻项交换法。
你说的对,但是对于下列题目不适用
CF2055E Haystacks
本题中直接交换导出的 \(<_E\) 没有不可比的传递性。
但是,它是形如这种东西:\(\min(a_1,b_2)<\min(a_2,b_1)\)。
对于这种式子我们有一个通用的方法,我们考虑先分讨每种情况:
-
\(a_1<b_1,a_2=b_2\),我们发现 \(<\) 总是成立,因此在这两者之间不存在不可比的情况,\((a_1,b_1)\) 总是排在前面。
-
\(a_1>b_1,a_2=b_2\),我们发现 \(>\) 总是成立,因此同上,\((a_1,b_1)\) 总是排在后面。
-
\(a_1=b_1,a_2=b_2\),我们发现 \(\not\gtrless\) 总是成立,因此这部分满足不可比的传递性。
-
\(a_1<b_1,a_2>b_2\),\(<\) 总是成立。
-
\(a_1<b_1,a_2<b_2\),我们发现上述条件等价于 \(a_1<a_2\),也满足不可比的传递性。
-
\(a_1>b_1,a_2>b_2\),也是。
那么问题其实就出在,你比较 \((a,b),(c,d),(e,f)\),但是当 \(c=d\) 的时候可能有反例。反例见 浅谈邻项交换排序的应用以及需要注意的问题 - ouuan的博客。那么虽然顺序存在,但是如果 std::sort 不巧遇到了错误的顺序,那么就无法归位这种情况,此时我们将上面的讨论过程总结一下,帮 std::sort 一把,让它在满足不可比传递性的段内排序。
Johnson 法则
令
\[d_i=\begin{cases}-1 & a_1<b_1\\0 & a_1=b_1\\ 1 & a_1>b_1\end{cases} \]先按照 \(d_i\) 排序,对于 \(d_i\) 相同的按照 \(\min(a_1,b_2)<\min(a_2,b_1)\) 排序,即可。
本质上讲: 修复这种问题的策略就是,为 \(<_E\) 附加一个额外的规则,使得在满足传递性的前提下满足不可比的传递性,拯救排序算法。
对于如何观察出一个确定排列的答案式,我只能说多练 _
事实证明,我没有聪明到能做出此题。
20251030
解耦合
通常来说我们应该尽可能保持思维空间的简单性,Keep it simple and stupid。当我们找到性质的时候,不要急着将他们全都应用在思路上,因为:
-
可能你的性质是错误的,如果是这种情况,那就很危险
-
可能它并没有什么用,却给问题对象的形式施加了额外的限制,使得你的思考受到干扰
在描述限制条件的时候,最好将它们分类陈列,且尽可能进行形式化的表述,写出几个关键变量并用简洁而精确的语言描述。这样可以避免带着很多限制一起思考。并且写成变量形式,其实是为你之后的思考构造了工具,你可以观察这些变量的变化情况来推进思考。
如果能在全局层面考虑就尽量在全局层面考虑,因为在局部情况考虑必须满足这个局部情况与全局是隔离的,否则就必须瞻前顾后,很麻烦。
P11234 [CSP-S 2024] 擂台游戏
我觉得最清楚,最容易的理解方式如下。
首先树会扩张,这个太难了,我们不妨枚举所有可能大小,也是正确的,下称当前枚举的树的大小为 \(s\)。
考虑刻画一个人被打败的条件。我们发现,主要由两个部分组成:
-
它作为擂主时,能力值不足。假如此人尚未确定能力值,则它不受本条件限制。
-
它不作为擂主时,由于自由选手可以任意赋值,如果对面胜者是任意的,我们显然能故意让任意选手恰好输掉。因此条件是对面的胜者已经确定,并且这个胜者的能力值足够。无论此人是否已经确定,它都要受到本条件限制。
条件一是容易的,我们提前就能预处理出来某个人它最多应付多大的 \(s\)(也就是 \(s\) 再扩大,他的能力值就不足以守擂了)。这是线性的。
那么条件二怎么办呢?我们发现这个条件有两个部分,第一,对面胜者要确定;第二,对面确定的胜者能力值足够。显然,随着确定的人越来越多,一个子树必然在某个时刻转为确定,然后一直保持确定。因此,我们处理出 \(t_x\) 表示子树 \(x\) 转为确定的时刻(若子树永远不会被确定,称 \(t_x=\infty\)),\(f_x\) 表示子树 \(x\) 确定后的胜者能力值。换言之,在 \(t_x\) 及以后,除 \(f_x\) 之外,其他任何人,无论是否确定了能力值,都一定会被打败,但是若 \(t_x\neq\infty\),那么 \(f_x\) 必然是一个输入了能力值的人,并且在 \(t_x\) 时刻之前已经确定。
在某时刻 \(T\),让我们来判断某人 \(x\) 是否能胜利:
-
若此人没有确定,则所有 \(x\) 的祖先都必须还没确定,即 \(T<\min_{x\in subtree(a)} t_a\)。
-
若此人确定了,则所有 \(x\) 的祖先 \(u\),如果满足 \(x\) 在尝试走到 \(u\) 的时候不是擂主,并且它兄弟要么没有确定,要么能力值不够。也就是 \(T\) 必须小于所有 \(x\) 不是擂主时的、\(f_u\) 足够的兄弟 \(u\) 的 \(t_u\)。
上述两点,我们先 DP 求出 \(f,t\) 之后再从上向下 DP 并维护上述两个值,在叶子上我们可以进行差分来统计答案。线性解决。
- 下午模拟赛 T4:多源多汇问题的一个常见处理方式是建立超级源或超级汇点。别忘了还有圆方树这个东西,在某些关于割点和连通性的问题中很有用。
20251031
P4492 [HAOI2018] 苹果树
#include<bits/stdc++.h>
using namespace std;
const int N=2005;
typedef long long ll;
ll n,P,f[N],g[N],C[N][N];
int main(){
cin>>n>>P;
C[0][0]=1;
for(int i=1;i<=n;i++){
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=(C[i-1][j-1]+C[i-1][j])%P;
}
g[0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<=i-1;j++){
ll var=(g[j]*f[i-1-j]%P+g[i-1-j]*f[j]%P)%P;
var=(var+g[j]*g[i-1-j]%P*(n-i)%P*i%P)%P;
f[i]=(f[i]+var*C[i-1][j]%P)%P;
g[i]=(g[i]+g[j]*g[i-1-j]%P*C[i-1][j]%P)%P;
}
}
cout<<(f[n]%P+P)%P;
}
/*FOOTNOTE
让我们考察一条边期望被贡献几次(某点到其父亲的边属于这个点)
这等于 E X(n-X) = nE(X)-E(X^2)
所以为什么要乘以 N!
考虑给一棵树分配标号的过程,首先我们将
节点从上到下从左到右取出来排成一列然后 N! 地
分配,但是这样可能不满足要求,因为我们要使得父亲标号小于儿子。
事实上就是 (siz(x)\choose siz(ls(x))) 这样全都乘起来
哦,因为第一个点有 1 种选择,第二个有 2 种……所以总数是 N!
题解都是强行计算了每条边的贡献然后求和,关键是
搞清楚分每个点去分步计算合法的树个数,当然我们也证明你不用这个
方法也可以做。就是上述代码,也即 @hgzxwzf 的题解。
*/
P10674 [MX-S1-T3] 电动力学
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
typedef long long ll;
const ll P=998244353;
ll n,m,f[N];
vector<int> e[N],rst[N];
void add(vector<int> e[N],int x,int y){
e[x].push_back(y),e[y].push_back(x);
}
int tim,dfn[N],low[N],nC,siz[N];stack<int> stk;
void Tarjan(int x){
low[x]=dfn[x]=++tim,stk.push(x);
for(int v:e[x]){
if(!dfn[v]){
Tarjan(v);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x]){
++nC;int cur;
add(rst,nC,x),siz[nC]++;
do{
cur=stk.top(),stk.pop();
add(rst,cur,nC),siz[nC]++;
}while(cur!=v);
}
}else low[x]=min(low[x],dfn[v]);
}
}
ll pw2[N],ans;
void DP(int x,int fa){
ll prod=1,sum=0;
for(int v:rst[x]){
if(v==fa) continue;
DP(v,x),prod=prod*(f[v]+1)%P,sum=(sum+f[v])%P;
}
if(x>n){
f[x]=(prod-1)*pw2[siz[x]-1]%P;
prod=(prod-1-sum)%P;
ans=(ans+prod*pw2[siz[x]-1]%P)%P;
}
else{
ans=(ans+prod)%P,f[x]=prod*2ll%P-1;
prod=(prod-1-sum)%P,ans=(ans+prod)%P;
}
}
int main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
cin>>n>>m;pw2[0]=1;
for(int i=1,u,v;i<=m;i++) cin>>u>>v,add(e,u,v);
for(int i=1;i<=n;i++) pw2[i]=pw2[i-1]*2ll%P;
nC=n,Tarjan(1),DP(1,0);
cout<<((2ll*ans%P+1)%P+P)%P;
}
/*FOOTNOTE
在同一个点双中,是否一定能够找出 x->i->y 的简单路径??
好像找不出反例,但是理论上说,如果走过一个点就删除一个点,
那么删除 x 之后如果存在割点,那么不就有可能不行吗?
算了,不研究这个,考虑固定 T 对 S 计数。
圆方树,考虑两个 T 之间经过的方点所对应的所有点都能加入 S。
那么我们现在就要统计这个,我们提前给每个点带上到根的
前缀积的一个系数即可,然后我们还需要注意两两相邻方点之间会选重复,
需要减去,从儿子拼接的时候我们也需要注意这一点,然后我们需要提前将儿子的
系数在这里中断。哎反正就是一堆细节。
其实我们不需要 0/1,因为这个连接不是你可选的,而是必须做的,
要么就不从儿子转移,要么就从儿子这里乘上权值。
为啥题解需要这些辅助数组?
整理。
f_x 表示 x 中所有集合点权并且向上延申到 x 的积。
点权:方点 2^{s_x-1} 圆点 1
若为方点,我们不能选择这个点,只能承接合并工作,
(\prod (f_v+1) - 1)*2^{s_x-1} // 不可以不选点
若为圆点,我们可以考虑选择或者不选择当前点,
2*\prod(f_v+1)-1
此时我们可以将选择当前点的答案计入总数。
嗯,怎么回事呢???
*/
提供一种比现有题解简单的 DP 方式和用到结论的证明。
首先,建立原图的圆方树,注意到如果两个圆点 \(x,y\in T\),那么在圆方树上 \(x\to y\) 路径上的所有方点对应的点双连通分量中的点都能加入 \(S\),为了证明这一点,我们需要一个观察。
观察 在一个点双连通图中,如果存在三个互异的点 \(x,y,s\),则必然存在一条从 \(x\) 到 \(y\) 的简单路径且该路径经过 \(s\)。
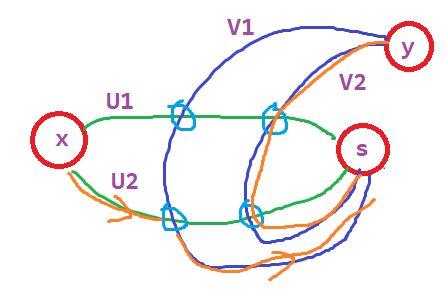
由点双连通图的性质,我们知道 \(x\to s\)、\(s\to y\) 分别存在两条不交的简单路径,我们令 \(x\to s\) 的分别为 \(U_1,U_2\),\(s\to y\) 的分别为 \(V_1,V_2\),现在我们说明,使用这些路径能构造出我们想要的路径。
假设存在一对 \(U_i,V_j\) 满足他们不交,那么选择这两条路径即可。假设这种路径对不存在,我们考虑取 \(U_2\),若将其上的点按从 \(x\) 到 \(s\) 的顺序排列,记作 \(a_1=x,a_2,a_3,\dots,a_k=s\),找到最小的 \(i\),使得 \(a_i\) 也存在于 \(V_1\) 或 \(V_2\) 上。不妨设该 \(a_i\) 存在于 \(V_1\) 上,那么我们可以知道首先 \(a_i\) 不可能存在于 \(V_2\) 上(否则 \(V_1,V_2\) 就有交点了),其次我们可以知道对于所有 \(j<i\),\(a_j\) 也不存在于 \(V_2\) 上,那么我们此时可以找到简单路径 \(x\stackrel{U_2}{\longrightarrow} a_i\stackrel{V_1}{\longrightarrow} s\stackrel{V_2}{\longrightarrow}y\),构造完成。命题得证。
有了这一观察,我们就很容易证明上述结论,对路径上进入点双和离开点双的点应用上述观察即可。
我们设圆方树上圆点 \(x\) 点权 \(v_x\) 为 \(1\),方点 \(x\) 点权 \(v_x\) 为 \(2^{s_x-1}\),其中 \(s_x\) 表示 \(x\) 这个方点所对应的点双的大小,结合上述结论容易说明集合 \(T\) 对答案的贡献就是 \(\prod_{x}v_x,\text{where }\exists a,b\in T,x\in\operatorname{path}(a,b)\),其中 \(\operatorname{path}(a,b)\) 表示树上 \(a\) 到 \(b\) 的简单路径。
接下来,我们考虑设 \(f_i\) 表示圆方树上以第 \(i\) 个点为根的子树中,所有非空集合 \(T\cup\{i\}\) 当前对答案的贡献之和。
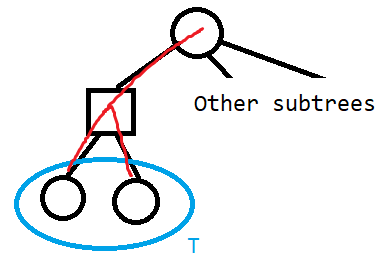
也就是提前将选 \(i\) 的权值记上了,转移分情况讨论,以下记 \(v\) 为 \(x\) 的直接儿子:
-
对于方点 \(x\),\(f_x=\left(\prod_v \left(f_v+1\right)-1\right)\times2^{s_x-1}\)
-
对于圆点 \(x\),\(f_x=2\left(\prod_v \left(f_v+1\right)-1\right)-1\)
意义非常明确,应当无需赘述。对于每个集合 \(T\),我们在其所有点的 LCA 处统计它的贡献。以下记 \(x\) 的儿子集合 \(v\in S\)。
-
对于方点 \(x\),\(ans\gets ans+\left(\sum_{P\subseteq S,|P|\ge 2}\prod_{v\in P}f_v\right)\times 2^{s_x-1}\)
说人话就是,至少选择两个子树的集合合并,保证 LCA 是 \(x\)。
-
对于圆点 \(x\),\(ans\gets ans+\prod_v \left(f_v+1\right)+\sum_{P\subseteq S,|P|\ge 2}\prod_{v\in P}f_v\)
说人话就是,如果选择这个点,那么子树随便怎么都行,如果不选 \(x\) 这个点,那么至少选择两个子树的集合来合并。
这些转移非常容易维护。最后,注意到我们给权值定义为 \(2^{s_x-1}\) 的原因是要排除相邻方点之间的割点,但是现在多排除了一个点,最后需要乘以 \(2\)。另外,\(S=T=\emptyset\) 是一种合法方案,给答案加 \(1\)。
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
typedef long long ll;
const ll P=998244353;
ll n,m,f[N];
vector<int> e[N],rst[N];
void add(vector<int> e[N],int x,int y){
e[x].push_back(y),e[y].push_back(x);
}
int tim,dfn[N],low[N],nC,siz[N];stack<int> stk;
void Tarjan(int x){
low[x]=dfn[x]=++tim,stk.push(x);
for(int v:e[x]){
if(!dfn[v]){
Tarjan(v);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x]){
++nC;int cur;
add(rst,nC,x),siz[nC]++;
do{
cur=stk.top(),stk.pop();
add(rst,cur,nC),siz[nC]++;
}while(cur!=v);
}
}else low[x]=min(low[x],dfn[v]);
}
}
ll pw2[N],ans;
void DP(int x,int fa){
ll prod=1,sum=0;
for(int v:rst[x]){
if(v==fa) continue;
DP(v,x),prod=prod*(f[v]+1)%P,sum=(sum+f[v])%P;
}
if(x>n){
f[x]=(prod-1)*pw2[siz[x]-1]%P;
prod=(prod-1-sum)%P;
ans=(ans+prod*pw2[siz[x]-1]%P)%P;
}
else{
ans=(ans+prod)%P,f[x]=prod*2ll%P-1;
prod=(prod-1-sum)%P,ans=(ans+prod)%P;
}
}
int main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
cin>>n>>m;pw2[0]=1;
for(int i=1,u,v;i<=m;i++) cin>>u>>v,add(e,u,v);
for(int i=1;i<=n;i++) pw2[i]=pw2[i-1]*2ll%P;
nC=n,Tarjan(1),DP(1,0);
cout<<((2ll*ans%P+1)%P+P)%P;
}
做完了喵!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号