树 基本操作 直通车
树
树的概念
树的定义
树是一种重要的数据结构,本质上是一种特殊的图。每一个结点可能有多个或者没有子结点,但是除了根节点外每一个节点都必须有一个父节点。因为这一个特性,点数为 \(n\) 的树会有 \(n-1\) 条边。
基本术语
- 一个结点的孩子个数叫做这个结点的度;
- 假如有一个结点 \(K\),那么结点 \(K\) 到根结点上的所有结点都叫做结点 \(K\) 的祖先;
- 结点的层次定义为根结点到当前结点的长度;
- 度为 \(0\) 的结点称之为叶子结点,度不为 \(0\) 的结点称之为分支结点;
树的存储
双亲表示法
记录每一个结点的父亲,假设第 \(i\) 个结点的父亲为 \(f_i\)。这种结构的好处是可以方便的从下往上进行遍历,并且占用空间小,但是由于只记录了父亲,因此很多操作都无法完成,只能在特定的环境下使用。比如并查集。
邻接矩阵
如果这棵树没有边权,那么我们就使用一个数组 \(f\) 来记录,如果 \(f_{(i,j)}\) 为 \(1\),那么说明 \(i\) 到 \(j\) 有边。这种做法十分简单,但是空间十分大。树是一个稀疏图,当 \(n\) 很大的时候其实边数只有 \(n-1\),因此大多数情况也不会这样写。
邻接表
我们直接存储一个结点可以到那些结点,那么就需要 \(n\) 个动态数组,可以使用 vector 或者链表。这种存储结构是最适合树的,应用场景最广,大部分题目都可以使用邻接表来进行存储。
vector<int> e[kMaxN];
e[u].push_back(v); // u 加一条边到 v
复杂度对比
假设点的数量是 \(n\),树的高度为 \(k\)。
| 项目 | 双亲表示法 | 邻接矩阵 | 邻接表 |
|---|---|---|---|
| 空间复杂度 | \(\mathcal O(n)\) | \(\mathcal O(n^2)\) | \(\mathcal O(n)\) |
| 查询 \(u\) 到 \(j\) 是否有边 | \(\mathcal O(n)\) | \(\mathcal O(1)\) | \(\mathcal O(n)\) |
| 遍历整棵树 | \(\mathcal O(n^2)\) | \(\mathcal O(n^2)\) | \(\mathcal O(n)\) |
| 从下往上遍历 | \(\mathcal O(k)\) | \(\mathcal O(nk)\) | 原版 \(\mathcal O(nk)\),魔改版 \(\mathcal O(k)\) |
可以看出,邻接表在大部分情况下复杂度都是否优秀,所以这就是为什么邻接表会在树的存储中大受欢迎的原因。以下的程序都使用邻接表来实现的。
树的遍历
深度优先
遍历完当前结点就递归遍历所有的子结点,可以使用 dfs 实现。注意如果存了双向边的话,其实不需要开标记数组,我们可以在递归的使用使用一个变量 \(f\) 来记录当前结点的父亲,这样子就不会遍历到重复的点。
void dfs(int x, int f) {
cout << x << ' ';
for (int i : e[x]) {
if (i != f) {
dfs(i, x);
}
}
}
广度优先
每次遍历一整层,其实就是广度优先搜索,使用队列实现。
queue<pair<int, int>> q;
void Record(int lst, int f, int x) {
if (x == f) {
return;
}
q.push({x, lst});
}
void Record(int st) {
for (q.push({st, 0}); q.size(); q.pop()) {
cout << q.front().first << ' ';
for (int i : e[q.front().first]) {
Record(q.front().first, q.front().second, i);
}
}
}
简单树上问题
树的直径
定义
树的直径其实就是两点之间的最长距离。
思路
我们从根节点开始跑 dfs,可以求出根节点到任意结点的距离,然后我们挑选一个距离最远的点,从这个点开始再跑一遍 dfs,最后遍历所有的点求出最大值。这种方法适合没有负权边的树,还有一种方法是树上 dp,不过过于复杂暂时不讲。
代码
void dfs(int x, int f) {
for (auto i : e[x]) {
if (i.first != f) {
d[i.first] = d[x] + i.second;
dfs(i.first, x);
}
}
}
int main() {
cin >> n;
for (int i = 1, u, v, w; i < n; i++) {
cin >> u >> v >> w;
e[u].push_back({v, w});
e[v].push_back({u, w});
}
dfs(1, 0);
int id = max_element(d + 1, d + n + 1) - d;
fill(d + 1, d + n + 1, 0);
dfs(id, 0);
cout << *max_element(d + 1, d + n + 1) << '\n';
return 0;
}
树的重心
定义
若一个点 \(p\) 的所有儿子的 / 子树的大小 / 当中的最大值 / 小于等于 \(n\div 2\),那么 \(p\) 就是这棵树的重心。
思路
我们直接模拟这个过程。若当前点为 \(i\),那么 \(i\) 的整个子树的大小就是 \(sz_i\),儿子的子树的最大大小就是 \(mx_i\)。我们遍历邻边,递归处理之后将大小加到当前子树的大小上,然后取最大值就行了。注意一棵树的重心可能有多个,而题目中要求排序。
代码
void dfs(int x, int f) {
sz[x] = 1, mx[x] = 0;
for (int i : e[x]) {
if (i != f) {
dfs(i, x);
sz[x] += sz[i];
mx[x] = max(mx[x], sz[i]);
}
}
mx[x] = max(mx[x], n - sz[x]);
if (mx[x] <= n / 2) {
ans.push_back(x);
}
}
int main() {
cin >> n;
for (int i = 1, u, v; i < n; i++) {
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1, 0);
sort(ans.begin(), ans.end());
for_each(ans.begin(), ans.end(), [](int x) {
cout << x << ' ';
});
return 0;
}
表达式树
题目
给定一个后缀表达式,求中缀表达式。
思路
我们可以使用一个树来存储。比如 1 2 * 2 + 4 5 + * 可以看成如下的图片:
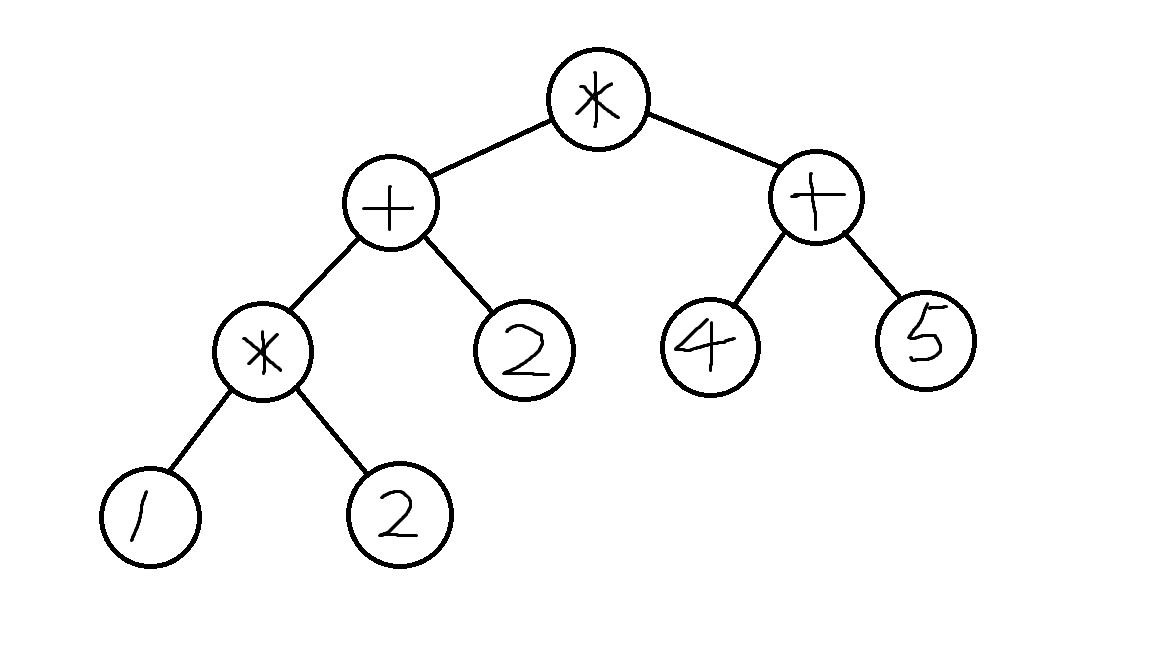
而我们只需要进行中序遍历就行了。至于如何建立这棵树——每一次的操作都对应了两个操作数,因此使用一个简简单单的栈结构就行了。
代码
#include <iostream>
#include <vector>
using namespace std;
struct Node {
int l, r, c;
Node(int l, int r, int c) : l(l), r(r), c(c) { }
};
int n, x;
char c;
vector<Node> t;
vector<int> v;
void dfs(int x) {
if (t[x].l == -1) {
cout << t[x].c;
} else {
cout << '(';
dfs(t[x].l);
cout << ' ' << char(t[x].c) << ' ';
dfs(t[x].r);
cout << ')';
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> c;
if (isdigit(c)) {
cin.putback(c) >> x;
t.push_back(Node(-1, -1, x));
v.push_back(t.size() - 1);
} else {
int r = v.back();
v.pop_back();
int l = v.back();
v.pop_back();
t.emplace_back(l, r, c);
v.push_back(t.size() - 1);
}
}
dfs(t.size() - 1);
return 0;
}
二叉树
二叉树的概念
二叉树的定义
顾名思义,二叉树就是任意一个结点最多只有 \(2\) 个儿子结点,其实也非常简单,只是多了一些特殊性质。
特殊的二叉树
斜树
所有结点都只有左儿子,就叫做左斜树;所有结点都只有右儿子,叫做右斜树。这俩玩意都统称为斜树。
满二叉树
有一颗高度为 \(k\) 的二叉树,若结点数正好为 \(2^k-1\) 个,那么这棵树就叫做满二叉树。也就是除了叶子结点的结点,每一个结点都正好有两个儿子。那么对于一个结点 \(p\),结点 \(p\) 的左儿子就可以看作 \(2\times p\),右儿子就可以看作 \(2\times p+1\),父亲就可以看作 \(\lfloor \dfrac{p}{2}\rfloor\)。
完全二叉树
假如有一颗树,每一个结点的编号都与满二叉树上的同样位置的结点对应,那么这棵树就叫做完全二叉树。
二叉树的性质
- 若结点数量为 \(n\),那么边的数量为 \(n-1\);
- 第 \(k\) 层的结点树最多有 \(2^{k-1}\) 个结点,高度为 \(k\) 的二叉树最多有 \(2^k-1\) 个结点,也就是 \(\sum\limits_{i=0}^{k-1}2^k\)。
- 假如一颗完全二叉树的结点数量为 \(n\),那么这颗完全二叉树的高度为 \(\lfloor\log_2 n\rfloor +1\)。
二叉树的遍历
遍历方法
前序遍历
每次先遍历自己,再遍历左儿子,最后遍历右儿子。
void dfs(int x) {
cout << x << ' ';
if (hasLeft(x)) {
dfs(left(x));
}
if (hasRight(x)) {
dfs(right(x));
}
}
中序遍历
先遍历左儿子,再遍历当前结点,最后遍历右儿子。
void dfs(int x) {
if (hasLeft(x)) {
dfs(left(x));
}
cout << x << ' ';
if (hasRight(x)) {
dfs(right(x));
}
}
后序遍历
先遍历左右儿子,最后遍历当前结点。
void dfs(int x) {
if (hasLeft(x)) {
dfs(left(x));
}
if (hasRight(x)) {
dfs(right(x));
}
cout << x << ' ';
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号