2023.12.13 秋季训练五
阅读 pdf,观感更上一层楼
水题环节
A - Short Sort
题目大意
有 \(3\) 张卡片,上面写着 \(\texttt{a,b,c}\),以任意排列的形式出现在一行中,你可以进行一次交换操作,问你经过操作之后,能否使这三张卡片的顺序正好变为 \(\texttt{abc}\)?
思路
这题非常简单,好渴鹅这里的写法可能代码有点长,但是思路十分简单,就是不断 swap,然后看一看是否满足要求,如果都不能满足那么就输出无解。
代码
#include <iostream>
using namespace std;
int t = 1;
char a, b, c;
void solve() {
cin >> a >> b >> c;
if (a == 'a' && b == 'b' && c == 'c') {
cout << "YES\n";
return;
}
swap(a, b);
if (a == 'a' && b == 'b' && c == 'c') {
cout << "YES\n";
return;
}
swap(a, b);
swap(a, c);
if (a == 'a' && b == 'b' && c == 'c') {
cout << "YES\n";
return;
}
swap(a, c);
swap(b, c);
if (a == 'a' && b == 'b' && c == 'c') {
cout << "YES\n";
return;
}
swap(b, c);
cout << "NO\n";
}
int main() {
for (cin >> t; t; t--) {
solve();
}
return 0;
}
C - Good Kid
题目大意
有一个长度为 \(n\) 的正整数序列 \(a\),你可以将其中的一个整数加上 \(1\),然后问你加完之后的最大乘积是多少。
\(1\le n\le 9,0\le a_i\le 9\)
思路
这道题目的数据非常非常水,我们可以枚举更改的数 \(a_i\)。对于每一个 \(i\),我们都用一个 \(\mathcal O(n)\) 的循环计算值,然后在所有 \(i\) 的答案中取上最大值即可。
代码
#include <iostream>
using namespace std;
using ll = long long;
const ll kMaxN = 1e5 + 5;
ll a[kMaxN], p[kMaxN] = {1}, t = 1, n;
void solve() {
cin >> n;
for (ll i = 1; i <= n; i++) {
cin >> a[i];
}
ll ans = 0;
for (ll i = 1; i <= n; i++) {
ll x = 1;
for (ll j = 1; j <= n; j++) {
if (j == i) {
x *= a[j] + 1;
} else {
x *= a[j];
}
}
ans = max(ans, x);
}
cout << ans << '\n';
}
int main() {
for (cin >> t; t; t--) {
solve();
}
return 0;
}
D - Target Practice
题目大意
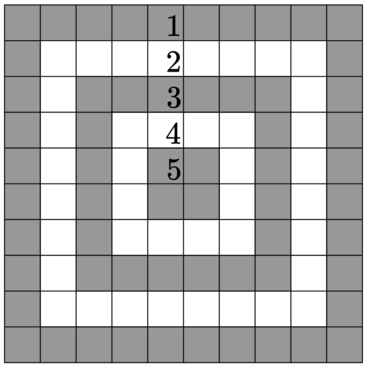
有一个 \(10\times 10\) 的靶子,告诉你了这个靶子的射箭情况,如果一个格子的值为
X,那么就说明这个格子被射到了。射到不同的格子上,分数也不相同。你需要计算总分。
思路
这题也太炸裂了吧?其实最难的部分就是如何计算一个格子是多少分。我们先枚举 \(i\),表示假设这个格子的得分为 \(i\),然后再在 \([i,n-i+1]\) 的范围内枚举 \(j\),可以在图上找到这个规律。那么如果点 \((x,y)\) 在 \((i,j),(x-i+1,j),(j,i),(j,n-i+1)\) 上,那么这个点的值就是 \(i\)。然后枚举即可。
代码
#include <iostream>
using namespace std;
using ll = long long;
const ll kMaxN = 1005;
ll t = 1, n = 10;
char a[kMaxN][kMaxN];
int calc(int x, int y) {
for (int i = 1; i <= 5; i++) {
for (int j = 1 + i - 1; j <= n - i + 1; j++) {
if (x == i && y == j) {
return i;
} else if (x == n - i + 1 && y == j) {
return i;
} else if (x == j && y == i) {
return i;
} else if (x == j && y == n - i + 1) {
return i;
}
}
}
}
void solve() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> a[i][j];
}
}
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (a[i][j] == 'X') {
ans += calc(i, j);
}
}
}
cout << ans << '\n';
}
int main() {
for (cin >> t; t; t--) {
solve();
}
return 0;
}
正常题目环节
F - 1D Eraser
题目大意
有一个长度为 \(n\) 的彩带,上面的颜色只可能是黑
B或白W。给定一个 \(k\),每一次你可以把一个长度为 \(k\) 的子序列里面的颜色全部涂成白色,问你最少需要几次才能将这条彩带全部涂成白色。
思路
我们可以想出一个贪心策略。首先我们找到第一个黑色的地方,然后将这个地方以及后面的 \(k\) 个位置全部都涂成白色,因为对于任意的一个黑色的块,越在后面的时候涂成白色,那么就有可能“事半功倍”——将几个黑色的块同时涂成了白色。
因此我们枚举 \(i\),如果 \(a_i\) 为 B,那么就将 \(i\sim i+k-1\) 内全部涂成白色。事实上,我们并不需要更改原数组,涂成白色的时候将 \(i\) 直接加上 \(k\) 就行了。
代码
#include <iostream>
using namespace std;
using ll = long long;
const ll kMaxN = 1e6 + 5;
ll t = 1, p[kMaxN], n, k;
char a[kMaxN];
void solve() {
cin >> n >> k;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
int ans = 0;
for (int i = 1; i <= n; ) {
if (a[i] == 'B') {
i += k, ans++;
} else {
i++;
}
}
cout << ans << '\n';
}
int main() {
for (cin >> t; t; t--) {
solve();
}
return 0;
}
B - Building an Aquarium
题目大意
有 \(n\) 个水箱,第 \(i\) 个水箱里面有 \(a_i\) 高的水。现在你有 \(x\) 桶水,每一桶水可以将指定的一个水箱里面的水的高度加一。问你所有水箱的最低高度最高是多少。
思路
妥妥的二分版子题,不过这里还是先讲一讲错误思路。
我们可以设计一个优先队列,堆顶就是最矮的水箱,然后遍历 \(x\) 次,每一次都将最矮的水箱里面的水的高度加一,然后操作完直接输出堆顶就行了。这种做法的时间复杂度为 \(\mathcal O(x\log_2 n)\),但是由于这题 \(x\le 10^9\),因此会直接爆掉。
我们意识到了这种做法过于依赖 \(x\) 的大小,使得了我们会超时。仔细想想,我们发现了,对于一个解 \(ans\),我们可以很轻松地在 \(\mathcal O(n)\) 的时间内判断这个解是否合法;而且我们还发现了 \(ans\) 越小,合法的概率就越高。这不就是二分吗?我们在 \([1,10^{10}]\) 内进行二分,对于一个解,如果可行就记录答案,然后尝试更大的解;否则,就往小的分。
!!! warning 注意
二分的上界不能是 \(10^9\),实际上要比 \(10^9\) 要大,极限情况下可能会达到 \(2\times 10^9\)。这里开了 \(10^{10}\),基本上不可能爆掉,但是要使用 \(64\) 位整数。
代码
#include <iostream>
using namespace std;
using ll = long long;
const ll kMaxN = 1e6 + 5;
ll a[kMaxN], t = 1, n, X, ans;
bool C(ll x) {
ll c = 0;
for (ll i = 1; i <= n; i++) {
if (a[i] < x) {
c += x - a[i];
}
}
return c <= X;
}
void solve() {
cin >> n >> X;
for (ll i = 1; i <= n; i++) {
cin >> a[i];
}
for (ll l = 1, r = 1e10; l <= r; ) {
ll m = (l + r) >> 1;
if (C(m)) {
ans = m, l = m + 1;
} else {
r = m - 1;
}
}
cout << ans << '\n';
}
int main() {
for (cin >> t; t; t--) {
solve();
}
return 0;
}
看似很♂实则很水的题目
E - Another Permutation Problem
题目大意
给定 \(n\),你需要找到一个长度为 \(n\) 的排列 \(p\),使得以下计算出来的值最大:
\[(\sum_{i=1}^{n}p_i\times i)-(\max_{j=1}^{n}p_j\times j) \]
思路
其实这题最难的部分就是找规律。我们可以设计一个测试程序,也就是 \(n\in [1,12]\) 的情况,然后使用 STL 的下一个排列函数 next_permution 枚举全排列,最后计算值就行了,并输出值最大的排列。
然后我们就可以找到规律,每一次 \(p\) 都是 \((1,2,\cdots,d,n,n-1,\cdots,d+1)\) 的形式 \((1\le d\le n)\)。因此我们尝试直接枚举 \(d\),然后用这种方法直接填充序列,最后计算值取最大就行了。
代码
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
const ll kMaxN = 25005;
ll a[kMaxN], t, n, m, ans;
int main() {
for (cin >> t; t; t--) {
cin >> n, ans = 0;
for (ll k = 1; k <= n; k++) {
for (ll i = 1; i <= n; i++) {
if (i <= n - k) {
a[i] = i;
} else {
a[n - (i - (n - k)) + 1] = i;
}
}
ll mx = 0, s = 0;
for (ll i = 1; i <= n; i++) {
mx = max(mx, a[i] * i);
s += a[i] * i;
}
ans = max(ans, s - mx);
}
cout << ans << '\n';;
}
return 0;
}
G - Olya and Game with Arrays
题目大意
给定 \(n\),有一个二维数组,第 \(i\) 行的数字数量为 \(m_i\),也就是说这个数组是以如下形式给出的。你可以从二维数组的每一个一维数组中随便挑选一个元素(最多一次),并将这个元素移动到任意一个其它数组当中,然后以一下形式计算值。问你最大的值是多少。
示例
数组:
计算方法:
思路
这题我想了很久,但是思来想去还是贪心!我们可以这样想,对于一个数组,先计算出最小值和次小值,我们肯定是要把最小的元素抛出去才是就优的吧,那我们抛到哪里去呢?我们就枚举跑抛到了哪里,然后进行计算。
那你肯定会问:这种做法是 \(\mathcal O(n^2)\) 的,不会超时吗?当然,不过我们可以用前缀和优化。将所有的最小值抛到 \(i\),那么答案就是所有的次小值的和减去 \(i\) 的次小值,再加上所有数组的最小值最小值,因为所有的最小值都抛到 \(i\) 了。
注意
这题也需要使用 \(64\) 位整数,不然会 WA。我们著名的 tyk 巨佬就因为这个原因 WA 了好几次。(事实上,他所有 WA 的题目全部都是因为
long long的原因)
代码
#include <iostream>
#include <algorithm>
using namespace std;
using ll = long long;
const ll kMaxN = 1e5 + 5;
ll a[kMaxN], b[kMaxN], e[kMaxN], p[kMaxN], f[kMaxN], t, n, m, ans;
int main() {
for (cin >> t; t; t--) {
cin >> n, ans = 0;
for (ll i = 1; i <= n; i++) {
cin >> m;
for (ll j = 1, x; j <= m; j++) {
cin >> e[j];
}
sort(e + 1, e + m + 1);
a[i] = e[1], b[i] = e[2];
f[i] = a[i];
}
if (n == 1) {
cout << a[1] << '\n';
continue;
}
for (ll i = 1; i <= n; i++) {
p[i] = p[i - 1] + b[i];
}
sort(f + 1, f + n + 1);
for (ll i = 1; i <= n; i++) { // 将最小值全部放到 i 里面
ans = max(ans, p[n] - b[i] + f[1]);
}
cout << ans << '\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号